Cours de mathématiques de 2ndeInéquations du 1er degré |
|
Video |
Texte
Une inéquation est une contrainte sur une (ou plusieurs) inconnue(s), où l'expression de la contrainte ne fait pas intervenir le signe = mais l'un des signes < ≤ ≥ ou >.
Exemple : trouver x tel que x - 2 ≥ 5.
On "trouve" x ≥ 7.
Dans cette leçon, on s'intéresse aux inéquations ne faisant intervenir qu'une seule inconnue "x", et où la ou les expressions littérales impliquant "x" sont des polynômes du 1er degré en x (ce qu'on appelle parfois des formes linéaires en x).
Exemple : ax + b < cx + d
Règles de manipulations algébriques simples.
1) si f(x) < g(x) et h(x) < k(x) (où f, g, h et k sont des fonctions quelconques) alors f(x) + h(x) < g(x) + k(x)
en particulier on peut ajouter (ou soustraire) de chaque côté d'une inéquation un même nombre c :
f(x) + c < g(x) + c
Et cette règle est vraie pour les quatre signes < ≤ ≥ ou >.
2) si f(x) < g(x) et c est un nombre positif, alors [ c fois f(x) ] < [ c fois g(x) ]. Et bien sûr on peut aussi diviser de part et d'autre par "c" sans changer le sens de l'inéquation, car diviser par "c", c'est pareil que multiplier par "1/c".
3) changement de sens si on multiplie par un nombre négatif : c'est la seule règle à laquelle il faut prêter plus spécialement attention
Si f(x) < g(x) et c < 0, alors [ c fois f(x) ] > [ c fois g(x) ]
Tableau de variation :
Regardons le signe de ax + b en fonction de x (supposons a > 0)
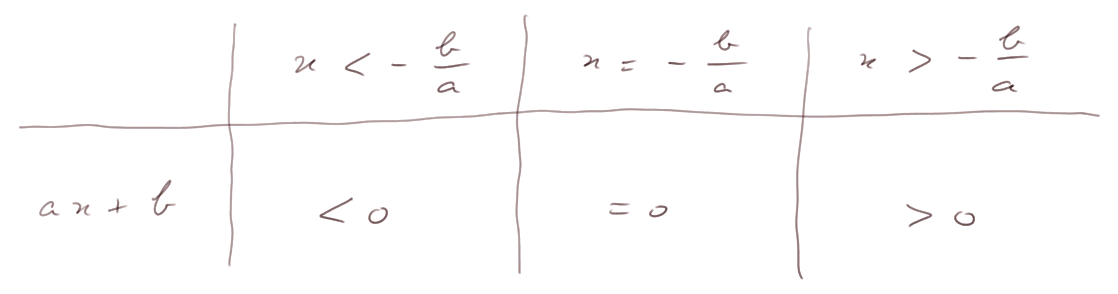
Avec ces règles on peut résoudre toutes sortes d'inéquations.
Exemple 1 : trouver x tel que 3x - 2 ≥ x + 4
un peu d'algèbre en utilisant les règles ci-dessus donne
-> 2x ≥ 6
-> x ≥ 3
Et on peut vérifier que si x = 3 les deux termes sont égaux. Si x est plus grand que 3 le terme de gauche croît plus vite que le terme de droite. Et si x est plus petit que 3 le terme de gauche décroît plus vite que le terme de droite.
Exemple 2 : (ce n'est pas à proprement parler une inéquation du 1er degré, mais ça revient au même car on va considérer des fonctions linéaires)
trouver x tel que (2x - 5)(x + 3) > 0
Ici on va faire le tableau de variation complet en tenant compte des changements de signes à x = 5/2 et à x = -3
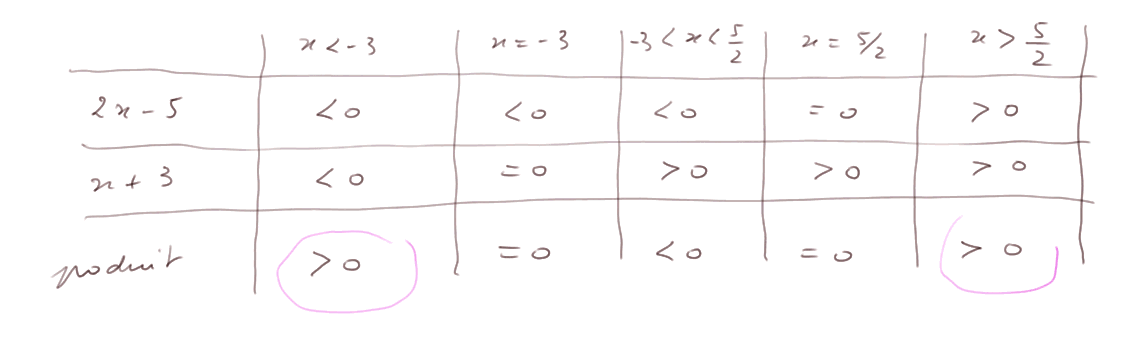
On voit que la solution est x < -3 ou x > 5/2.
On peut écrire cela : x doit appartenir à l'ensemble ] -∞ ; -3 [ ∪ ] 5/2 ; +∞ [ (où on se rappelle que ∪ veut dire "union").
Exercices :
- Trouver x tel que (2x - 4)(x - 1) < 4
- Trouver x tel que [ (1 - x ) / ( 1 + x ) ] ≤ 1