Cours de mathématiques de 2nde Les vecteurs (1) : définition, correspondance avec les translations
Video

Texte

On peut étudier les vecteurs sur une droite, dans le plan, dans l'espace, etc. Nous allons les étudier dans le plan.

Pour comprendre à la fois la simplicité et la nouveauté des vecteurs par rapport à ce que nous connaissons déjà, il est nécessaire de rappeler une notion fondamentale de mathématiques : les correspondances biunivoques.

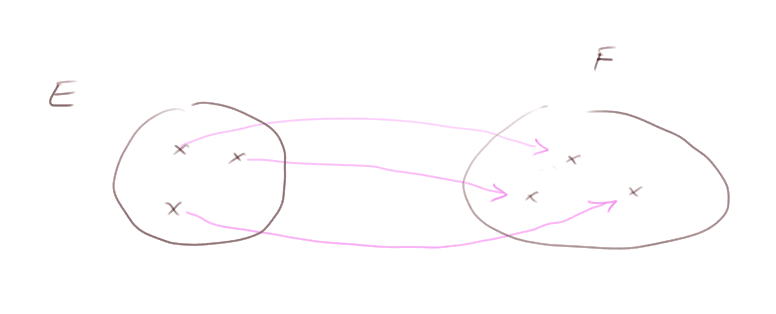
Correspondance biunivoque. Une correspondance biunivoque entre deux ensembles E et F de choses quelconques est une correspondance qui à chaque objet de E fait correspondre un objet de F, et telle que chaque objet de F est le correspondant d'un et un seul objet de E.

Exemple avec des ensembles finis :

Exemple avec des ensembles infinis : considérons l'ensemble N des entiers positifs ou nuls, { 0, 1, 2, 3, 4, 5, 6, 7...}, et le même ensemble mais où il manque les trois premiers éléments, { 3, 4, 5, 6, 7, 9, 10, 11...}. Appelons-le M.

La correspondance qui à tout élément n de N, fait correspondre n + 3, est une correspondance biunivoque entre N et M. C'est un peu bizarre une correspondance biunivoque entre un ensemble et une partie strictement plus petite de lui-même. A vrai dire, c'est la définition de ce qu'est un ensemble infini : un ensemble qui peut être mis en bijection (= correspondance biunivoque) avec une partie de lui-même.

 

Correspondance d'objets et correspondance de structures. Supposons qu'en plus de la correspondance biunivoque entre les éléments de E et les éléments de F, à certaines opérations dans E correspondent des opérations dans F, par exemple à une fonction dans E, du genre à "a + b -> c, " corresponde " a' + b' -> c' " dans F , alors les deux ensembles et leurs structures se ressemblent vraiment beaucoup.

Parfois, des résultats difficiles dans l'une des situations (des propriétés d'opérations dans E), deviennent des résultats plus faciles dans l'autre (des propriétés d'opérations correspondantes dans F). Un exemple est donné par ce qu'on appelle les "transformations par polaires réciproques" qui sont du niveau de terminale. C'est une technique courante en mathématiques et même dans la vie quotidienne.

Pour aller plus loin : voir la théorie des catégories.

 

Droite et nombres, et vecteurs et translations. De la même manière qu'avec une droite, sur laquelle on a choisi un point correspondant au nombre 0 et un point correspondant au nombre 1, il existe une correspondance biunivoque entre les nombres réels (les nombres de R) et les points de la droite, les vecteurs du plan correspondent aux translations exprimées numériquement.

 

Un peu d'abstraction. Les nombres entiers correspondent à des points de la droite de représentation des nombres, mais ils "ne sont pas" les points aux marques entières de la droite.

Les nombres entiers sont un concept plus général.

• Ils servent à compter
• Quand je compte 7 roses dans ce bouquet, je ne visualise pas automatiquement le point à la marque 7 sur la droite de représentation des nombres !

 

Vecteurs. De la même manière, dans le plan, où pour la clarté on a placé un repère quadrillé habituel, les vecteurs correspondent aux translations exprimées numériquement (du genre : "faites deux pas vers la droite et un pas vers le bas"), mais sont un concept plus général.

Exemple de translation : à tout point P on fait correspondre le point P' tel que

• abscisse de P' = abscisse de P + 3
• ordonnée de P' = ordonnée de P + 2

On peut noter cette translation T = (3, 2)

 

Exemple de translations dans le plan :

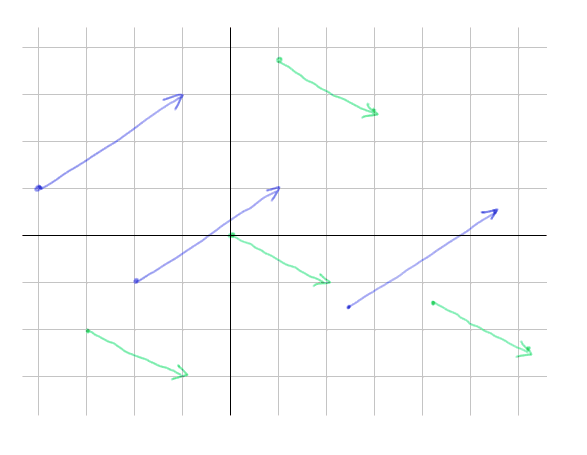
Nous avons représenté ci-dessus deux translations, chaque fois en montrant les transformés d'un certain nombre de points. La translation bleue, à tout point P, associe un point P' obtenu en se déplaçant de 3 à droite et de 2 au dessus. La translation verte, à tout point P, associe P', obtenu en se déplaçant de 2 vers la droite et de 1 vers le bas (soit -1 vers le haut).

 

Translations et points dans le plan. Il y a aussi une correspondance biunivoque entre les translations dans le plan, et les points dans le plan : à chaque translation T on associe le transformé du point (0, 0)

 

Addition des translations. Les translations s'additionnent. Si T₁ correspond à (3, 2) et T₂ correspond à (2, -1), alors on note

T₁ + T₂ = la translation T₁ appliquée après la translation T₂

Par les propriétés des parallélogrammes, on voit que T₁ + T₂ est la translation (5, 1), et l'addition des translations est commutative.

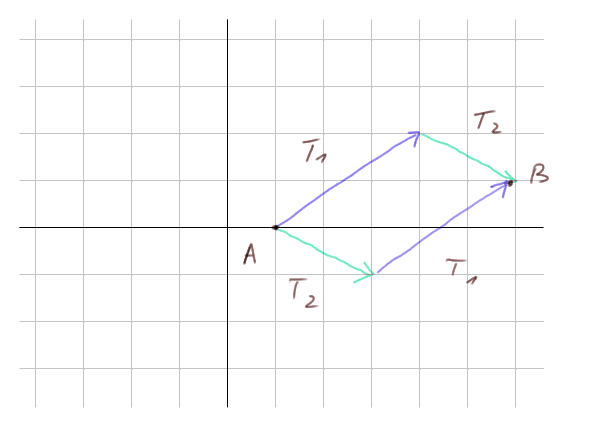
T₂ + T₁ (A) donne B avec le chemin passant par le haut. Et T₁ + T₂ (A) donne aussi B, mais avec le chemin passant par le bas.

 

Ce qu'il faut retenir de cette première leçon sur les vecteurs.

• Les vecteurs correspondent aux translations dans le plan, mais sont un concept plus général
• Comme les translations correspondent elles-mêmes aux points dans le plan (transformés de (0, 0)), les vecteurs correspondent aux points dans le plan
• Les vecteurs peuvent s'additionner (comme on combine deux translations) et l'addition est commutative

L'étude élémentaire des vecteurs dans le plan ne sera pas grand chose de plus qu'une révision des propriétés des parallélogrammes. Mais il sera important de garder à l'esprit que, de la même manière que les nombres sont un concept plus général que les points, les vecteurs sont un concept plus général que les translations.

Dans la leçon suivante, nous allons voir quelques propriétés des vecteurs, et commencer à les utiliser.

Pour ceux qui comprennent l'anglais, voici la présentation des vecteurs par le Prof. Lewin du MIT au début de son célèbre cours de physique en video pour freshman : physics 8.01 classical mechanics fall 1999 lecture 3

 

Une dernière observation :

On peut penser à un point (sur une droite, dans le plan, ou ailleurs) avant qu'on lui ait assigné un nombre. Sur une droite, pour lui assigner un nombre, il faut avoir choisi un point origine ainsi qu'une unité.

De même, les vecteurs sont des objets dans le plan (ou un espace avec plus de dimensions) avant qu'on leur ait attribué des composantes.

Et, comme un point sur une droite aura une coordonnée différente selon l'origine et l'unité choisie, un vecteur dans le plan se verra assigner deux composantes seulement après avoir choisi un point origine et deux "vecteurs de repère de base".

On peut faire beaucoup de géométrie avec les vecteurs sans utiliser de représentation avec des composantes.

Bien sûr, dès qu'on veut faire beaucoup de calculs il est bon d'avoir choisi ce qu'on appelle un repère, et alors un vecteur quelconque devient équivalent à une paire de nombres, appelés ses composantes.

Si on ne voit pas que ces composantes ne sont pas intrinsèquement liées au vecteur, mais dépendent du repère, et si on croit qu'un vecteur est nécessairement une paire de composantes, alors on sera entravé dans sa compréhension des mathématiques.

 

Exercices :

1. Additionner (4, -3) et (-2, 6).
2. Montrer que l'addition des vecteurs est associative (Suggestion : retourner au début de la cinquième pour se rappeler ce qu'est l'associativité).
3. Y a-t-il une notion naturelle de multiplication entre deux vecteurs ?

 

 

Plan général du cours

Contacter le professeur