Cours de mathématiques de 5e Expressions littérales
Video Erratum: (à 10sec: (1/4) + 6 = (1+24) divisé par 4 et non par 6)

Texte

Voici un exemple d'expression numérique :

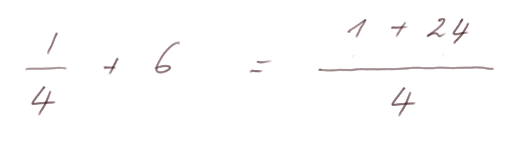
et un exemple d'expression littérale :

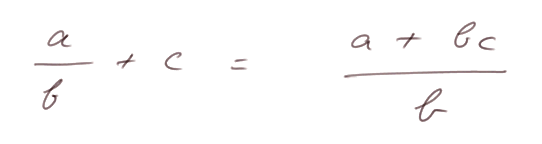
La deuxième expression est vraie quels que soient les nombres a, b et c (à la condition que b soit différent de zéro). Tandis que la première n'est qu'un exemple particulier de la deuxième, avec a = 1, b = 4 et c = 6.

La deuxième expression est vraie aussi bien si a, b et c sont des nombres entiers que des fractions. On peut le vérifier en faisant du "calcul littéral". Nous en verrons d'autres plus intéressants dans quelques instants.

On peut distinguer deux types d'expressions littérales :

1. Celles qui expriment des vérités quels que soient les nombres (en lettres) qui sont dedans. On les appelle aussi des identités.
2. Celles qui expriment une contrainte sur certains nombres. On les appelle aussi des équations.

Jusqu'à maintenant j'ai présenté des expressions numériques et littérales où il y a un signe =. En fait la lettre "a" toute seule est aussi une expression littérale. L'addition (a + b) est une expression littérale. Le nombre (a + b)/c est une expression littérale.

Mais les expressions littérales sont généralement utilisées dans des identités ou des équations.

Exemple d'équation : si aujourd'hui Pépé a 63 ans et son petit-fils Jim 3 ans, dans combien de temps Pépé aura-t-il 4 fois l'âge de Jim ? On a transformé le problème en : trouver le nombre d'années inconnu x tel que

4(x + 3) = x + 63

(Je ne mets plus le signe "multiplié par" pour ne pas créer de confusion avec le nombre inconnu x. Quand deux expressions sont accolées, ça veut dire qu'on les multiplie : 4x ou 4(x+3) ou np, etc.)

ça devient une contrainte sur l'inconnue x. On dit aussi une équation avec une inconnue.

On fait des calculs avec des chiffres et une lettre pour "résoudre le problème". On dit aussi "résoudre l'équation".

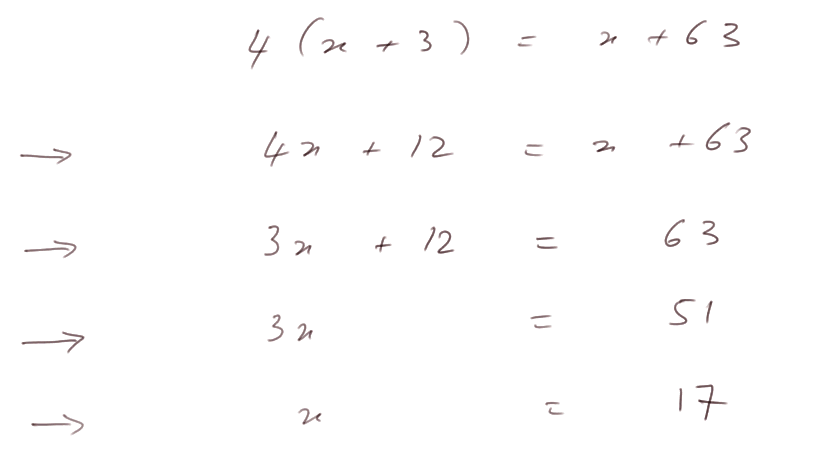
En fait, on peut faire ce calcul dans un cadre plus général qu'avec Pépé a 63 ans et Jim 3 ans. Notons "a" l'âge de Pépé, et "b" l'âge de Jim (avec b < a, et même 4b < a). Le problème reste "Quand est-ce que Pépé aura 4 fois l'âge de Jim ?". Il faut maintenant résoudre 4(x + b) = x + a

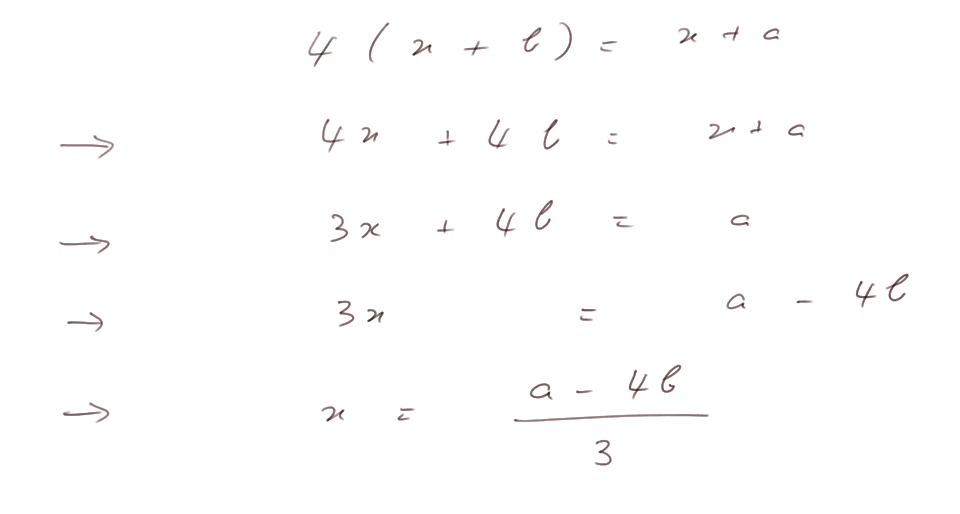
Noter que dans le premier exemple, on avait choisi a et b tels que la solution x soit un nombre entier. Mais dans le cas général le résultat peut tout à fait être une fraction qui ne se simplifie pas en nombre entier. (C'est l'une des utilités des fractions.)

 

Les expressions littérales permettent d'exprimer des vérités sans se limiter à des exemples numériques. Exemple : si j'ai un rectangle de largeur "a" et de longueur "a + 2", alors son aire est S = aa + 2a.

Le calcul avec des expressions littérales permet de résoudre des problèmes dans des cas plus généraux que de simples exemples numériques.

C'est Al Khawarizmi (c. 783, c. 850) qui dans son livre "Kitab al-Jabr" a introduit cette façon de faire des calculs avec des expressions littérales. "al-Jabr" veut dire "remplacement, complétion" et a donné le mot algèbre. Dans le calcul ci-dessus, c'est bien ce qu'on fait : on remplace, on soustrait, on ajoute, on complète, etc.

Exercices

1. Calculer la surface (= l'aire) d'un rectangle de largeur "a" et longueur "a+ 2" pour la série des onze nombres "a" suivants : 0m, 0,1m, 0,2m... 0,9m, 1m.
2. Pour quelle largeur "a" approximativement, l'aire est égale à 1m carré ?

Réponses

 

 

Plan général du cours

Contacter le professeur

 

 

Réponses

1. 
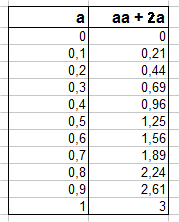
2. La surface du rectangle est 1 m² pour "a" juste un peu plus grand que 40 cm.