Cours de mathématiques de 2nde Droites et plans dans l'espace
Video

Texte

Nous avons déjà beaucoup étudié les droites dans le plan en classe de 3e. Ceux qui trouveraient cette leçon trop rapide sont invités à retourner étudier les leçons de 3e sur les droites.

Une droite est un ensemble de points de coordonnées (x, y) satisfaisant l'équation générale

ax + by + c = 0

Il existe une forme réduite (pour les droites qui ne sont pas verticales) : y = ax + b. Les coefficients ne sont pas les mêmes d'une forme à l'autre.

 

Définition avec un point et un vecteur. Maintenant que nous connaissons les vecteurs, nous pouvons décrire une droite comme un ensemble de points P = (x, y), tels que A = (x₀, y₀) appartient à la droite, et tous les vecteurs sont colinéaires (c'est-à-dire paralllèles) à un vecteur donné V = (a, b).

Cela donne la contrainte, (x - x₀ ; y - y₀) colinéaire à (a, b) :

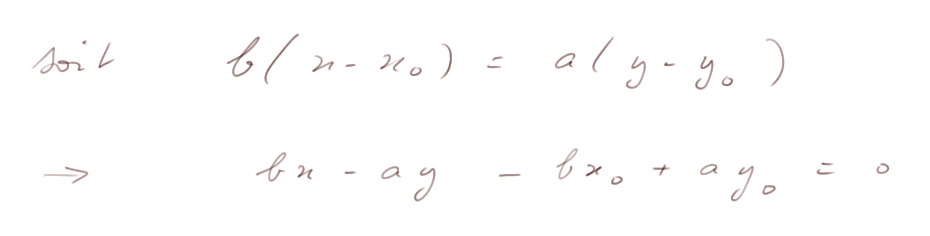
Exemple : Trouver l'équation de la droite passant par A = (-2 ; 1) et parallèle au vecteur V = (3 ; 2)

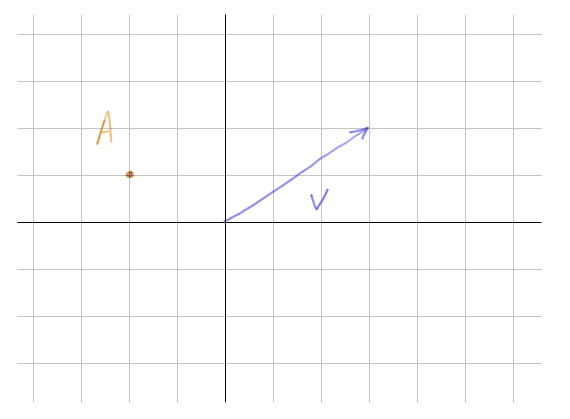
Les calculs donnent

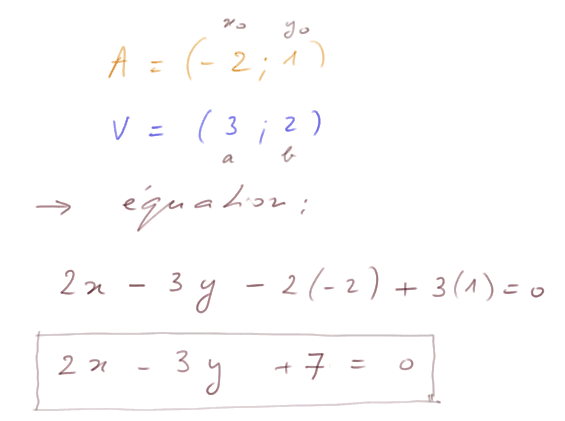
Et on vérifie que cette droite passe par A, ainsi par exemple que par (1 ; 3) ou (-5 ; -1).

 

Repère dans l'espace. Un repère dans l'espace est la généralisation de ce qu'on a vu dans le plan

 

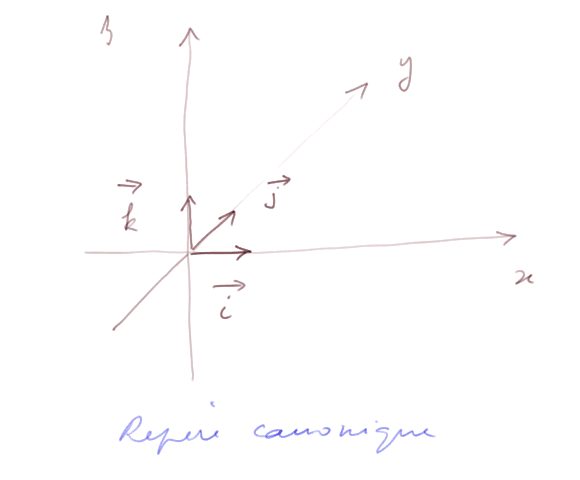
Equation d'une droite dans l'espace. C'est l'ensemble des points P = (x, y, z) passant par un point A = (x₀, y₀, z₀) et tels que les vecteurs soient colinéaires à un vecteur V = (a, b, c) donné.

Si a, b et c sont différents de zéro, cela donnent les deux contraintes

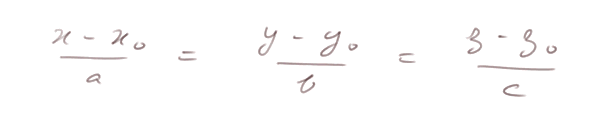
(si a, b ou c = 0, on adapte un peu ces contraintes).

 

Equation d'un plan dans l'espace. C'est l'ensemble des points P = (x, y, z) passant par un point A = (x₀, y₀, z₀) et tels que les vecteurs soient une combinaison quelconque de deux vecteurs donnés V₁ = (a, b, c) et V₂ = (d, e, f) :

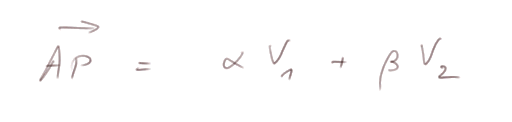
Cela donne le système suivant

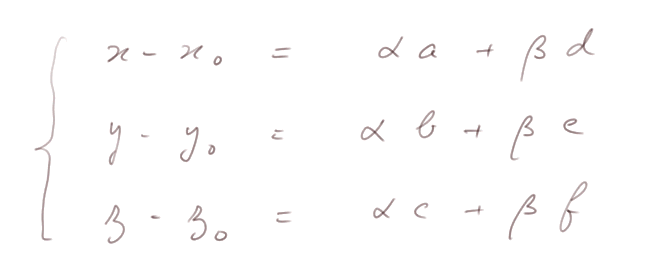
Et, après élimination des α et β, on obtient une équation linéaire de la forme

sx + ty + uz + v = 0

 

Exemple : Trouver l'équation du plan passant par A = (1 ; 1 ; 1) et parallèle aux vecteurs V₁ = (1 ; 0 ; 1) et V₂ = (0 ; 1 ; 1)

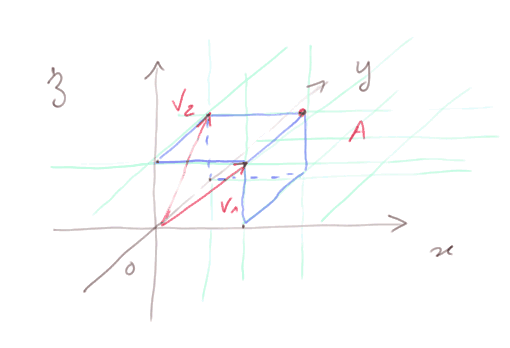
Le système ci-dessus devient

• x - 1 = α
• y - 1 = β
• z - 1 = α + β

D'où z - 1 = x - 1 + y - 1

soit x + y - z - 1 = 0.

On vérifie que ce plan passe par A, et qu'il est parallèle à V₁ = (1 ; 0 ; 1) et V₂ = (0 ; 1 ; 1). (Pour ce faire, remonter le plan de 1 verticalement, son équation devient x + y - z = 0, et ce nouveau plan contient bien les deux vecteurs.)

 

Exercices :

1. Trouver l'équation du plan passant par A = (1 ; 1 ; 2) et parallèle aux vecteurs V₁ = (1 ; 0 ; 1) et V₂ = (0 ; 1 ; 1)

 

 

Plan général du cours

Contacter le professeur