Cours de mathématiques de 2e
Statistiques : estimation de la variance d'une v.a.
Texte
Supposons qu'à la suite de n répétitions d'une expérience 
on dispose d'une série de résultats de mesure d'une variable aléatoire X :
x1, x2, x3, ... xn
On veut estimer la moyenne de X, notée E(X) ou simplement EX quand ça ne crée pas de confusion, et aussi la variance de X, qu'on a définie comme E{ (X - EX)2 }, et son écart type qui est la racine carrée de la variance.
Appelons "m" la moyenne de X, et "s" son écart type. Donc Var(X) = s2. Ce sont deux nombres inconnus. On estime m de manière naturelle avec
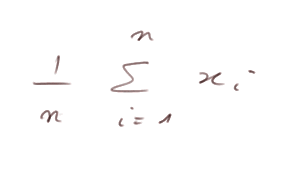
Mais comment estimer s2 ?
Dans une leçon précédente, à l'aide d'un tableur de simulation, on a montré que quand n est grand
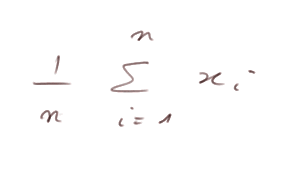
est proche de m.
On a aussi montré que
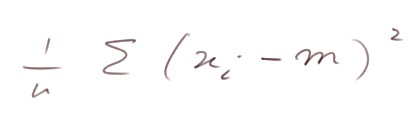
est proche de Var(X).
Mais ce n'est pas un calcul réaliste, car justement on ne connaît pas m, mais seulement son estimation avec la moyenne arthmétique des xi.
Estimation "naturelle" de s2. L'estimation naturelle de s2 consiste à remplacer m par
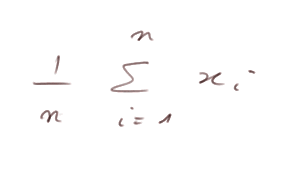
dans la formule
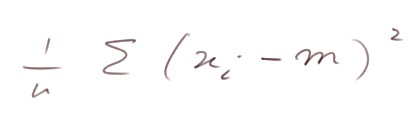
et estimer s2 par
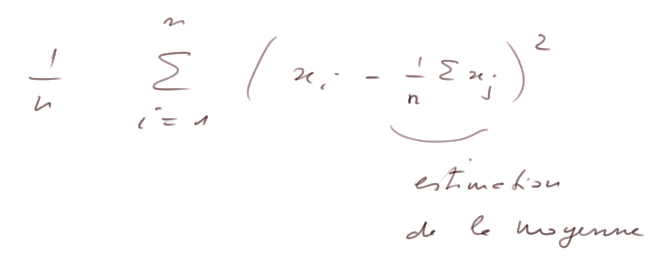
But de la leçon : montrer que cette estimation de s2 est systématiquement trop basse. (Pour être précis : sa moyenne, car c'est elle-même une variable aléatoire, est plus petite que s2.)
La raison est que (Σxi)/n n'est pas exactement m, et surtout c'est la valeur t qui minimise
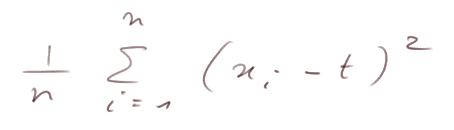
donc elle est en quelque sorte "trop bien ajustée aux xi".
Lemme : soit trois nombres a, b et c, le nombre t qui minimise (a - t)2 + (b - t)2 + (c - t)2 est la moyenne arithmétique de a, b et c :
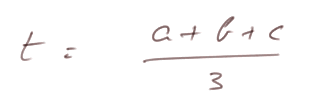
Preuve :
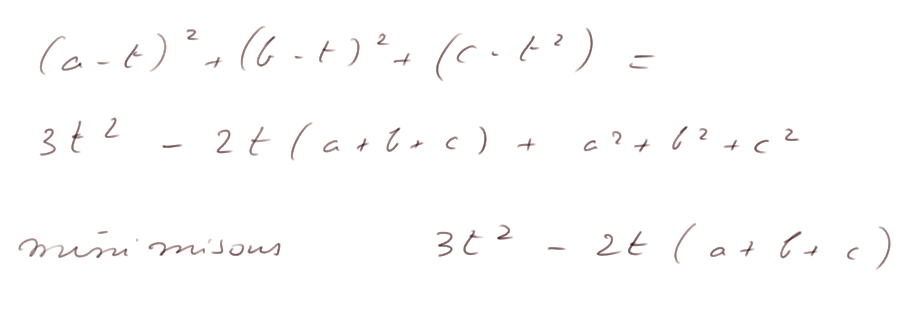
Considérons la fonction f(t) = 3t2 - 2t (a + b + c)
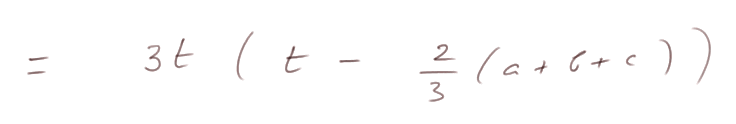
C'est une parabole tournée vers le haut, avec deux racines : 0 et (2/3)(a + b + c)
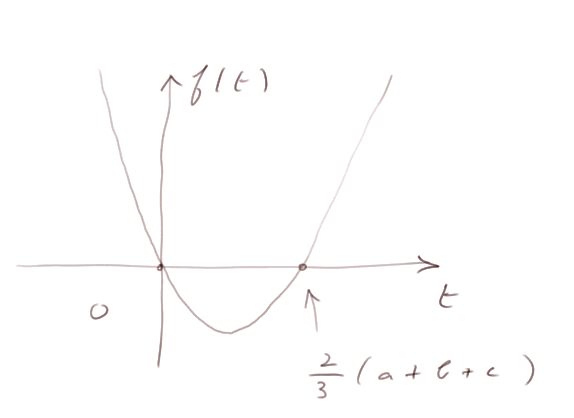
Elle a un axe de symétrie vertical à t = (a + b+ c)/3 et c'est le point t où elle est minimale.
Ce résultat est vrai non seulement pour trois nombres mais pour "n" nombres : x1, x2, x3, ... xn
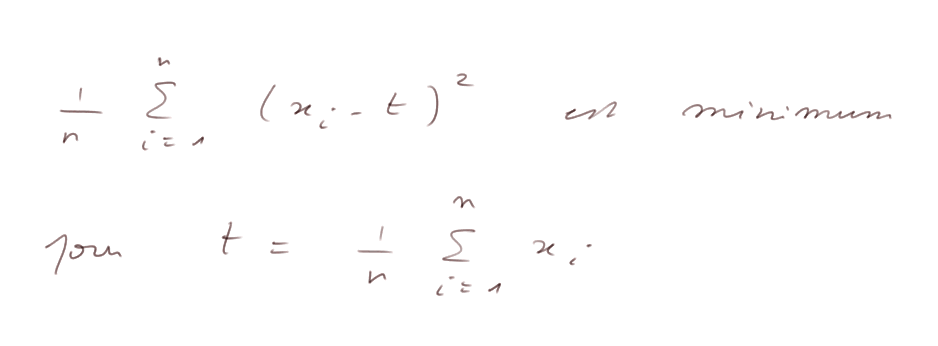
Etude avec une variable aléatoire : Soit donc une v.a. X qui peut prendre les valeurs { 100, 110, 120, 130, 140 } avec les probabilités respectives 5%, 20%, 50%, 20%, 5%.
On calcule aisément que m = 120, et s2 = 80. (Et l'écart type est s = √80 = 8,94...)
Situation réelle : Plaçons-nous dans une situation où on a quelques mesures de X, mais on ne connaît ni l'ensemble des valeurs possibles { a1, a2, a3, ... an } (quoiqu'on en connaisse forcément quelques unes grâce aux observations), ni les probabilités, ni m, ni s2.
On connaît seulement
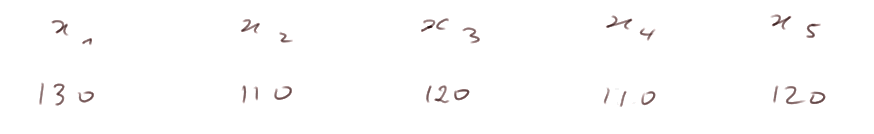
Alors une estimation de m est
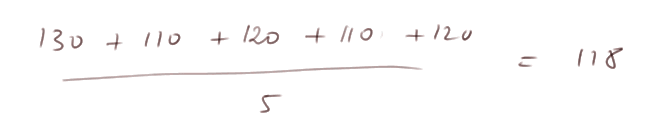
et l'estimation "naturelle" correspondante de s2 est
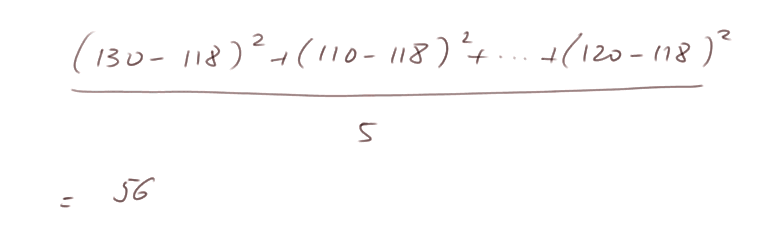
Reproduction 1000 fois de l'expérience consistant à produire 5 mesures de X. Il faut bien comprendre ce qu'on va faire : on va essayer de voir la qualité de l'estimation de m et de l'estimation de s2 ci-dessus obtenues avec seulement 5 mesures de X.
Appelons 
l'expérience consistant à répéter 
cinq fois.
On va répéter 1000 fois, et chaque fois on va calculer l'estimation de m et celle de s2 et voir comment elles se comportent sur 1000 tirages.
Lors de la répétition de 1000 fois, à l'aide du tableur estimation_variance.xls, les 1000 calculs des deux estimations ont eu les moyennes suivantes :
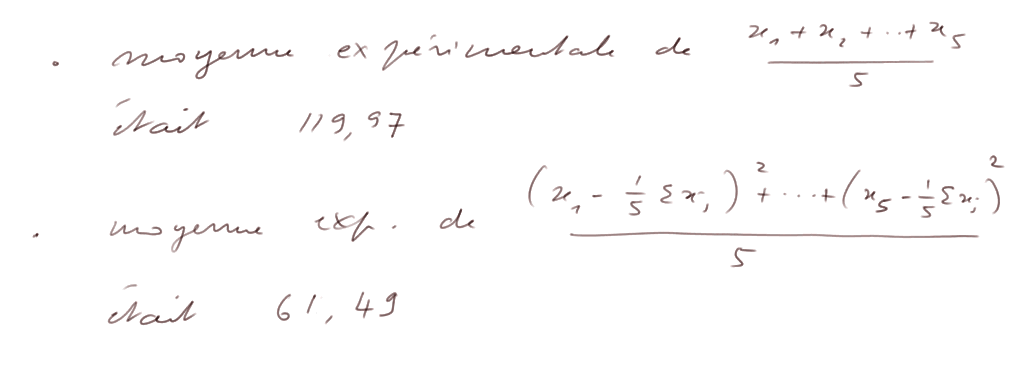
Voici le tableur qui a donné ça :
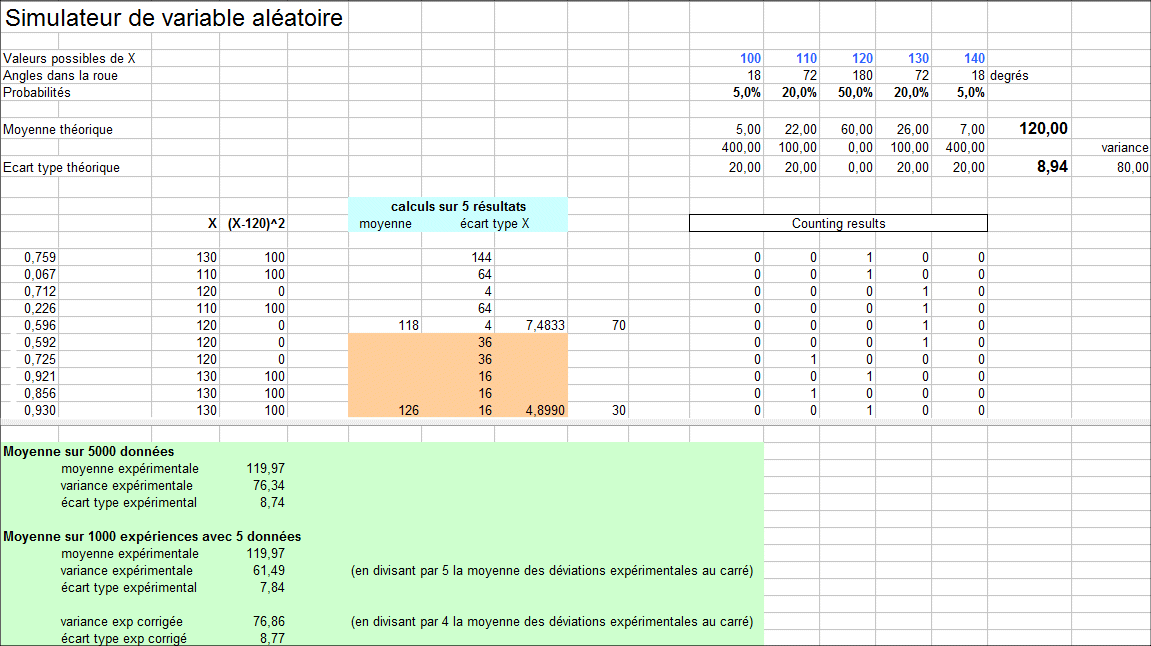
Répétition de "1000 " quelques fois. On a même répété "1000 " quelques fois (c'est équivalent à répéter beaucoup plus que 1000 fois) et on a observé ceci :
On voit donc que la moyenne se comporte bien, mais pas la variance estimée, qui est trop faible par un facteur 64/80 = 4/5.
La raison est que quand on a 5 nombres x1, x2, ... x5
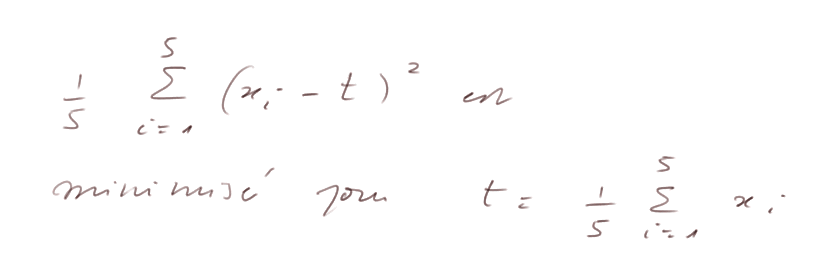
Donc la variance est mal estimée. Elle le serait bien si on pouvait calculer
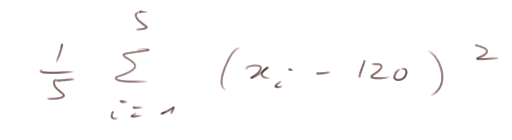
Insistons sur l'explication : considérons x1, x2, ... x5 comme des variables aléatoires dans
Epilogue : En fait on montrera plus tard que
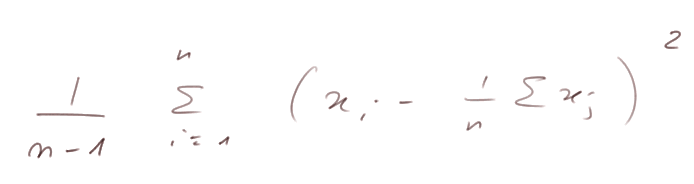
(c'est-à-dire où on divise par "n - 1" et non pas "n") est une bonne estimation de s2 (= VarX).
Et on vérifie que 64 x 5 / 4 = 80 = variance de X.
Il y a des chances que votre calculette scientifique calcule la variance d'une série de nombres en divisant les déviations au carré par rapport à leur moyenne, par "n - 1".
Noter enfin que ce raffinement qui consiste à diviser par "n - 1" au lieu de "n" n'a d'importance que quand n est petit, car quand n est grand diviser par "n " ou "n - 1" ne fait pas de différence significative.
Par ailleurs, il faudra se pencher plus tard sur "qu'est-ce qu'on veut dire par une bonne estimation ?" Ici on est parti du principe de bon sens qu'il fallait au moins qu'elle ait pour moyenne le nombre qu'elle estime. Mais on verra que ce raisonnement de bon sens et quelques autres tout aussi sensés conduisent à d'étonnants paradoxes.
Exercices :
- A l'aide du tableur estimation_variance.xls, modifier les valeurs possibles de X, ainsi que leurs probabilités, et vérifier que les résultats de la leçon (principalement : pour estimer une variance, il faut diviser la somme des déviations estimées au carré par "n - 1" et non pas "n") restent vrais.
Les écrans de la vidéo
écran 1
écran 2
écran 3
écran 4
écran 5
écran 6
écran 7
écran 8
écran 9
écran 10
écran 11
écran 12
écran 13
écran 14
écran 15
écran 16
écran 17
Plan général du cours
Contacter le professeur