Cours de mathématiques de 2nde Nombres premiers (3) : quelques propriétés
Video

Texte

Après les deux dernières leçons exigeantes sur les nombres premiers, dans cette leçon nous nous promènerons au milieu d'autres propriétés de ces nombres sans rien démontrer.

On se rappelle tout d'abord le "théorème fondamental de l'arithmétique" : tout nombre entier a une décomposition unique en facteurs premiers (à l'ordre près).

Sommes d'inverses :

• On a vu dans un cours passé que la somme des inverses de tous les nombres entiers tend vers plus l'infini. On note ceci
  
  
  
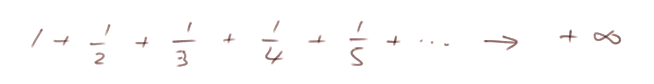
  (cette notation ne veut rien dire d'autre que "en allant suffisamment loin dans la somme, on peut la rendre aussi grande qu'on veut")
  
  
• La somme des inverses des puissances de 2, tend vers 2. On note ceci
  
  
  
  
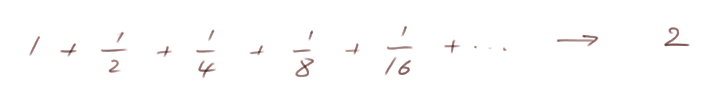
• Eh bien, la somme des inverses des nombres premiers tend vers plus l'infini.
  
  

Tests de primalité : Un problème important en mathématiques, étant donné un nombre n, est de déterminer s'il est premier ou pas. (Ça sert en particulier en cryptographie, mais pas seulement.) Le test le plus élémentaire est d'essayer de diviser n par tous les nombres entiers jusqu'à sa racine carrée. Mais c'est un test rapidement très lourd et pas très efficace. Il y a mieux.

Il existe des algorithmes modernes plus efficaces.

• Certains sont "déterministes" : ils répondent de manière indiscutable "n est premier" ou bien "n n'est pas premier".
• D'autres sont "probabilistes" : ils répondent soit "n n'est sûrement pas premier" ou bien "n est probablement premier".

Curieusement, dans la pratique, une telle réponse ("n est probablement premier") est parfois suffisante.

Regardons comment on construit un test de primalité probabiliste en utilisant le Petit théorème de Fermat. Soit un nombre n donné. Nous voulons tester si n est premier ou pas.

On sait, en particulier, que pour tout "a" tel que 1 < a < n (et aussi pour les a plus grands que n mais non multiples de n), si le reste de la division de a^n-1 par n est différent de 1 alors n n'est pas premier.

Mais l'inverse n'est pas vrai : n peut ne pas être premier et néanmoins pour certains "a", la division de a^n-1 par n peut donner 1. (Ce qui veut dire que a^n-1 et n sont premiers entre eux.) Pour certains nombres n non premiers c'est même vrai pour tous les a tels que 1 < a < n. Ces nombres n sont appelés "nombres de Carmichael".

Cependant, les nombres de Carmichael sont rares et souvent on procède de la manière suivante pour tester un nombre n : on essaie pour quelques a tels que 1 < a < n, et si chaque fois on a verifié que a^n-1 et n étaient premiers entre eux, alors on déclare que "n est probablement premier".

 

 

Formules pour calculer les nombres premiers : il n'existe pas de formule pratique permettant de calculer tous les nombres premiers dans l'ordre. Néanmoins Euler a observé que n² - n + 41 donnait exclusivement des nombres premiers pour n compris entre 1 et 40 (inclus).

 

Arithmétique modulo n : il existe une façon amusante et, au départ, simple de faire de l'arithmétique dans un ensemble fini de nombres entiers. On prend l'ensemble des nombres entiers de 0 jusqu'à n-1 inclus :

Soient deux nombres a et b dans cet ensemble, alors on définit les opérations habituelles d'addition, de soustraction et de multiplication en faisant le calcul normal et puis en ne prenant que le reste dans la division par n.

Exemple : arithmétique modulo 6

• 3 + 5 = 2 (mod 6), car 8 divisé par 6 donne comme reste 2
• 3 - 5 = 4 (mod 6), car on peut rajouter 6 à 3 sans rien changer, et 9 - 5 = 4
• 3 x 5 = 3 (mod 6)

mais la division ne marche pas dans l'arithmétique modulo 6. Par exemple il n'y a aucun nombre m tel que 3 x m = 2 (mod 6), car le résultat de 3 x m est toujours soit 0 soit 3.

Mais si n est premier, alors l'arithmétique modulo n a aussi une division qui marche bien (et réciproquement). Exemple : prenons n = 7

3 x m = 2 (mod 7) a une solution unique, m = 3

 

Exercices :

1. Etablir la table d'addition et la table de multiplication en arithmétique modulo 7.
2. Vérifier que a x b = 0 (mod 7) si et seulement si a ou b =0.
3. Vérifier que tout nombre non nul a un inverse, et qu'il est unique.
   
   

 

Plan général du cours

Contacter le professeur