Cours de mathématiques de 2ndeOrthogonalité dans le plan et dans l'espace |
|
Video |
Texte
- être perpendiculaire à...
- être orthogonal à...
- faire un angle de 90° (= π / 2) avec...
Ainsi dans le plan deux vecteurs sont orthogonaux s'ils font entre eux un angle orienté de π/2 ou -π/2
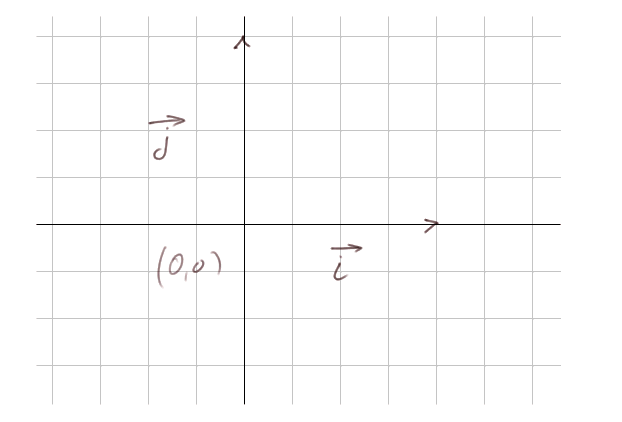
Orthogonalité vue dans le repère habituel. Considérons maintenant le plan avec le repère habituel ![]() . On a pris un quadrillage d'un quart d'unité pour bien voir ce qui se passe autour de l'origine. Les vecteurs
. On a pris un quadrillage d'un quart d'unité pour bien voir ce qui se passe autour de l'origine. Les vecteurs ![]() et
et ![]() sont chacun de longueur 1 et orthogonaux entre eux.
sont chacun de longueur 1 et orthogonaux entre eux.
Caractérisation algébrique de l'orthogonalité. Soit deux vecteurs V1 et V2 sur le cercle trigonométrique de coordonnées
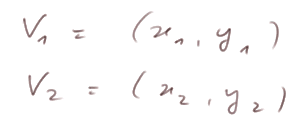
alors on a la relation très importante suivante : V1 est orthogonal à V2 si est seulement si x1x2 + y1y2 = 0
Preuve : Commençons par l'implication dans le sens "gauche vers droite" (qui correspond au "seulement si" de l'expression "si et seulement si") :
Si V1 et V2 sont orthogonaux, appelons θ l'angle entre l'axe des x et V1.
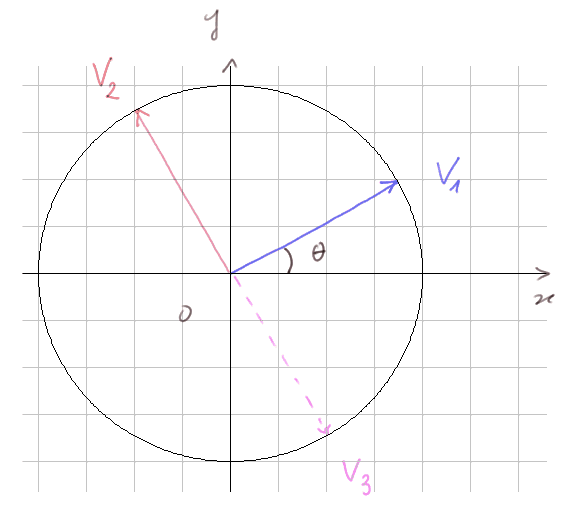
Alors on a
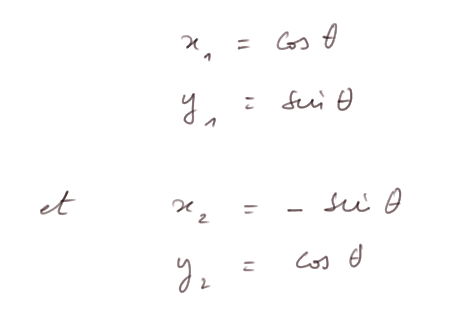
donc x1x2 + y1y2 = -cosθsinθ + sinθcosθ = 0
Réciproquement : si x1x2 + y1y2 = 0 alors x1x2 = -y1y2. Ça donne
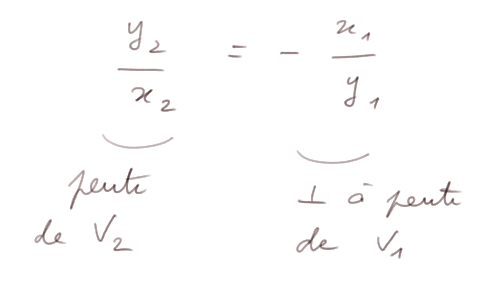
En effet regardons le cercle trigonométrique avec V1, et V2 que je n'ai pas représenté.
D'une part y2/x2 est la pente d'une droite ayant V2 pour vecteur générateur.
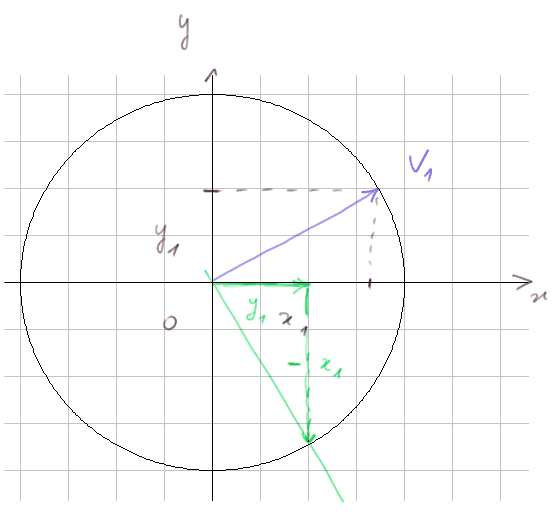
D'autre part -x1/y1 est la pente d'une droite perpendiculaire à V1. Puisque c'est une droite sur laquelle quand on se déplace de y1 sur l'axe des x (dessin en vert ci-dessus), on se déplace de -x1 sur l'axe des y.
Donc V2 est orthogonal à V1.
Le fait que V1 et V2 soient sur le cercle trigonométrique n'est pas important car on peut multiplier l'un ou l'autre par un scalaire sans changer l'identité x1x2 + y1y2 = 0.
Donc, d'une manière générale :
Dans le plan, deux vecteurs V1 et V2, dont les coordonnées dans le repère ![]() sont (x1, y1) et (x2, y2), sont orthogonaux si et seulement si x1x2 + y1y2 = 0
sont (x1, y1) et (x2, y2), sont orthogonaux si et seulement si x1x2 + y1y2 = 0
C'est une relation importante que nous étudierons plus à fond, étendrons et utiliserons pendant des années.
Dans l'espace. Ce résultat est aussi vrai dans l'espace à 3 dimensions :
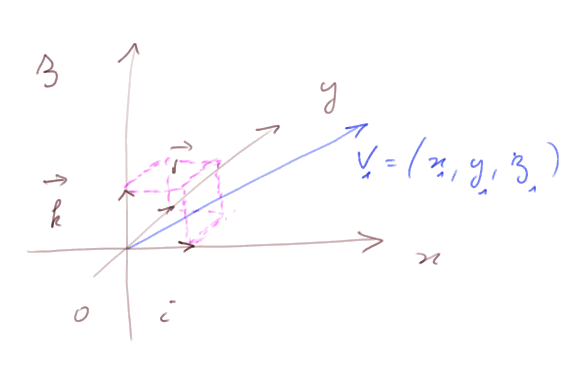
Deux vecteurs V1 et V2 de coordonnées (x1, y1, z1) et (x2, y2, z2) sont orthogonaux si et seulement si x1x2 + y1y2+ z1z2 = 0
Preuve :
Les points M dans l'espace tels que le vecteur OM soit perpendiculaire à V1 sont dans un plan.
Dans ce plan se trouvent par exemple les points P = (-y1, x1, 0) et Q = (0, -z1, y1). On l'établit avec un peu de géométrie dans l'espace, qui est laissée au lecteur.
Tous les autres points M du plan perpendiculaire à V1 sont tels que le vecteur OM est une combinaison linéaire des vecteurs OP et OQ
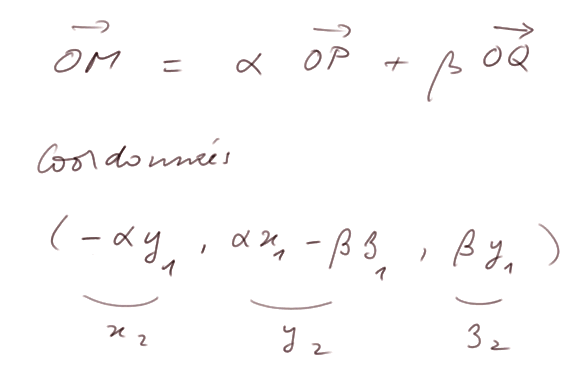
Alors on vérifie que x1x2 + y1y2+ z1z2 = 0.
Réciproquement : si x1x2 + y1y2+ z1z2 = 0, écrivons le vecteur OM comme une combinaison linéaire des vecteurs OP, OQ et V1 (c'est possible, car ils forment un repère dans l'espace).
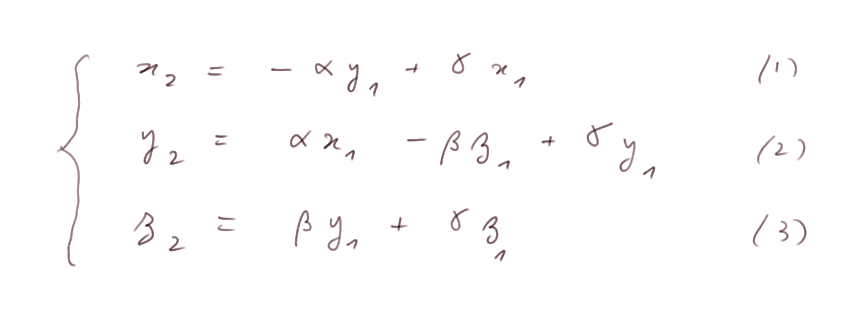
Multiplions l'équation (1) par x1, l'équation (2) par y1 et l'équation (3) par z1 et additionnons-les. On doit obtenir 0 par hypothèse.
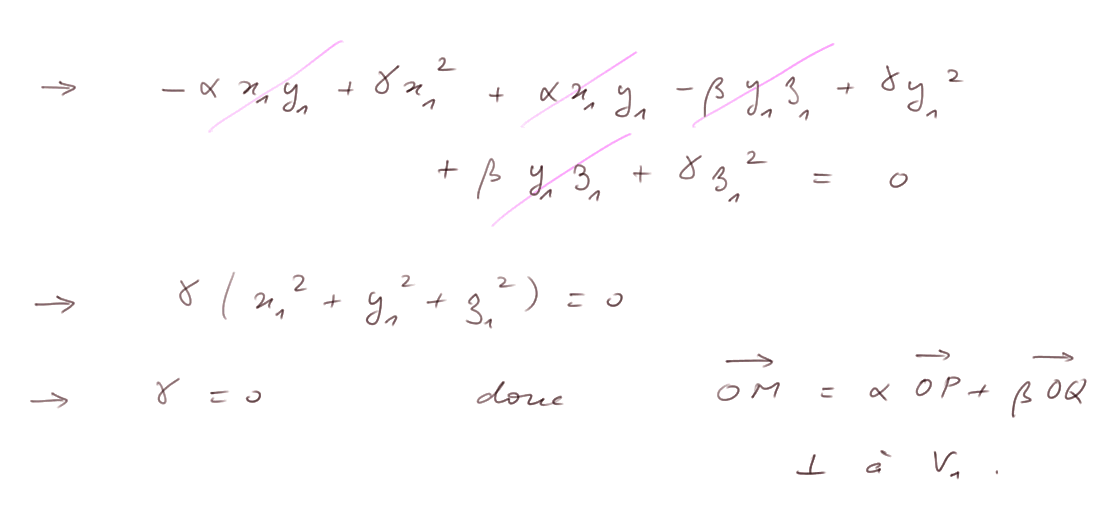
Application : soit un plan P (ici la notation n'est plus pour un point mais pour un plan) d'équation
ax + by + cz + d = 0
et un point M0 dans le plan. Alors ax0 + by0 + cz0 = -d.
On en déduit que pour tous les points M du plan P on a l'identité
![]()
C'est-à-dire que le vecteur M0M est orthogonal à un vecteur de coordonnées (a, b, c).
Interprétation géométrique. On voit donc que l'équation d'un plan, ax + by + cz + d = 0, a une interprétation géométrique très simple :
le plan P d'équation ax + by + cz + d = 0 est formé d'un point quelconque M0 et de tous les points M tels que le vecteur M0M est orthogonal au vecteur de coordonnées (a, b, c)
Exemple numérique. Ecrire l'équation du plan P passant par M0 = (0 ; 0 ; 1) et perpendiculaire au vecteur V = (2 ; 3 ; 4).
Solution : on veut que 2x + 3y + 4z + d = 0, donc d doit être égal à -4. Et le plan P est formé de l'ensemble des points (x, y, z) tels que
2x + 3y + 4z - 4 = 0
Exercices :
- Trouver les équations du plan P1 passant par (0 ; 0 ; 1) et perpendiculaire à (1 ; 2 ; 3) et du plan P2 passant par (0 ; 1 ; 0) et perpendiculaire à (2 ; 2 ; 1).
- Montrer qu'ils ne sont pas parallèles.
- Trouver un vecteur générateur de leur droite d'intersection.