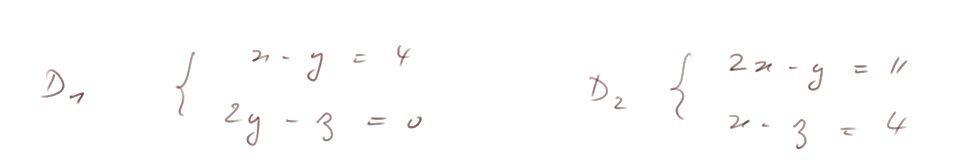Cours de mathématiques de 2ndeParallélisme dans le plan et dans l'espace |
|
Video |
Texte
- de façon purement géométrique dans une figure
- comme l'ensemble des points P, qui contient un point donné A, et tel que pour tout point P
est colinéaire à un vecteur donné 
- avec une équation algébrique : ensemble des points (x, y) tels que ax + by + c = 0 (et si b ≠ 0 il y a aussi l'équation réduite y = ax + b, ce ne sont pas les mêmes a et b)
Parallélisme dans le plan. Deux droites, dans le plan, sont parallèles si et seulement si
- elles ne se coupent pas
- (ou de manière équivalente) elles ont, dans le cas où elles ne sont pas verticales, le même coefficient directeur dans l'équation réduite y = ax + b (et les ordonnées à l'origine sont distinctes)
- (ou de manière équivalente) quand on considère les équations générales a1x + b1y + c1 = 0 et a2x + b2y + c2 = 0, alors a1b2 = a2b1
(noter que la condition a1b2 = a2b1 est une façon d'exprimer a1 / b1 = a2 / b2, qui tient compte du cas possible b1 = b2 = 0, c'est-à-dire des droites verticales)
Dans tous les cas, dans le plan, deux droites sont parallèles, si et seulement si leurs vecteurs générateurs sont colinéaires.
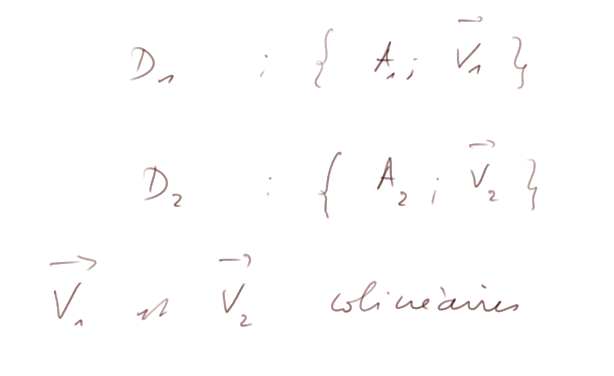
Une remarque sur les notations. Il ne faut pas prêter trop d'importance aux notations. Elles doivent avant tout pouvoir être lues ou interprétées en bon français.
est la notation que j'utilise pour simplement dire : "la droite qui passe par A et dont tous les points P sont tels que est colinéaire au vecteur ".
Parfois, comme en algèbre, les notations se prêtent à des manipulations mécaniques simples, qui tendent à faire oublier que ce ne sont que des notations. Ce sera aussi souvent le cas en calcul intégral, et c'est d'ailleurs un des problèmes des notations inventées par Leibniz en calcul intégral et différentiel, qui peuvent entraîner à faire n'importe quoi, quand on perd de vue ce qu'elles veulent dire. On verra ça en Terminale.
Parfois, les notations sont seulement là pour exprimer de manière abrégée des phrases explicites.
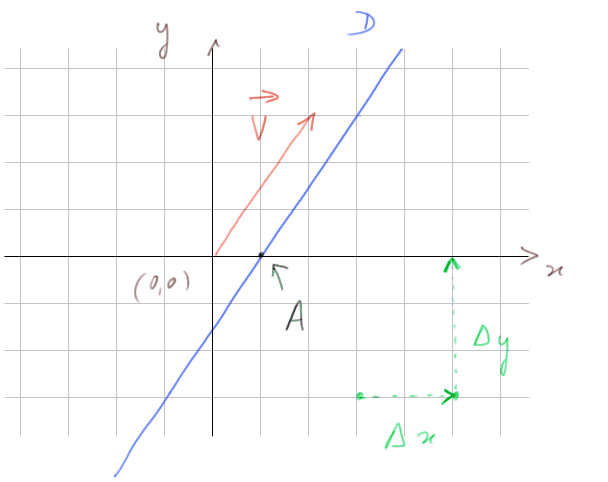
Exemple d'équation de droite à partir de A et : Soit D la droite définie par
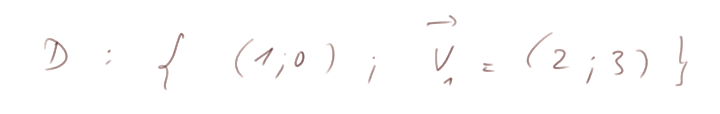
Comme elle n'est clairement pas verticale, elle a donc une équation réduite y = ax + b. On peut déterminer a et b à partir de A et .
Etant donné que A est sur la droite D, on a 0 = a + b.
Et comme D est parallèle à , on sait que chaque fois qu'on se déplace sur D avec un Δx = 2 en abscisse, alors en ordonnée on se déplace d'un Δy = 3. Donc le coefficient directeur est forcément a = 3/2 (ou 6/4, etc. c'est pareil). L'équation de la droite est donc
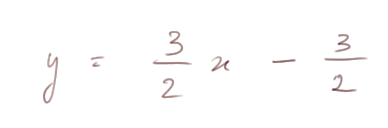
Voyons cela avec un dessin dans le repère habituel :
Dans l'espace. La définition "deux droites sont parallèles si elles ne se coupent pas" ne marche plus ! Il y a plein de droites qui ne se coupent pas mais qui ne sont pas parallèles, car il y a "suffisamment de place" dans l'espace à trois dimensions.
Mais la définition avec les points et vecteurs directeurs marche toujours : deux droites sont parallèles si leurs vecteurs directeurs (dits aussi "générateurs") sont colinéaires.
Droite dans l'espace, définie par A et . Soit la droite D définie par
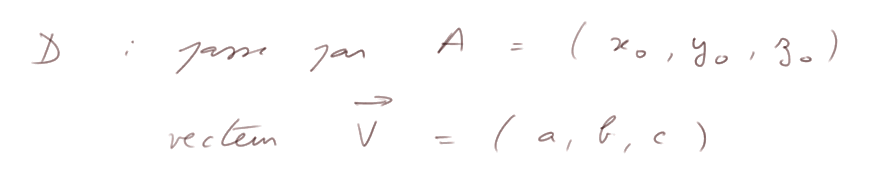
Alors ses équations (au pluriel) sont par exemple :
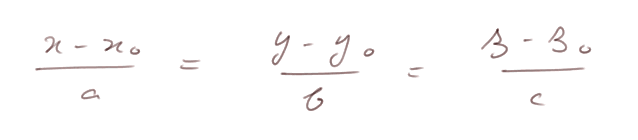
(Ici je suis dans le cas où le vecteur générateur a ses trois composantes non nulles. Si est parallèle à un des plans Oxy, Oxz, ou Oyz, on adapte un peu les équations.)
Noter qu'il faut deux équations de plans pour définir une droite dans l'espace. La droite est l'ensemble des points qui sont à la fois sur chaque plan.
Exemple. Soit
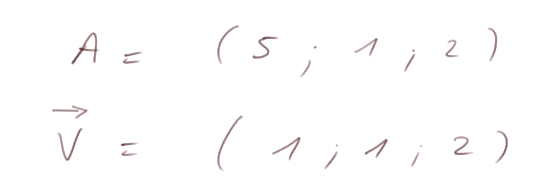
Alors un jeu d'équation pour la droite est par exemple :
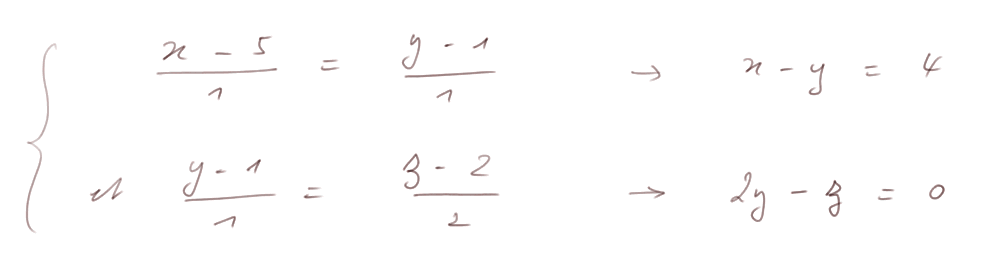
Ce n'est pas le seul jeu d'équations qui définisse la droite. Tout simplement car il y a plusieurs paires de plans dans l'espace qui définissent la même droite (en fait toutes les paires de deux plans distincts qui justement contiennent cette droite...). Par exemple, la première équation, plus celle obtenue en additionnant la première et la deuxième, forment aussi un jeu qui définit la même droite.
Droite parallèle à une droite donnée. Une autre droite, D2, sera parallèle à D1, définie par A et , si et seulement si est aussi un des vecteurs générateurs possibles pour D2.
Question : dans l'espace, comment reconnaître à partir de leurs jeux d'équations si deux droites sont parallèles ou pas ?
Réponse 1 : trouver si elles appartiennent à un même plan, et,si oui, dans ce plan voir si elles sont parallèles.
Mais cette réponse la plupart du temps ne nous avance pas beaucoup. Voici une réponse plus utile :
Réponse 2 : Dans la pratique, pour déterminer si D1 et D2 sont parallèles,
- trouver 2 points A1 et B1 sur D1, et 2 points A2 et B2 sur D2, et
- regarder si
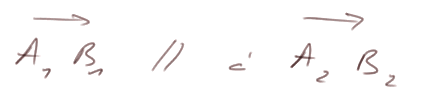
Exemple. Soient D1 et D2 ayant les jeux d'équations suivants :
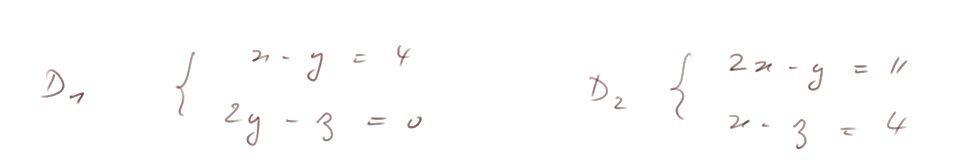
Alors, en farfouillant un peu, on trouve les points
On a
Ces vecteurs ne sont pas colinéaires, c'est-à-dire qu'il n'y en a pas un qui soit un multiple de l'autre, avec un coefficient réel non nul quelconque. Donc les deux droites ne sont pas parallèles.
On peut même vérifier qu'elles ne se coupent pas (c'est l'exercice de fin de leçon).
Plans dans l'espace.
- C'est un peu "comme les droites dans le plan".
- C'est plutôt plus simple que les droites dans l'espace.
- Deux plans sont parallèles si et seulement si ils ne se coupent pas (auquel cas ils auraient pour intersection toute une droite, voire tout eux-mêmes)
Avec des équations de plan. Soient les deux plans P1 et P2 définis par les équations suivantes
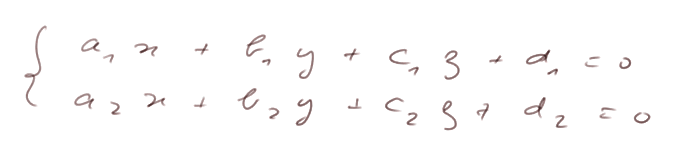
alors P1 et P2 sont parallèles si et seulement si il existe une constante λ telle que
Conclusion. Il est important de bien maîtriser toutes les notions de cette leçon. Elles nous préparent à deux notions importantes
- l'orthogonalité (sujet de la leçon suivante)
- le produit scalaire de deux vecteurs (sujet d'une leçon de 1ère)
A l'inverse, quand nous serons familiers avec l'orthogonalité et le produit scalaire, les parallélismes dans le plan et dans l'espace deviendront encore plus simples à comprendre.
Exercices :
- Montrer que les deux droites dans l'espace définies par les équations ci-dessous ne se coupent pas