Cours de mathématiques de 2nde Moyenne d'une variable aléatoire numérique
Video

Texte

Considérons une expérience aléatoire et l'ensemble Ω des états possibles du résultat de . C'est-à-dire "faire ", c'est produire un "état des choses" ω, et

ω ∈ Ω

 

Considérons une variable aléatoire X, c'est-à-dire une mesure de quelque chose sur ω, et supposons que cette variable aléatoire soit numérique (ce n'est pas une couleur, une opinion, un sexe, un type de caillou, etc., c'est un nombre) :

Si on répète trois fois, on produit ω₁, ω₂, ω₃. Et on notera les trois résultats pris par X : x₁, x₂, x₃.

 

Lancer d'un dé. Soit le lancer d'un dé.

• Ω reste un ensemble un peu abstrait "d'états de la réalité" après avoir effectué l'expérience .

• X = nombre apparaissant sur le dessus du dé. Donc X est une fonction de Ω vers { 1, 2, 3, 4, 5, 6 }
• L'ensemble { 1, 2, 3, 4, 5, 6 } s'appelle l'ensemble des valeurs possibles de X.
  
  

Pourquoi ce modèle un peu compliqué ? Pourquoi ne pas simplement modéliser cette situation avec Ω, l'univers de résultats de, = { 1, 2, 3, 4, 5, 6 } ?

Réponse : On pourrait tout à fait procéder ainsi. Mais ça compliquerait les choses ultérieurement. Par exemple, dans une expérience où on serait amené à étudier deux variables aléatoires conjointement, X et Y, il faudrait considérer un nouvel univers Ω correspondant au "produit" des ensembles des valeurs possibles de X et des valeurs possibles de Y.

Tandis qu'avec notre modèle où Ω est l'ensemble abstrait des "états de la réalité" après , le fait d'étudier une ou plusieurs v.a. (= variables aléatoires) ne change rien. On a simplement une ou plusieurs fonctions de Ω vers des ensembles de valeurs possibles :

• X : Ω -> ensemble des valeurs possibles de X
• Y : Ω -> ensemble des valeurs possibles de Y

 

Donc ici est le lancer d'un dé, et X est le nombre apparaissant sur le dessus du dé. X : Ω -> { 1, 2, 3, 4, 5, 6 }

Cet ensemble des valeurs possibles de la variable numérique X est souvent noté { a₁, a₂, a₃, ... a_n }. Il s'agit du cas où X peut prendre un nombre fini de valeurs numériques. Il existe d'autres cas qu'on étudiera plus tard.

 

Résultats expérimentaux de X. Si on effectue l'expérience un grand nombre de fois N (imaginer N = 10 000 par exemple), alors les résultats successifs de X seront notés

x₁, x₂, x₃, ... ... ... ... ... ... x_N

où chaque x_i ∈ { 1, 2, 3, 4, 5, 6 }.

 

Probabilités. Supposons que

• Probabilité { X = a₁ } = p₁
• Probabilité { X = a₂ } = p₂
• ...
• Pr { X = a_n } = p_n

avec chaque p_i > 0 et p₁ + p₂ + p₃ + ... + p_n = 1.

Par exemple, dans le cas d'un dé, on a

• Pr { X = 1 } = 1/6 = 16,66...%
• Pr { X = 2 } = 1/6
• ...
• Pr { X = 6 } = 1/6

 

Moyenne d'une variable aléatoire numérique. Dans le cas du dé, on appelle "moyenne de X" le nombre noté EX ci-dessous

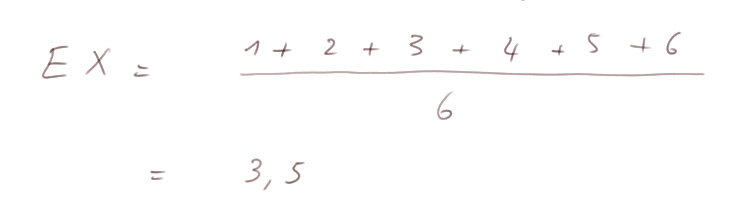
Observons tout de suite que la moyenne d'une v.a. n'est pas nécessairement une de ses valeurs possibles.

Dans le cas général, on définit EX par

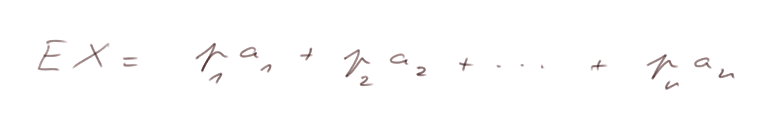
Cette formule s'appelle aussi, en mathématiques, la "moyenne pondérée" des nombres a₁, a₂, a₃ jusqu'à a_n.

Les p_i sont les "poids" dans la moyenne pondérée.

Un autre nom de "la moyenne de X" est "l'espérance mathématique de X".

 

Exemple de moyenne pondérée. Soit les deux nombres 30 et 57, alors

(1 x 30 + 2 x 57) / 3

est la moyenne pondérée de 30 et 57 avec le poids 1 sur 30 et le poids 2 sur 57. Le résultat est 48.

Cette "moyenne pondérée" est plus près de 57 que de 30 (elle est différente de la moyenne arithmétique), car 57 "a plus de poids" que 30. Elle aux deux tiers du segment [ 30 ; 57 ] vers 57.

 

Pourquoi la moyenne d'une v.a. est un nombre intéressant et naturel ?

Réponse : Parce que dans une très grande série de réalisations de , la moyenne arithmétique suivante

est presque toujours proche de EX.

 

En d'autres termes, dans une série de répétitions de , la moyenne arithmétique du grand nombre de résultats expérimentaux de X se rapproche de la moyenne pondérée (avec les probabilités) des résultats possibles de X.

 

Preuve heuristique : Au numérateur de la formule

on a a₁ qui va apparaître environ p₁ x N fois (c'est-à-dire la "fréquence théorique" de a₁ multipliée par le nombre de tirages).

De même on a a₂ qui va apparaître environ p₂ x N fois. Etc.

Donc

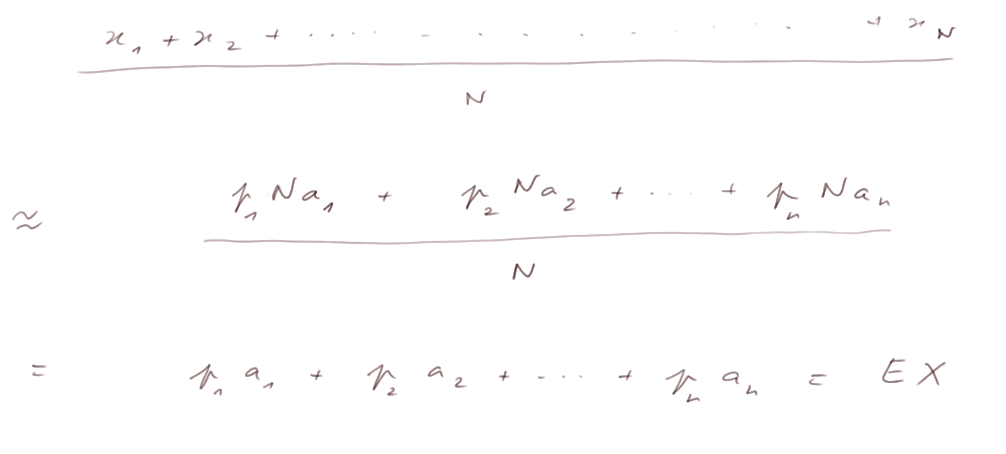
Là encore, il n'y a aucune magie. C'est juste un résultat de dénombrement : dans toutes les suites possibles ( x₁, x₂, x₃, ... ... ... ... ... ... x_N ) (et il y en a un très grand nombre), pour la plupart d'entre elles on a

On démontrera ce résultat dans une classe ultérieure. Il s'appelle : la loi des grands nombres.

Mais il est important d'en avoir une compréhension pratique, et de construire son intuition concernant ce genre de phénomène.

 

Tableur de simulations pour étudier dans la pratique la loi des grands nombres. Le tableur suivant simulation_roue_fortune.xls simule une série de 5000 répétitions de l'expérience , consistant à lancer la "roue de la fortune" suivante

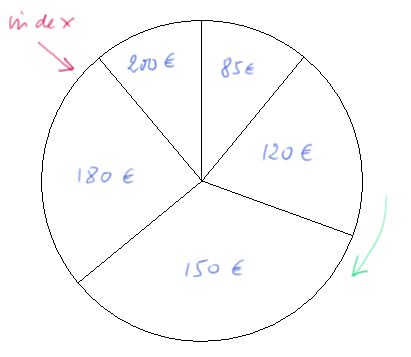
L'index rouge est fixe par rapport au support de la roue. On lance la roue. On attend qu'elle s'arrête. Et on regarde quelle somme montre l'index.

C'est une expérience aléatoire produisant une v.a. X pouvant prendre les valeurs { 85€, 120€, 150€, 180€, 200€ }. Les probabilités sont naturellement proportionnelles aux angles dans lesquels se trouve chaque somme.

On utilisera beaucoup cette "roue" construite avec un tableur pour étudier une v.a. (= valeur aléatoire) dans la pratique.

Ici on calcule que la moyenne de X est 150€ (voir les angles et donc les probabilités dans le tableur ; on peut d'ailleurs les changer si on veut, ainsi que les valeurs possibles, à la condition que la somme des angles fasse toujours 360° !).

Et le tableur permet de voir que la moyenne arithmétique expérimentale de 5000 lancers tombe toujours près de 150.

On verra quelle somme il est logique de vouloir payer pour jouer à ce jeu, si le gain est ensuite la somme montrée par l'index.

 

Exercice : soit un modèle complet ( , Ω, P ), c'est-à-dire, une expérience, son univers d'états possibles, et une fonction de probabilité P attachée à et Ω.

Et soit une v.a. X : Ω -> { 80, 90, 100, 110, 120 }.

Supposons que les probabilités respectives de chaque valeur possible de X soient

20%, 30%, 20%, 15% et 15%.

Calculer la moyenne de X.

Réponse :

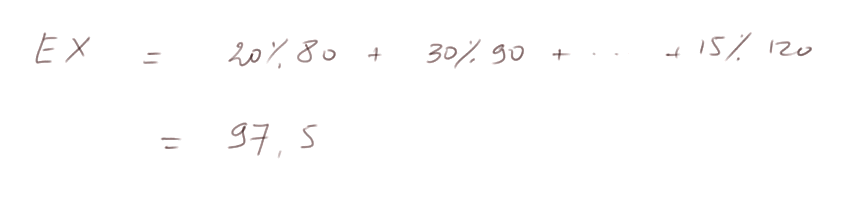
Exercices :

1. Utiliser le tableur simulation_roue_fortune.xls pour vérifier la solution de l'exercice ci-dessus.
2. Quels sont les angles que vous avez dû rentrer pour créer les probabilités 20%, 30%, 20%, 15% et 15% ?
3. Lancer le tableur 10 fois (touche F9 chaque fois) et faire la liste des 10 résultats expérimentaux de la moyenne de 5000 lancers.
4. Sont-ils toujours proches de 97,5 ?
   
   

 

 

Plan général du cours

Contacter le professeur