Cours de mathématiques de 2nde Propriétés avancées des triangles
Video

Texte

Nous avons vu en classe de 4e la "formule des sinus" dans un triangle. Soit un triangle quelconque

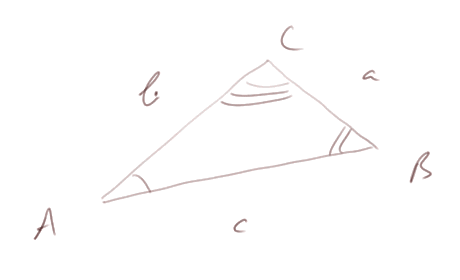
alors on a

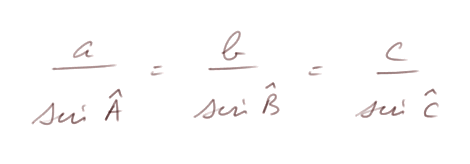
Nous allons en donner une nouvelle démonstration et montrer que ces trois ratios sont égaux à 2R, où R est le rayon du cercle circonscrit au triangle.

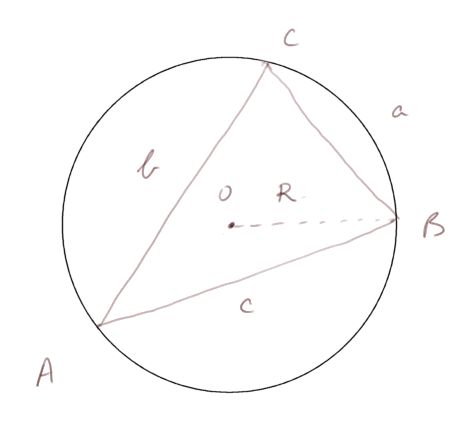
Notre problème est : comment trouver le moyen de lier les côtés a, b et c, les angles, et R ?

 

Appliquons les conseils de George Polya. Commençons par résoudre le problème dans un cas particulier, en espérant que ça nous guidera vers une solution générale.

Considérons donc tout d'abord un triangle rectangle en C.

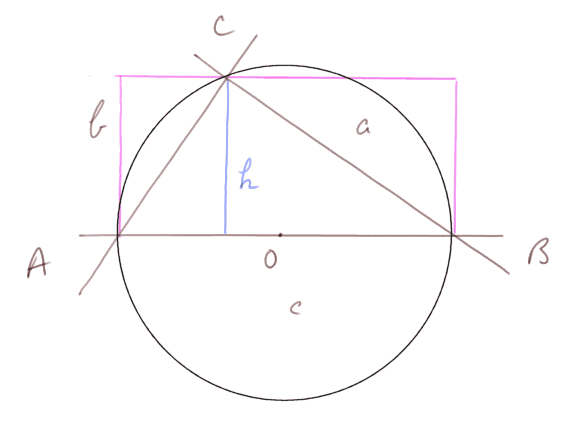
Alors AB est un diamètre du cercle.

On a sinus de l'angle en A = h / b. Donc

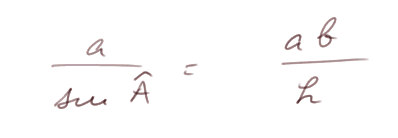
Appelons S la surface du triangle ABC. Alors on a ab = 2S, et aussi h2R = 2S. Donc ab = 2hR. D'où ab / h = 2R.

On peut déplacer le point A sur le cercle sans changer l'angle en A, ni la longueur a.

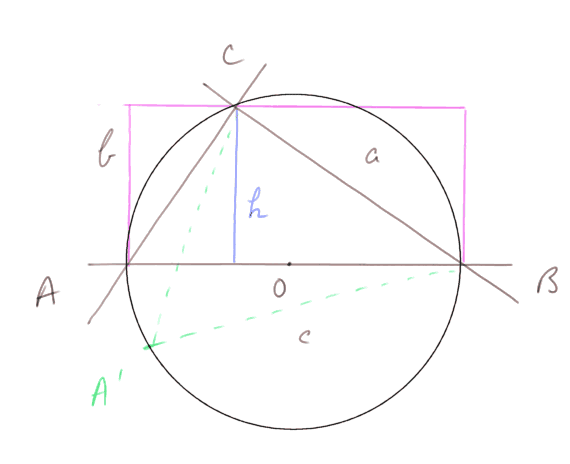
Donc la propriété est vraie où que soit A, c'est-à-dire pour un triangle quelconque. Et elle est vraie aussi en B et en C.

 

Une propriété avancée. Nous allons montrer un résultat étonnant des triangles.

Il a une histoire intéressante. Les Grecs avaient découvert à peu près toutes les propriétés des triangles (même si la trigonométrie, il est vrai, a continué à être développée après eux et que Euler au XVIIIe siècle a trouvé quelques nouveaux résultats). Euclide les avaient exposées dans son célèbre traité de mathématiques. Mais une propriété leur avait échappé. Elle n'a été observée et démontrée qu'en 1898 (!) par le mathématicien américain Frank Morley.

Soit donc un triangle quelconque ABC et les six trisectrices en A, B et C.

On va montrer que le triangle PQR est toujours équilatéral.

 

Démonstration : Notations : nous avons divisé les angles en A, en B et en C, chacun en trois petits angles égaux. Ici on utilise les lettres a, b et c pour ces petits angles (et non plus pour des longueurs de segments).

On a angle en A = 3a, angle en B = 3b et angle en C = 3c. Et donc a + b + c = 60°.

Choisissons aussi une échelle de tout le dessin de telle sorte que le rayon du cercle circonscrit à ABC soit R = 1 (ça ne change rien, et ça allègera les écritures des calculs).

Par la formule des sinus appliquée à ABC, on a l'identité (1)

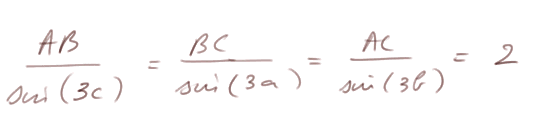
On va se concentrer sur le calcul de la longueur PR, et pour commencer travailler dans le triangle BPC.

Triangle BPC : dans ce triangle, la formule des sinus donne l'identité (2)

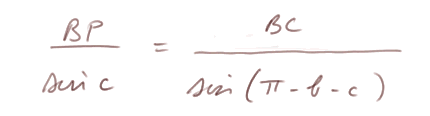
Noter que sin (π - b - c) = sin (b + c). En utilisant (1) et (2) on parvient à

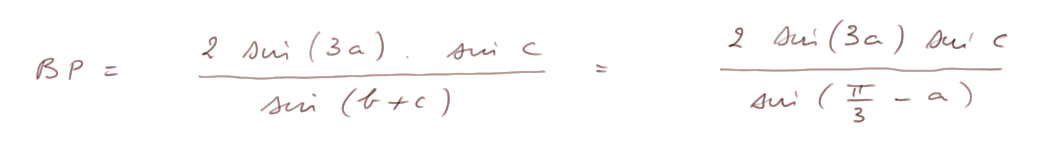
Une identité utile : établissons l'identité suivante

en utilisant plusieurs fois la formule pour le sinus de la somme de deux angles

voici les calculs :

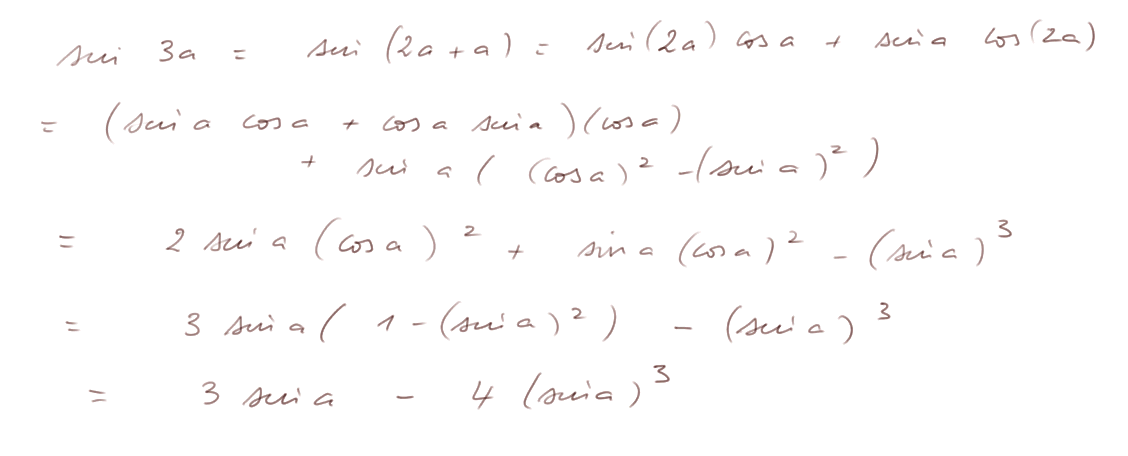
Travaillons maintenant l'expression sin(3a) :

Astuce : On va utiliser l'apparition de π/3 (c'est-à-dire 60°) un peu partout. Notons tout d'abord que 3/4 = [ sin(π/3) ]².

Donc

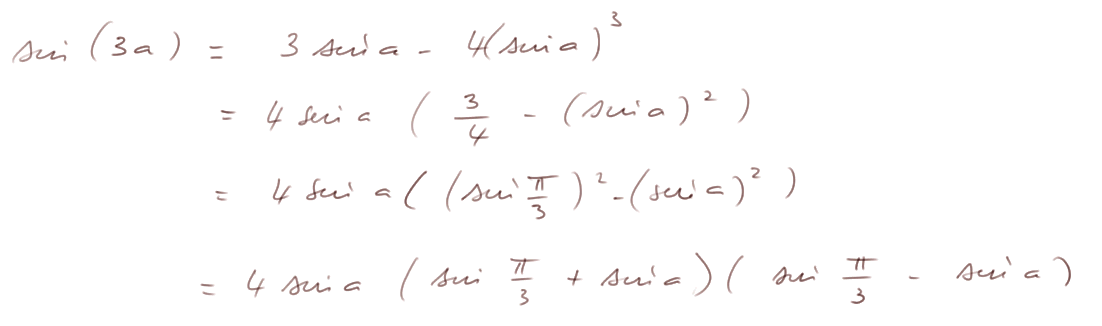
Deuxième astuce : Utilisons

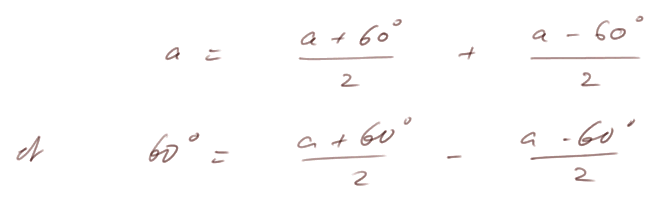
(faire des maths, c'est aussi être créatif, mais avec méthode, cf. conseils de Polya)

Alors on obtient

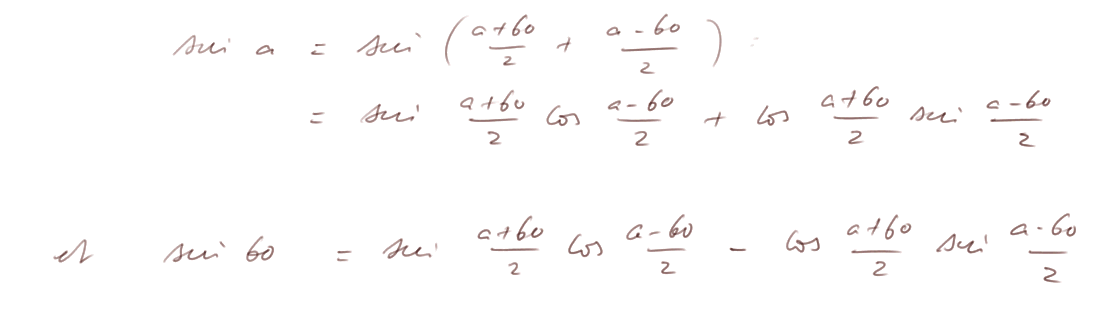
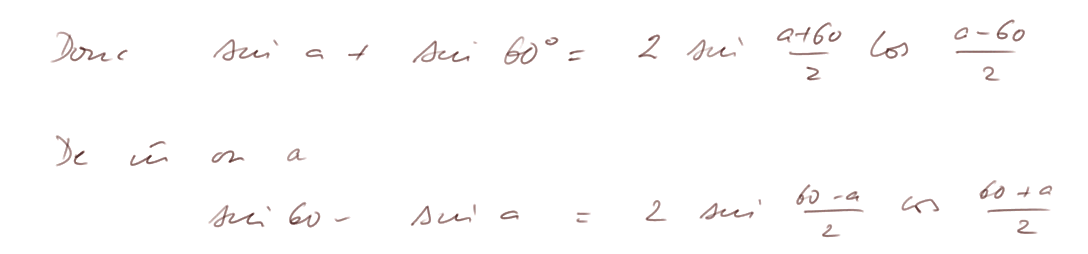
On arrive à

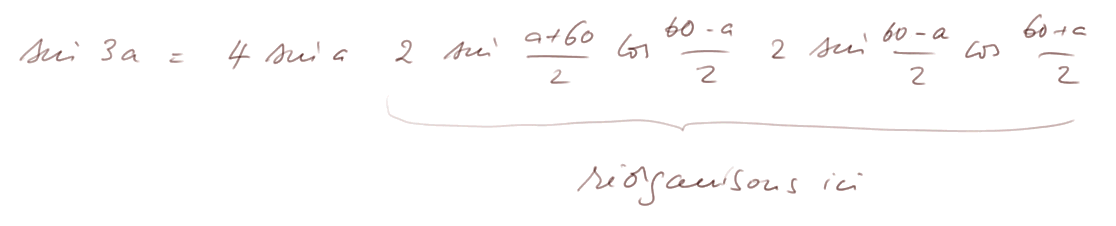
Les termes, après 4sin(a), peuvent être multipliés dans un autre ordre :

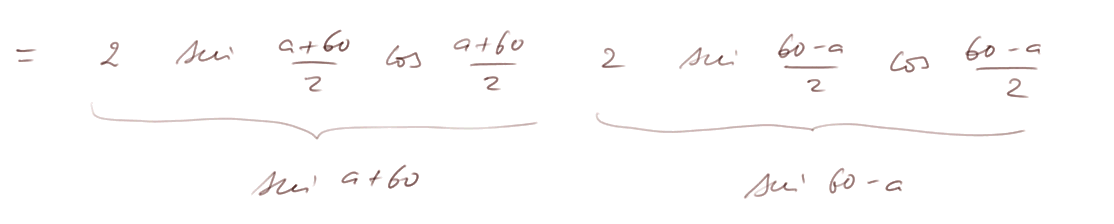
Donc

Rappelons-nous la formule qu'on a calculée pour BP au début de cette démonstration :

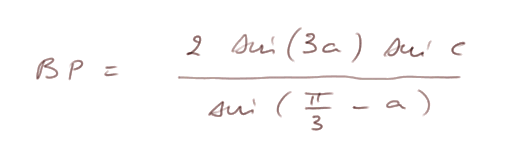
On peut donc maintenant écrire :

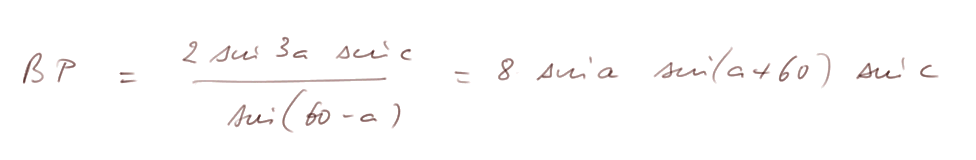
On peut faire les mêmes calculs pour BR, les rôles de a et c sont simplement inversés, donc

 

Nous approchons de la fin de notre démonstration dans ABC et PQR

 

On va maintenant appliquer Al-Kashi (la généralisation du théorème de Pythagore, on a vu cette généralisation en 4e, leçon sur les cosinus et tangentes) au triangle BRP.

PR² = BP² + BR² - 2 x BP x BR x cos(b)

En utilisant à droite nos calculs ci-dessus sur BP et BR, on obtient

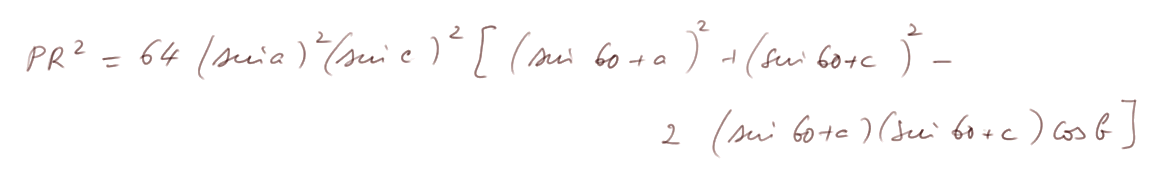
Il nous reste à travailler sur le terme entre crochets.

Notons que a+60, c+60 et b font une somme de 180°, donc on peut dessiner un triangle T avec ces angles. Appelons α, β et γ ses côtés, et prenons-le de dimension telle que son cercle circonscrit ait rayon 1/2.

Alors par la formule des sinus appliquée à T, on a

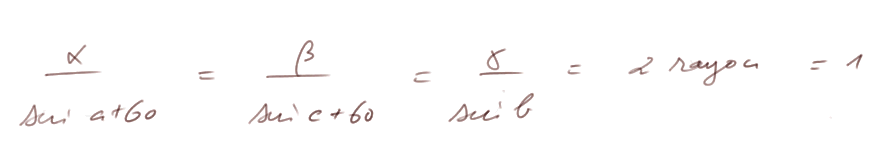
c'est-à-dire

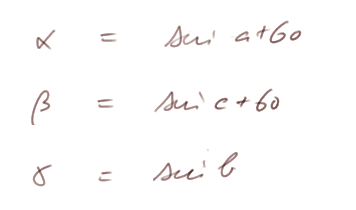
Appliquons Al-Kashi dans le triangle T, au sommet qui a l'angle b :

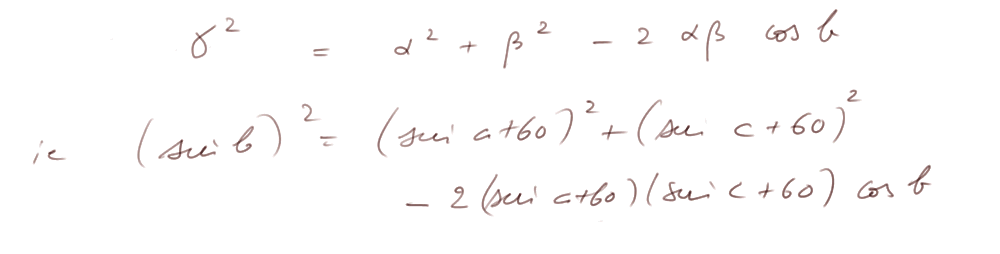
Ce dernier terme est précisément le terme entre crochets dans l'expression de PR².

Nous sommes au bout de nos peines. On a montré que

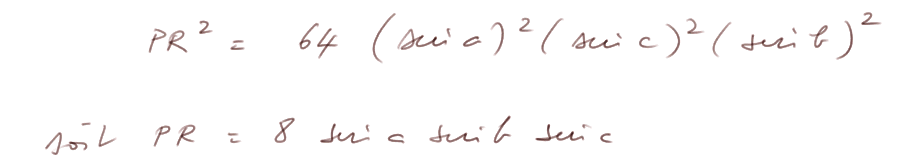
Cette formule étant symétrique en a, b et c, on a la même pour PQ et pour QR.

Donc PQR est équilatéral.

Quod erat demonstrandum.

 

Exercices :

1. Si A = (0 ; 0), B = ( 10 ; 0 ) et C = (6 ; 4 ), quelles sont les coordonnées de P, Q et R ?
2. Vérifier à l'aide de ce solveur que le triangle PQR est équilatéral.

 

Plan général du cours

Contacter le professeur