Cours de mathématiques de 2ndeSimulation de variables aléatoires |
|
Video |
Texte
Pour se familiariser avec les probabilités (avec le modèle qui peut apparaître un peu complexe comportant une expérience
![]() , un univers Ω d'états de la réalité après l'expérience, une mesure de probabilité, des fonctions X, Y ou Z de
Ω vers des ensembles de valeurs possibles, etc.), pour se familiariser avec tout cela, rien de tel que de faire des simulations. Il y a quelques années on n'avait que les dés, les cartes ou les pièces de monnaie pour faire des expériences aléatoires. Maintenant on a les ordinateurs et en particulier, sur les ordinateurs personnels, on a les tableurs avec leurs fonctions =ALEA() et autres.
, un univers Ω d'états de la réalité après l'expérience, une mesure de probabilité, des fonctions X, Y ou Z de
Ω vers des ensembles de valeurs possibles, etc.), pour se familiariser avec tout cela, rien de tel que de faire des simulations. Il y a quelques années on n'avait que les dés, les cartes ou les pièces de monnaie pour faire des expériences aléatoires. Maintenant on a les ordinateurs et en particulier, sur les ordinateurs personnels, on a les tableurs avec leurs fonctions =ALEA() et autres.
On peut simuler à l'aide d'un tableur le jet d'un ou plusieurs dés un grand nombre de fois. Voici un site qui permettait de faire des simulations en ligne : https://www.stat.sc.edu/~west/javahtml/CLT.html. Nous l'avons utilisé pour illustrer le lancer de quelques dés.
En 2016, le site ci-dessus ne fonctionne plus, mais on en trouve beaucoup d'autres sur le Net (recherche lancer de dés interactif en ligne, ou bien online interactive throwing of dice), par exemple https://www.geogebra.org/m/UsoH4eNl
Lancer de 2 dés cinq fois. Soit 2 dés qu'on lance, le résultat du premier est la v.a. X1 et celui du second est la v.a. X2. L'expérience consiste à les lancer tous les deux, et on regarde la v.a. X = X1 + X2.
Techniquement cette expérience est telle que le résultat de X1 n'a aucune influence sur le résultat de X2. C'est un concept important d'indépendance, qu'on étudiera longuement plus tard. Il y a des cas de figures où ce n'est pas vrai. Par exemple si on pioche une personne au hasard dans une population, et qu'on mesure sa taille et son poids, ce sont deux v.a., mais clairement le résultat de l'une donne des informations sur ce que peut être l'autre.
Voici les 5 résultats de X1 + X2 dans notre expérience :
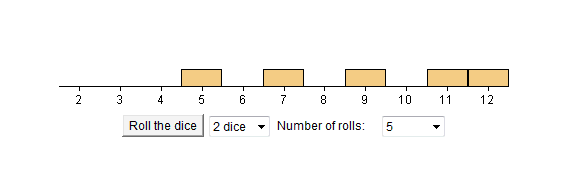
Ici, c'est un hasard, on n'a pas obtenu deux fois le même résultat.
Jet de 2 dés cent fois. Puis on a répété 100 fois l'expérience ![]() consistant à jeter 2 dés. On a compté les résultats dans chaque valeur possible (entre 2 et 12) et dessiné un histogramme.
consistant à jeter 2 dés. On a compté les résultats dans chaque valeur possible (entre 2 et 12) et dessiné un histogramme.
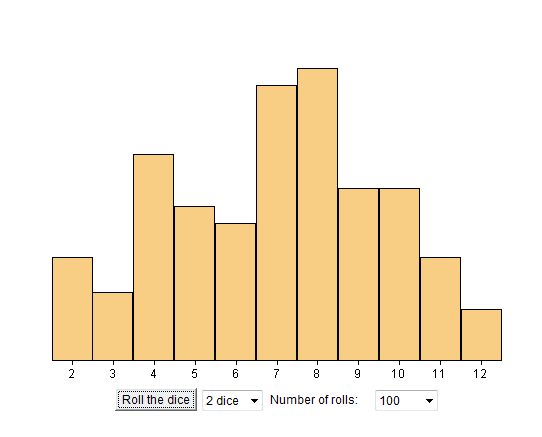
On n'a pas montré sur ce graphique l'échelle des ordonnées : il s'agit d'un axe des comptes, où on a pris une échelle telle que le dessin tienne dans des dimensions raisonnables.
On commence à voir quelle peut être la distribution théorique des probabilités de chaque valeur possible de X1 + X2 mais c'est encore assez approximatif.
Jet de 2 dés 10 000 fois. On sait par une des variantes de la loi des grands nombres que si on produit la v.a. un très grand nombre de fois la fréquence d'observation expérimentale de l'évènement { X1 + X2 = a1 } sera de plus en plus proche de Pr { X = a1 } (où X = X1 + X2)
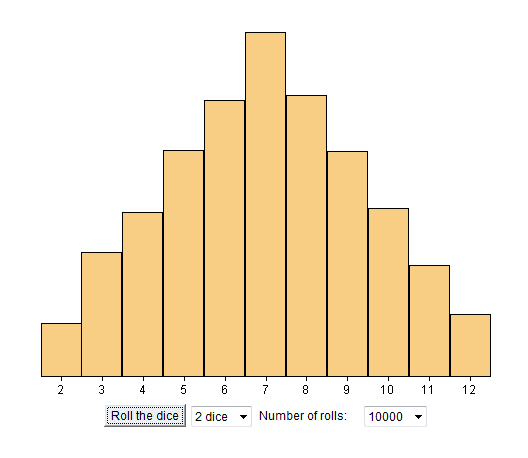
Maintenant les fréquences expérimentales montrées dans cet histogramme sont proches des probabilités théoriques. On obtient donc un beau triangle (pas tout à fait parfait cependant parce qu'il reste expérimental) car il n'est pas difficile de montrer que les probabilités théoriques des onze valeurs possibles (je dis 12 dans la vidéo, par une étourderie) sont
- Pr { X = 2 } = 1/36
- Pr { X = 3 } = 2/36
- ...
- Pr { X = 6 } = 5/36
- Pr { X = 7 } = 6/36
- Pr { X = 8 } = 5/36
- ...
- Pr { X = 12 } = 1/36
et 1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36.
Jet de 5 dés 10 000 fois. L'étude de la somme de 5 dés produit un résultat qui quand on le rencontre pour la première fois est inattendu : l'histogramme des résultats ne tend pas vers une courbe très simple (droite, triangle, etc.) mais vers une courbe en cloche
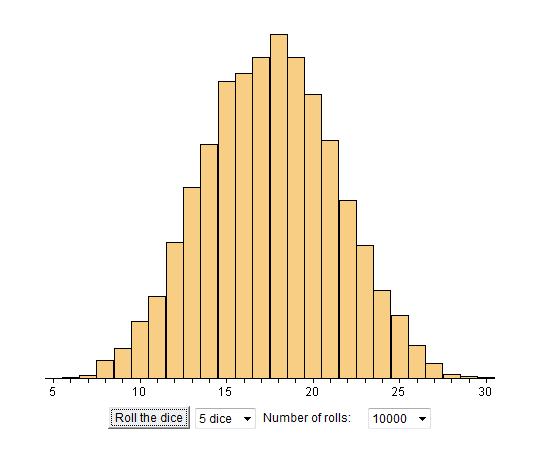
On a donc ici lancé X = X1 + X2 + X3 + X4 + X5 10 000 fois. Et on a compté les résultats expérimentaux de chaque valeur possible qui forment l'ensemble { 5, 6, 7... 29 , 30 }.
On voit que la moyenne de X1 + X2 + X3 + X4 + X5 est 17,5 comme il se doit (car chaque dé a pour moyenne 3,5).
Mais le calcul des probabilités de chaque valeur possible est plus délicat que pour deux dés.
C. F. Gauss (1777 - 1855) est le premier a avoir fait des calculs complets sur ces v.a. sommes de plusieurs autres. Il a montré que dans certaines conditions très naturelles leur distribution de probabilité s'approchait de plus en plus d'une courbe en cloche. Pour cette raison ce genre de courbe (dont nous étudierons l'équation plus tard) s'appelle aussi une courbe de Gauss, ou une gaussienne. Cette famille de courbes a même trois noms car on dit aussi "une loi normale".
Variables aléatoires "Uniforme(0, 1)". On va maintenant produire une variable aléatoire X prenant ses valeurs possibles dans le segment des nombres réels (0, 1) (ou [0, 1], ça ne fait pas de différence).
X est telle que quels que soient "a" et "b" entre 0 et 1 la probabilité que X tombe dans le sous-segment (a, b) de (0, 1) est b-a.
Pour cette raison, une variable aléatoire de ce type est appelée une v.a. Uniforme(0, 1)
On va même s'intéresser à une variable X = U1 + U2 + ... + U8 où chaque Ui est une v.a. Uniforme(0, 1) et les Ui n'ont aucune influence les unes sur les autres.
On va lancer U1 + U2 + ... + U8 5000 fois et compter combien de fois on a
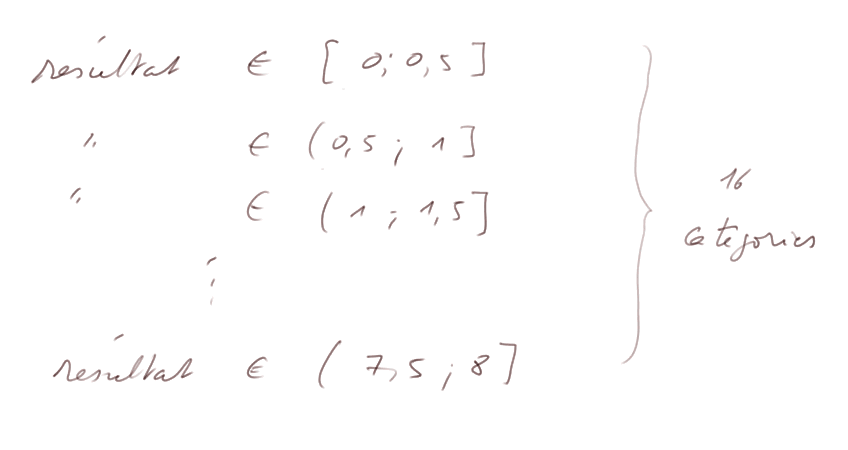
c'est-à-dire qu'on va tracer un histogramme avec le choix des tranches ci-dessus.
Le tableur RV8uniforms.xls permet d'effectuer la simulation. Voici un résultat :
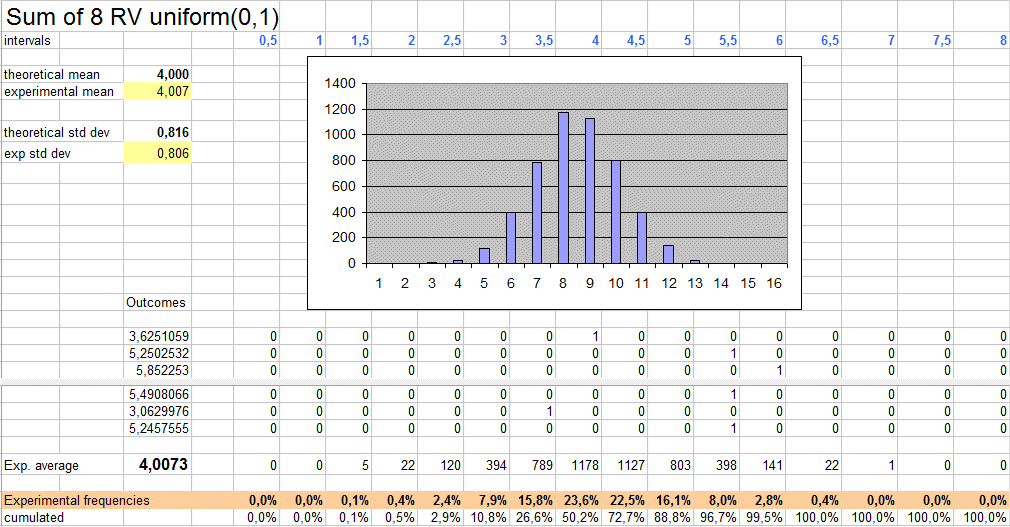
On calcule aisément que la moyenne théorique de X est 4. Et c'est encore assez simple de calculer que son écart type (en anglais, "standard deviation") est 0,816.
On observe que la moyenne expérimentale des 5000 tirages de X est 4,0073 et l'écart type expérimental 0,806. Donc tout va bien.
On observe surtout que l'histogramme des 5000 résultats montre encore une courbe en cloche.
Courbe en cloche. Il s'agit en fait d'une famille de courbes (comme il existe une famille de paraboles d'axe vertical), dépendant de deux paramètres :
- la position du milieu
- l'étroitesse ou au contraire l'évasement de la courbe
Beaucoup de variables aléatoires dans la nature, en Physique et dans d'autres domaines, ont une distribution de probabilité en cloche. C'est la raison pour laquelle c'est une famille de courbes très importante.
Exercices :
- Avec le tableur RV8uniforms.xls regarder comment se comportent la moyenne et l'écart type expérimentaux de X quand on répéte les 5000 lancers de X = U1 + U2 + ... + U8 plusieurs fois. (On lance une nouvelle simulation de 5000 lancers en appuyant sur la touche F9.)