Cours de mathématiques de 2ndeTransformations dans le plan |
|
Video |
Texte
Une transformation dans le plan est une fonction qui à chaque point associe un autre point (qui peut être lui-même). On en a déjà rencontré beaucoup :
- les translations
- les rotations autour d'un point
- les symétries axiales
- et même la transformation (x, y) -> (x, cy) qu'on a utilisée, dans la leçon précédente, pour définir et étudier les ellipses.
Translations. Soit un vecteur V = (a, b), c'est-à-dire un vecteur qui transforme (0, 0) en le point (a, b), alors à tout point (x, y) la translation selon V associe (x + a, y + b).
On a vu que les translations se combinent (on dit "s'additionnent") et que l'opération est commutative. C'est une conséquence des propriétés des parallélogrammes.
Rotations.
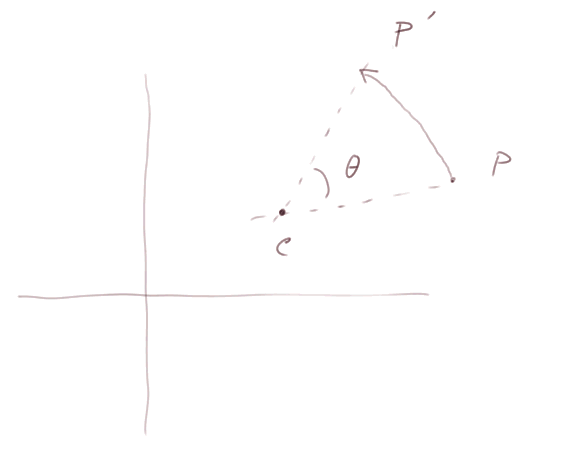
La combinaison de deux rotations de centres différents peut donner une rotation ou une translation. (Et ce n'est pas commutatif.)
Symétries axiales.
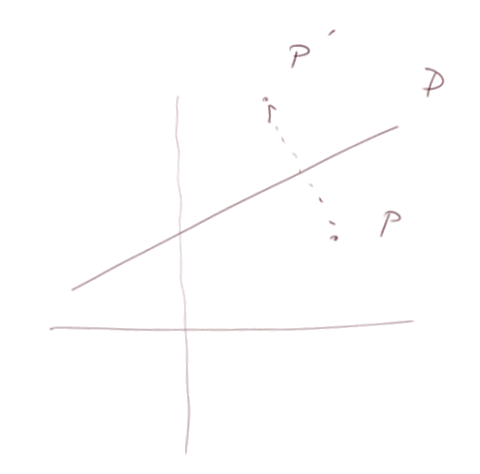
La combinaison de 2 symétries axiales parallèles donne une translation (pas commutatif). Et si elles ne sont pas parallèles ça donne une rotation (pas commutatif non plus).
Symétries centrales. Ce n'est rien de plus qu'une rotation de 180°.

Isométries. On appelle "isométrie" dans le plan une transformation qui préserve les distances.
Si avec la transformation T : A -> A', et B -> B', alors la distance entre A' et B' est la même qu'entre A et B.
Les seules isométries du plan sont les transformations listées ci-dessus, plus la symétrie axiale suivie d'une translation parallèle à l'axe.
Elles préservent toutes les angles, en valeur absolu. On les classe en effet en deux catégories :
- Celles qui préservent le sens des angles : translations, rotations
- Celles qui inversent le sens des angles : symétries axiales, suivies ou non d'une translation
Intuition. Intuitivement, les isométries correspondent au déplacement d'une feuille avec un dessin dessus (translations ou rotations), ou à son retournement suivi ou non d'un déplacement.
Les isométries du plan forment un ensemble structuré : on peut combiner les isométries ; on obtient bien sûr encore une isométrie.
C'est-à-dire que toute combinaison de deux isométries est encore, soit :
- une translation
- une rotation
- une symétrie axiale
- une symétrie axiale + une translation parallèle à l'axe (appelée "symétrie glissée")
Autres transformations. Il existe beaucoup d'autres transformations intéressantes dans le plan ayant une interprétation géométrique simple. Par exemple : les homothéties.
Homothéties.
Une homothétie de centre C et de rapport k est la transformation décrite dans la figure ci-dessous
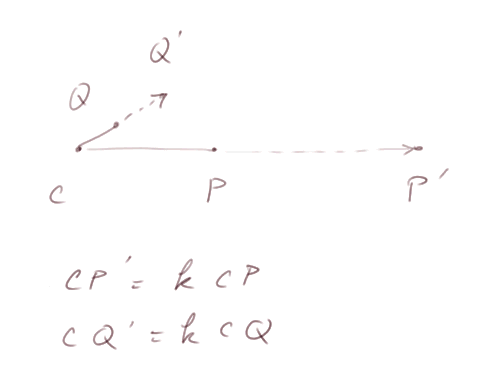
Quelques propriétés des homothéties.
- Préservation des formes. Les homothéties préservent le parallélisme et donc les angles, mais pas les distances. Elles préservent cependant les rapports de longueur, et elles multiplient les surfaces par k2.
A vrai dire, quand k est positif, une homothétie n'est rien de plus qu'une représentation à plus grande (ou plus petite) échelle des figures du plan, autour d'un point central. Et quand k est négatif - ce qu'on appelle une "homothétie négative" - ça revient à une homothétie positive et une rotation à 180°.
- Combinaison d'homothéties. Soit H l'homothétie [ C, k ] et H' l'homothétie [ C', k' ], alors la combinaison H' ○ H donne :
- soit une translation si kk' = 1
- soit, si kk' est différent de 1, une homothétie de rapport kk', avec pour centre un point C'' situé sur la droite CC'.
Il existe des transformations qui transforment les droites en courbes, et ne préservent pas les distances, mais qui préservent les angles là où les courbes se croisent. On les appellent les "transformations conformes". Par exemple :
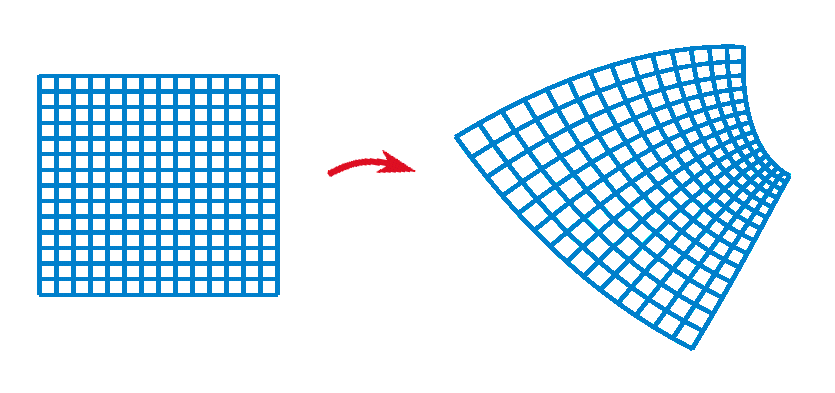
source : wikipedia en anglais
Nous étudierons quelques autres transformations intéressantes dans les années qui viennent.
Pour aller plus loin : voici un résultat "de bon sens" mais dont la démonstration nécessite des mathématiques plus avancées que celles du lycée :
Toute transformation f continue d'un disque fermé dans lui-même a au moins un point fixe (c'est-à-dire dont le transformé est lui-même).
(fermé veut dire "qui contient le cercle qui est son bord" ; continue veut dire que "quand une suite de points du disque tend vers un point limite, alors la suite des transformés tend vers le transformé du point limite").
Exercices :
- Démontrer qu'une rotation suivie d'une translation est encore une rotation de même angle, mais avec un autre centre.
- Démontrer la dernière propriété mentionnée sur les homothéties.