Cours de mathématiques de 3e Factorisations et racines des polynômes, théorème de Descartes
Video

Texte

Nous avons déjà rencontré des expressions littérales comme

• ax + b
• ax² + bx + c

Elles s'appellent respectivement

• polynôme de degré 1 en x
• polynôme de degré 2 en x, dit aussi "trinôme"

D'une manière générale, l'expression littérale

(où tous les a_i sont des nombres et a_n est différent de zéro) s'appelle un polynôme de degré n de la variable x.

Il est intéressant de considérer différents cas pour les coefficients a_i :

• cas où les a_i sont des entiers relatifs, c'est-à-dire appartiennent à Z
• cas où les a_i sont des nombres rationnels, c'est-à-dire appartiennent à Q
• cas où les a_i sont des nombres réels, c'est-à-dire appartiennent à R
• autres cas

L'ensemble des polynômes se comporte un peu comme l'ensemble des nombres entiers avec les opérations + et x (c'est-à-dire l'addition et la multiplication) : à la décomposition unique des nombres entiers en facteurs premiers correspond la factorisation unique des polynômes en polynômes "irréductibles".

Nous n'étudierons pas l'ensemble des propriétés des polynômes à coefficient dans un ensemble donné. C'est un sujet pour le lycée et après, mais nous allons étudier un résultat simple et puissant : le théorème de Descartes (1596 - 1650). Descartes a fait des travaux importants en mathématiques, en physique et en philosophie. (Il y a beaucoup de résultats dus à Descartes en mathématiques et en optique, et il a écrit parmi d'autres ouvrages le célèbre "Discours de la Méthode", une sorte de précurseur de Polya !)

Théorème de Descartes : si P(x) est un polynôme, et r en est une racine, alors le polynôme peut être factorisé sous la forme

P(x) = (x - r)Q(x)

où Q(x) est un polynôme de degré inférieur à celui de P.

On savait évidemment l'inverse : si P(x) peut être écrit sous la forme (x - r)Q(x), alors P(r) = 0. C'est-à-dire r est une racine de P.

Le théorème de Descartes est l'autre sens. Exemple :

4 est une racine du polynôme 5x² - 19x - 4. Alors 5x² - 19x - 4 peut être écrit sous la forme (x - 4)Q(x). Ici il n'est pas trop difficile de voir que Q(x) = 5x + 1.

Démonstration du théorème de Descartes :

Elle s'appuie sur une jolie identité remarquable que nous connaissons déjà (sous une forme un peu plus simple ) :

On l'a déjà rencontrée, avec r = 1, et "a" à la place de "x". Celle-ci se démontre exactement de la même façon : développer le produit à droite, et voir que tous les termes s'annulent sauf le premier et le dernier.

Soit donc un polynôme

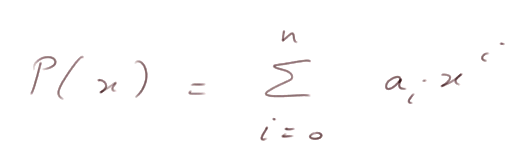
(Le signe sigma veut dire "somme" et il faut sommer pour toutes les valeurs de i, nombre entier variant entre 0 et n. C'est une façon plus simple de noter la somme a₀ + a₁x + a₂x² + ... + a_nxⁿ)

et supposons que r est une racine de P, c'est-à-dire P(r) = 0

(sans utiliser le signe sigma, ça veut dire a₀ + a₁r+ a₂r² + ... + a_nrⁿ = 0)

On peut donc écrire P(x) = P(x) - P(r), puisque ça consiste à retrancher zéro.

Or P(x) - P(r) =

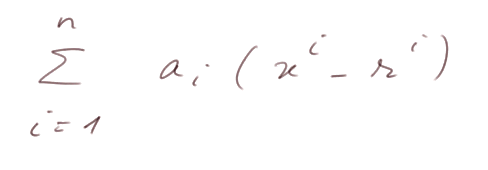
et chacun des termes (xⁱ - rⁱ) peut être écrit sous la forme (x - r)Q_i(x), où chaque Q_i(x) est un polynôme donné par l'identité mentionnée au début de la démonstration.

Donc on peut factoriser (x - r) et écrire :

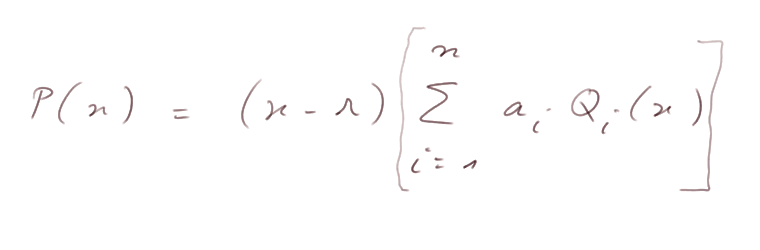
C.Q.F.D.

(Ça veut dire : "ce qu'il fallait démontrer.")

Application : un polynôme de degré 3 (c'est-à-dire une expression littérale de la forme a₃x³+ a₂x² + a₁x+ a₀) est toujours factorisable sous la forme

(x - r)(ax² + bx + c)

Pourquoi ? Eh bien, quand on trace les points [ x ; a₃x³+ a₂x² + a₁x+ a₀ ], on a une courbe qui descend vers - ∞ quand x devient très petit (vers - ∞ ; je fais l'hypothèse que a₃ est positif), et qui s'élève vers + ∞ quand x devient très grand (vers + ∞). Donc elle croise forcément l'axe des x (c'est-à-dire la droite de tous les points d'ordonnée 0).

Exemple : traçons [ x ; x³+ 2x² - 5x + 8 ]

 

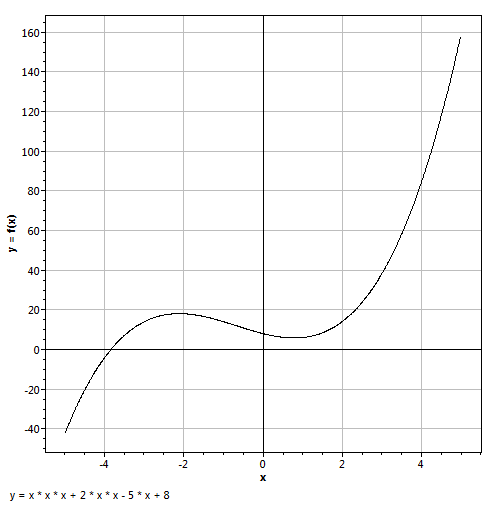
Il y a donc toujours au moins une racine (parfois trois). C'est-à-dire, d'après le théorème de Descartes, un polynôme du troisième degré est toujours factorisable au moins en

(x - r)(ax² + bx + c)

(Le trinôme qui reste peut ne pas être factorisable, tout dépend de son discriminant.)

Dans l'exemple ci-dessus, x³+ 2x² - 5x + 8 est factorisable avec ≈ (x + 3,8).

 

Exercices :

1. Factoriser x³+ 1
   
   

 

Plan général du cours

Contacter le professeur