Cours de mathématiques de 3e Arithmétique : diviseurs, PGCD et algorithme d'Euclide
Video

Texte

Un nombre entier n quelconque a des diviseurs, au minimum 1 et lui-même, parfois beaucoup d'autres entre les deux :

• 37 n'a pour diviseurs que 1 et 37 (c'est un nombre premier).
• 24 a pour diviseurs 1, 2, 3, 4, 6, 8, 12 et 24.

On peut écrire 24 = 2 x 12 = 3 x 8 = 4 x 6. Une fois qu'on connaît tous les diviseurs jusqu'à la racine carrée de n et qu'on connaît les quotients correspondants, on les connaît tous, car si n = a x b, soit a, soit b est plus petit ou égal à racine de n.

Regardons la décomposition 24 = 2 x 12.
12 = 2 x 6 et
6 = 2 x 3

Donc on a aussi 24 = 2 x 2 x 2 x 3. On a vu que les produits a x b peuvent être rangés en rectangles de petits cailloux dans le plan, et les produits a x b x c peuvent être rangés en parallélépipèdes rectangles dans l'espace. Eh bien on peut penser à 2 x 2 x 2 x 3 comme à des petits cailloux rangés en hyper-parallélépipède dans l'espace à 4 dimensions (voir leçon précédente sur le jeu de tic tac toe dans l'espace).

Si on part de 24 = 3 x 8, on voit aussi que 24 = 3 x 2 x 2 x 2, c'est-à-dire la même décomposition à l'ordre près des facteurs. Si on part de 24 = 4 x 6, comme 4 = 2 x 2 et 6 = 2 x 3, on tombe encore sur 24 = 2 x 2 x 2 x 3.

Nous verrons plus tard que la décomposition d'un nombre entier quelconque en facteurs premiers est unique.

• 37 = 1 x 37
• 24 = 2 x 2 x 2 x 3

Tournons-nous maintenant vers ce qu'on appelle le plus grand commun diviseur (pgcd) de deux nombres.

Le plus grand commun diviseur de deux nombres entiers a et b (avec mettons a < b), c'est, comme son nom l'indique, le plus grand nombre entier c qui divise à la fois a et b.

Cas particuliers :

• si a divise b, alors pgcd (a, b) = a
• si b est premier, alors pgcd (a, b) = 1

Exemples de pgcd :

• pgcd (20, 25) = 5
• pgcd (7, 14) = 7
• pgcd (12, 15) = 3
• pgcd (42, 56) = 14

Il y a une propriété importante des pgcd, liée à la division euclidienne, qui va nous permettre de trouver rapidement le pgcd de deux nombres a et b. Soit donc deux nombres a et b (avec a < b), si la division euclidienne de b par a est b = n x a + c, alors le pgcd de a et b est aussi le pgcd de a et c.

En effet tout nombre d qui divise a et b divise aussi b - n x a = c. Et tout nombre qui divise a et b - n x a divise aussi a et b.

 

 

Ceci nous conduit à l'algorithme d'Euclide : pour trouver le pgcd de a et b (où a < b),

1. faire la division euclidienne de b par a, b = n x a + c
2. si le reste "c" est égal à zéro, a est le pgcd de a et b
3. sinon recommencer l'étape 1 avec a et c, a = m x c + d

Si d = 0, "c" est le pgcd de a et c, et donc aussi de a et b. Si d ≠ 0, recommencer l'étape 1 avec c et d, etc.

Pour résumer, on fait une série de divisions euclidiennes, d'abord b par a, puis "a" par le reste "c", et ainsi de suite. Le dernier reste non nul est le pgcd de a et b.

Exemple 1 : prenons a = 20 et b = 25.
25 = 1 x 20 + 5
et 20 = 4 x 5 + 0.
Donc 5 est le pgcd de 20 et 25.

Exemple 2 : cherchons le pgcd (24, 36)
36 = 1 x 24 + 12
24 = 2 x 12 + 0
Donc 12 est le pgcd de 24 et 36.

Les pgcd sont très utiles pour simplifier les fractions "au maximum". En effet considérons la fraction a/b où a et b sont des entiers positifs (il n'est plus nécessaire que a soit inférieur à b, il peut aussi être égal ou plus grand). Si q est le pgcd de a et b, alors a = n x q, et b = m x q. Donc on peut simplifier la fraction par q. On obtient a/b = n/m. Et n/m n'est plus simplifiable, car il n'y a plus de diviseur commun (autre que 1) entre n et m. S'il y en avait encore, q n'aurait pas été le pgcd de a et b.

Quand n et m n'ont pas de diviseurs communs (comme par exemple 14 et 15) on dit qu'ils sont "premiers entre eux".

Exemple de simplification d'une fraction :

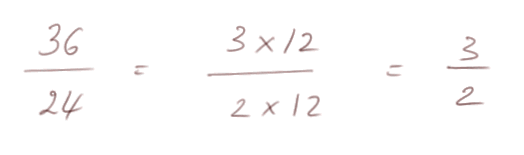
Exercices

1. Trouver le pgcd de 58 et 24

Réponses

 

Plan général du cours

Contacter le professeur

 

 

Réponses : 58 = 2 x 24 + 10 et 24 = 2 x 10 + 4 et 10 = 2 x 4 + 2, et 4 = 2 x 2 + 0. Donc pgcd(58, 24) = 2