Cours de mathématiques de 4eLes puissances d'un nombre a |
|
|
|
|
Video |
|
Texte
Les puissances que nous avons définies pour 10 peuvent être définies pour n'importe quel nombre a. On se limitera tout d'abord à des nombres a positifs. Prenons un nombre a quelconque (positif), par exemple 7/3 si on veut fixer les idées.
a x a = a2 on lit "a puissance deux", ou "a au carré", parfois simplement "a deux"
a x a x a = a3 on lit "a puissance trois", ou "a au cube", parfois simplement "a trois".
On observe, comme pour 10, que a2 x a3 = a5, et plus généralement an x am = an + m.
On définit naturellement a-1 comme étant 1/a. Ainsi on a an x a-1 = an - 1. De même a0 = 1. Ainsi an x a0 = an + 0= an.
Bref on est en train de créer toute une arithmétique des nombres entiers avec les exposants de a. L'étape suivante naturellement est de passer aux fractions, exactement comme on a créé les fractions au milieu des nombres entiers.
On va définir a1/2 comme le nombre tel que a1/2 x a1/2 = a. Pour certains a c'est un entier. Par exemple, si a = 16, a1/2 = 4.
N'est-ce pas aussi -4 ? On conviendra, par convention, que si a est positif, a1/2 est la valeur positive telle que a1/2 x a1/2 = a.
La plupart du temps, a1/2 n'est ni un nombre entier, ni même une fraction. Ce n'est pas grave, c'est un nouveau nombre. On a l'habitude ! Il sera positionné sur la droite des nombres, comme nous l'avons déjà fait pour les entiers et les fractions.
Mais autant une fraction ne peut pas être "approchée par des nombres entiers", autant on pourra toujours approcher un nombre du genre a1/2 aussi près qu'on veut par des nombres rationnels.
Comme on vient de le dire, on peut toujours approximer a1/2 avec une fraction, et même un nombre décimal. Prenons a = 10. Alors a1/2 est tel que a1/2 x a1/2 = 10. Donc 3 < a1/2 < 3,2 car 32 = 9 et 3,22 = 10,24.
Avant de continuer à approximer 101/2, rappelons que a1/2 a une notation consacrée, c'est

On lit "racine carrée de a", ou simplement "racine de a".
Continuons à approximer racine de 10. On a vu que c'est entre 3 et 3,2. Alors on prend la moyenne de ces deux nombres, c'est-à-dire 3,1, et on divise 10 par 3,1. On tombe sur 3,225... On prend la moyenne de 3,1 et 3, 225 : c'est 3,1625. Et on divise 10 par 3,1625. On obtient 3,162055. On prend la moyenne de 3,1625 et 3,162055 : c'est 3,162277... Et ainsi de suite.
Si on prend notre calculette, qui en général a une touche "racine carrée", on trouve que racine de 10 = 3,162277... Donc le procédé ci-dessus, dû à Héron d'Alexandrie (c. 10, c. 70), est très efficace.
On définit de la même manière a1/3 que l'on note
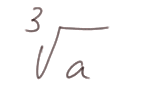
On le lit "racine cubique de a".
C'est le nombre tel que a1/3 x a1/3 x a1/3 = a. Par exemple la racine cubique de 27 est 3, car 3 x 3 x 3 = 27.
La racine cubique de 10 est 2,1544346... Je l'ai obtenue à l'aide d'un tableur sur un ordinateur. Dans la plupart des tableurs le signe pour "puissance" est ^.
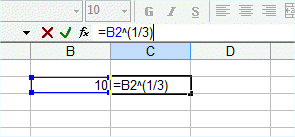
Le cacul ci-dessus donne dans la cellule C2 la racine cubique du nombre qui est dans la cellule B2. Ici on a 10 dans B2, et donc le résultat dans C2 est 2,1544346... A l'aide d'un tableur comme ceci, on peut calculer toute une série de puissances d'un nombre a donné et construire une représentation graphique, comme on en a déjà fait un certain nombre.
On définit aussi a2/3 : c'est la racine cubique de a2. On vérifie que c'est aussi le carré de a1/3, c'est-à-dire a1/3 x a1/3. Donc il n'y a pas d'ambiguité dans l'écriture a2/3. Par exemple la puissance 2/3 de 10 est 4,641588...
On définit enfin an/m quels que soient les nombres entiers, positifs ou négatifs, n et m (ne pas oublier que a-p = 1 / ap).
Généralement, il nous faudra un ordinateur ou une calculette scientifique pour calculer an/m, ou des techniques d'approximation.
De toute façon dans un premier temps nous n'utiliserons que les puissances entières et les racines carrée et cubique.
Exercices
- Avec la méthode de Héron calculer racine de 2.
Plan général du cours
Contacter le professeur
Réponses : vous devez trouver 1,414213...