Cours de mathématiques de 4e Théorème de Pythagore Biographie de Pythagore
Video

Texte

Nous arrivons à un résultat fondamental de la géométrie dans le plan : le théorème de Pythagore. Avec le théorème de Thalès, et quelques autres, il fait partie des outils mathématiques qu'on utilise dans la vie de tous les jours. Toute personne qui a reçu une instruction primaire et secondaire doit connaître et savoir utiliser ce théorème.

Avant d'arriver au théorème, rappelons que dans tout triangle ABC, on a longueur de BC ≤ AB + AC.

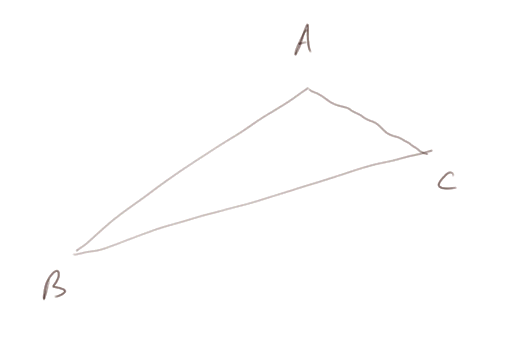
C'est vrai même si le triangle est rectangle.

Mais dans un triangle ABC, rectangle en A, on a la relation "magique" suivante : BC² = AB² + AC².

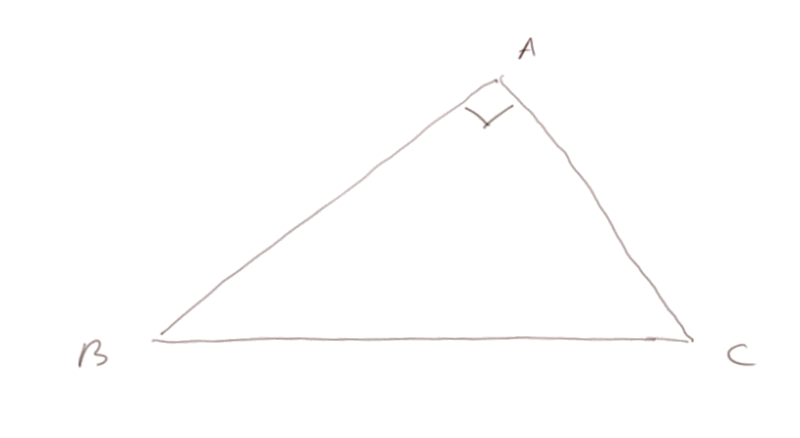
L'énoncé habituel du théorème de Pythagore dit : "Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés."

(BC, le grand côté, s'appelle "l'hypoténuse".)

Il existe beaucoup de démonstrations élémentaires. Regardons-en une. On va appeler "a" la longueur du côté BC, "b" la longueur du côté AC, et "c" la longueur du côté AB.

L'idée est de "compléter" la figure représentant le triangle ABC avec deux carrés, comme ceci dessous.

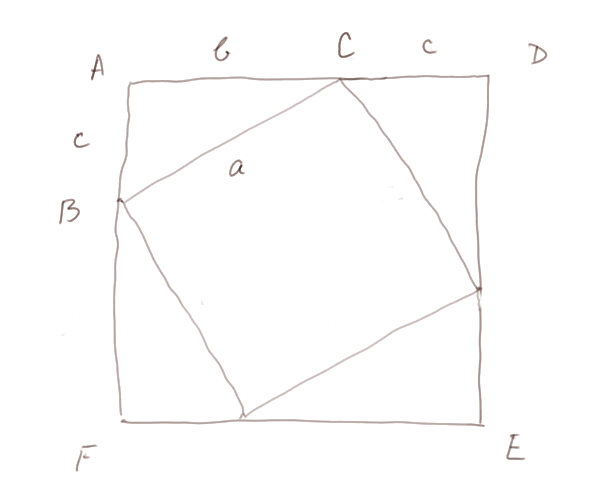
Un peu comme dans un puzzle, quatre copies de ABC posées sur les bords du carré central (de côté "a"), forment le grand carré ADEF.

Maintenant on va calculer la surface (= aire) du grand carré de deux manières différentes. D'une part c'est (b + c)². D'autre part, c'est la surface du carré intérieur plus 4 fois la surface du triangle ABC, c'est-à-dire a² + 4 fois bc/2.

Donc on arrive à l'identité (b + c)² = a² + 2bc. On développe comme on a appris à le faire le produit à gauche du signe égal. On obtient b² + 2bc + c² = a² + 2bc. On retire de chaque côté 2bc (ce qui ne change rien à l'identité). Donc finalement, dans tout triangle rectangle, on a forcément

a² = b² + c²

Pour certaines longueurs entières de AB et AC, l'hypoténuse a aussi une longueur entière. Exemples

• Si b = 3 et c = 4, alors a = 5. C'est l'exemple le plus connu. Et il faut le retenir.
• b = 5 et c = 12 -> a = 13
• b = 12 et c = 35 -> a = 37

Il existe une infinité de tels triplets.

Mais en général, même si b et c sont des longueurs en nombre entiers, a ne l'est pas. Et "a" n'est même pas, en général, une fraction. L'exemple le plus connu, qui avait tant perturbé Pythagore, est b = c = 1 -> a = racine de 2. Racine de 2 ne peut pas être une fraction, nous verrons cela en 3e.

Les Anciens, bien avant Pythagore (c. -580, c. -497) connaissaient déjà le théorème de Pythagore, ou du moins beaucoup de cas particuliers. Ils étaient fascinés par les triplets entiers. Il existe une tablette mésopotamienne, dite tablette de Plimpton, qui donne toute une liste de paires de nombres, chaque fois début de triplets entiers satisfaisant a² = b² + c². Elle date de 1800 avant J.-C. Et les résultats qu'elle présente remontent sans doute à -2000 av. J.-C.

 

 

Pour terminer cette leçon, méditons sur les mathématiques avancées, en parlant du Grand Théorème de Fermat (c. 1605, 1665). Pierre de Fermat était un mathématicien du début du XVIIe siècle qui vivait dans le Sud-Ouest de la France. Ce théorème énonce que l'équation a² = b² + c² a beaucoup de solutions sous forme de triplets de nombres entiers, mais dès que l'exposant est ≥ 3, les seules solutions en nombres entiers sont celles sans intérêt où b ou c = 0 et a est égal à l'autre nombre non nul.

La recherche de la solution de ce théorème, que Fermat a énoncé mais dont il n'a pas donné de démonstration, a occupé les plus grands mathématiciens pendant plus de 3 siècles. Il a finalement été démontré en 1995. Les nombreuses tentatives pour essayer de le prouver ont fait beaucoup progresser les mathématiques.

La démonstration finalement trouvée utilise des mathématiques de haut niveau (que l'on peut atteindre après une dizaine d'années d'études supérieures en mathématiques) et elle a même créé des nouvelles branches des mathématiques de haut niveau.

Les mathématiques de haut niveau semblent ne servir à rien, et être seulement un sujet d'admiration (comme on admire, selon ses goûts artistiques, la Joconde ou Les demoiselles d'Avignon) de la part des esprits sensibles à leur genre de beauté. Mais la physique de haut niveau parfois les utilisent. L'inverse est vrai aussi : il arrive que la physique fondamentale crée, pour expliquer des expériences, des structures de nature mathématique que les mathématiciens reprennent ensuite et incorporent à leurs propres travaux.

La physique fondamentale semble elle aussi ne pas servir à grand chose. Il y a à Genève un nouvel appareil, qui a coûté plus de 5 milliards d'euros à construire, appelé le Large Hadron Collider (LHC) et qui va investiguer les propriétés de la matière à l'échelle de fractions d'atomes. A quoi cela peut-il servir ? Cependant la physique de haut niveau conduit à des applications, heureuses ou malheureuses : des technologies qui améliorent notre cadre de vie (comme les baladeurs mp3 qui contiennent des milliers de chansons dans le volume d'un morceau de sucre), mais aussi des armements terriblement efficaces.

Science et armement : on peut le regretter mais force est de constater que la guerre est une grande source de progrès scientifiques, par exemple usage de la poudre à des fins militaires (au début du XIVe siècle en Occident), ordinateurs (issus de la Seconde Guerre mondiale), Internet (créé par le Département de la Défense américain en 1969), etc.

On peut discuter de l'amélioration réellement apportée par ces technologies. On se sent parfois submergé par elles. Mais nous sommes en train d'apprendre les mathématiques sur Internet, de manière confortable, comme on n'aurait pas pu le faire vers 1980 ou même 1990.

Exercices :

1. Utiliser le théorème de Pythagore plusieurs fois pour trouver la longueur de la diagonale d'un cube de côté 1 mètre.

Réponses

 

Plan général du cours

Contacter le professeur

 

 

Réponse : Racine de 3 = 1,732... mètre.