Cours de mathématiques de 5e Cercles, Pi et Ellipses
Video

Texte

Le cercle est la figure dans un plan formée par tous les points à égale distance d'un point donné. Le point donné s'appelle le centre du cercle, et la distance donnée s'appelle le rayon du cercle.

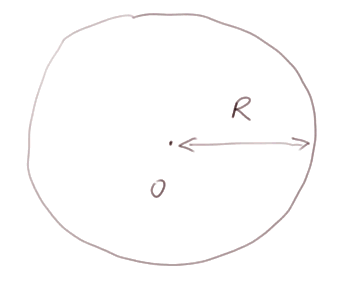
Il y a une infinité de cercles dans le plan, puisqu'on peut choisir le centre et le rayon.

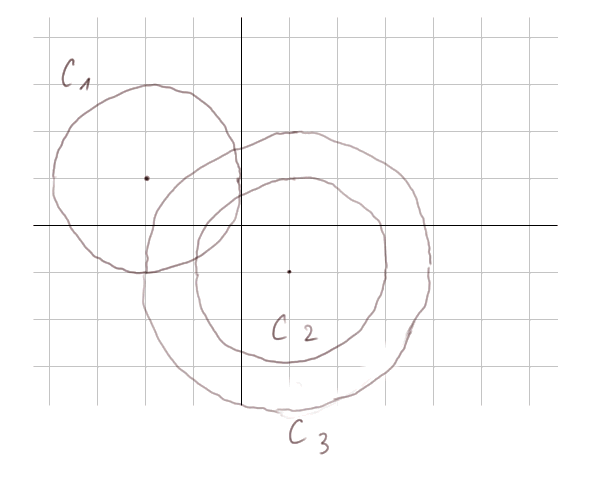
Voici trois exemples de cercles :
C₁ a pour centre le point de coordonnées (-2 ; 1) et pour rayon 2 centimètres,
C₂ a pour centre le point de coordonnées (1 ; -1) et pour rayon 2 centimètres,
C₃ a pour centre le point de coordonnées (1; -1) et pour rayon 3 centimètres, on dit qu'il est concentrique au deuxième cercle.

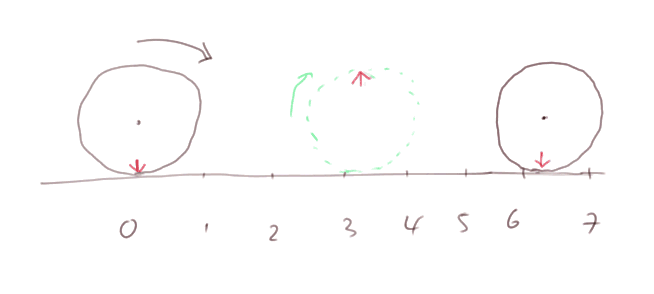
Longueur de la circonférence d'un cercle : imaginons une roue de diamètre 2 cm, posée sur une règle graduée, avec une marque sur le cercle au point où il touche la règle. Faisons-la tourner le long de la règle jusqu'à ce que la marque rouge revienne en bas toucher la règle. A ce moment-là le cercle sera à la position approximative 6,28 centimètres.

Le nombre pi (noté aussi avec la lettre grecque π) est défini comme le rapport entre la circonférence du cercle et son diamètre. On n'a pas besoin de préciser quel cercle, car ce rapport est le même pour tous les cercles. Si L est la circonférence et D le diamètre (et R le rayon, c'est-à-dire D/2), on a

L = π D = 2 π R

π fait environ 3,14.

Pi ne peut pas être représenté exactement par une fraction (c'est un résultat mathématique important), mais il est bien approché par des fractions.

Tout d'abord 3,14 (qui est la même chose que 314/100) fait une erreur de seulement 0,05% par rapport à la vraie valeur de pi.

22/7 fait une erreur de 0,04%

et 355/113 fait une erreur de 0,000008%

Profitons-en pour réviser la lecture des pourcentages : 1% = 1/100 = 10/1000

Donc 0,5% = 5/1000 et 0,05% est la même chose que 5 parties pour 10000.

0,000008% est égal à 8 dixièmes de 0,00001%. Et 0,00001% est la même chose qu'une partie pour 10 000 000. Donc la fraction 355/113 est une approximation plutôt précise de pi. Elle était connue du grand mathématicien grec Archimède (c. -287, -212), qui a malheureusement été tué par un soldat romain durant la Deuxième Guerre punique qui opposait Rome à Carthage.

Le nombre pi joue un rôle très important en mathématiques. Il surgit dans les circonstances les plus inattendues. Par exemple si on regarde la somme 1 -1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 - etc., en allant très loin on s'approche de plus en plus de π/4.

Deuxième exemple : on regarde la somme 1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/49 + etc. (en rajoutant chaque fois la fraction suivante de la forme 1 / n x n ), eh bien on s'approche de plus en plus de π x π / 6.

Et il y a un très grand nombre d'autres exemples.

 

 

Tournons-nous maintenant vers les ellipses, dont les cercles sont des cas particuliers (un peu comme les carrés sont des cas particuliers des rectangles). Nous avons déjà rencontré les ellipses, dans l'espace, comme l'intersection d'un cône et d'un plan.

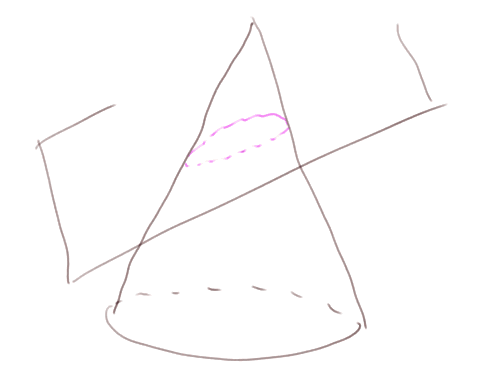
L'ellipse (enfin, la famille des ellipses) est aussi la courbe dans le plan formée par tous les points dont la somme des distances à deux points fixes A et B est constante.

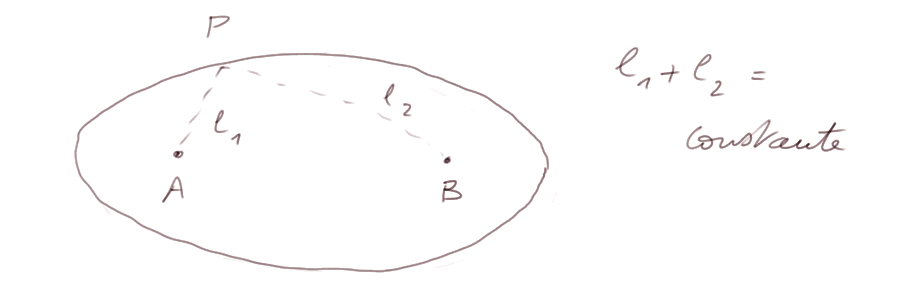
Les points A et B s'appellent les foyers de l'ellipse. On peut dessiner une ellipse en plantant deux clous dans une planche et à l'aide d'une ficelle fermée formant une boucle (sa longueur restera alors l₁ + l₂ + AB) et d'un crayon tracer tous les points avec la ficelle tendue.

Le cercle est un cas particulier de l'ellipse où A et B sont confondus. Et d'ailleurs avec la planche et la ficelle ci-dessus, si on ne prend qu'un seul clou (c'est-à-dire "deux clous confondus" au même endroit) on obtient un cercle.

Les planètes du système solaire décrivent des ellipses dont le soleil est un des foyers. Ça a été compris pour la première fois à l'aide de mesures très précises faites par l'astronome danois Tycho Brahé (1546 - 1601) et analysées par l'astronome allemand Johannes Kepler (1571 - 1630) qui était aussi un peu astrologue. Et ça a marqué le début de progrès importants en mathématiques au XVIIe siècle. Pour certaines planètes, dont la Terre, ce sont de très grandes ellipses dont les deux foyers sont relativement proches, si bien que les trajectoires ressemblent presque à des cercles.

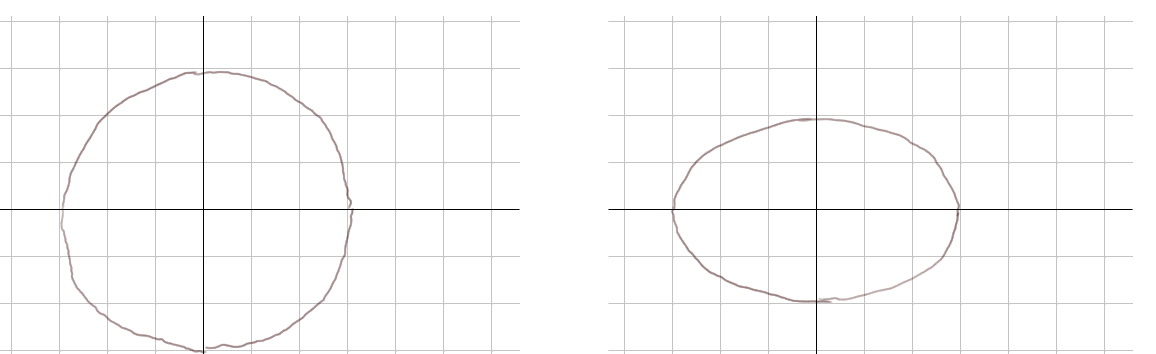
Finissons avec une dernière propriété des ellipses. Ce sont aussi les courbes obtenues à partir de cercles en les aplatissant de la manière précise suivante : tracer un cercle dans un répère du plan, par exemple de centre (0 ; 0) et de rayon 3 centimètres. Puis pour chaque point du cercle réduire la coordonnée verticale d'une certaine proportion, par exemple 1/3 (en d'autres termes abaisser les points en haut jusqu'à la proportion 2/3, et remonter les points en bas jusqu'à la même proportion) : on obtient une ellipse.

 

Exercices

1. Si je prends un carré de superficie 10 m² et que je diminue deux de ses côtés opposés de 1/3, quelle est la superficie du rectangle que j'obtiens ?
2. Si je prend un cercle de superficie 10 m² et que je l'aplatis de 1/3 comme ci-dessus, quelle est la superficie de l'ellipse que j'obtiens ?

Réponses

 

 

Plan général du cours

Contacter le professeur

 

Réponses

1. Environ 6,67 m².
2. Environ 6,67 m² aussi. Pour s'en convaincre, imaginer le cercle initial rempli d'un très grand nombre de minuscules petits carrés. Réduire les côtés verticaux de chacun des minuscules carrés de 1/3, on obtiendra plein de petits rectangles dont l'ensemble forme presque parfaitement une ellipse.