Cours de mathématiques de 5eLes cônes |
|
|
|
|
Video |
|
Texte
On était passé des prismes aux cylindres en prenant pour base un cercle au lieu d'un polygone. Avec la même opération on passe des pyramides aux cônes.
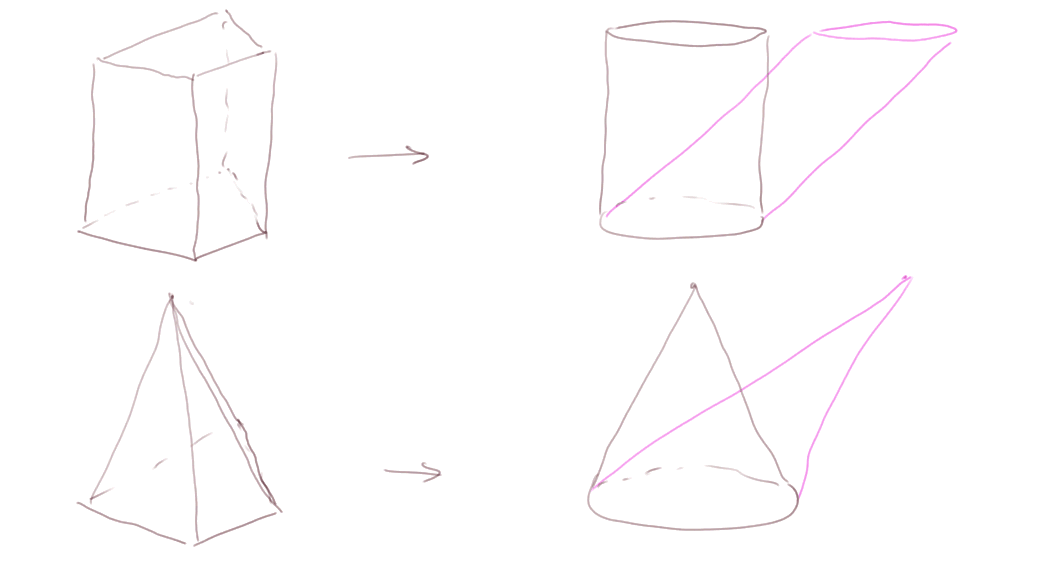
Cela s'applique aussi bien aux cylindres droits ou aux cônes "droits" (dits "de révolution") qu'aux cylindres ou aux cônes penchés.
Le volume d'une pyramide quelconque (avec axe de symétrie vertical ou pas) était
V = S x h /3
C'est la même chose pour un cône (de révolution ou penché)
V = S x h /3
S est la surface du cercle de base, et h est la hauteur (c'est-à-dire la distance entre le sommet et le plan de la base).
On peut aussi calculer la surface de la partie conique d'un cône. La formule est un peu plus compliquée.
Pour la calculer, on utilise des minces triangles isocèles de plus en plus nombreux, sur la surface du cône, ayant pour sommet le sommet du cône et pour base un petit segment interceptant un arc du cercle de la base, avec une hauteur, sur la surface du cône, perpendiculaire à la circonférence du cône. Et on utilise le résultat suivant qu'on démontrera plus tard : si on prend un tel mince triangle, le carré de sa hauteur, le long de la surface du cône, est approximativement égal à R2 + h2, où h est la hauteur du cône et R le rayon de la base.
On trouve alors que S, la surface du pourtour du cône, satisfait la formule S2 = π2R2 x (R2 + h2)
On peut imaginer beaucoup d'autres volumes dans l'espace, avec un sommet comme celui d'un cône, et une base de forme quelconque. On ne recontrerait pas de propriétés géométriques nouvelles intéressantes.
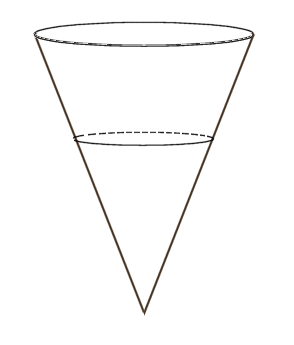
Exercice: Consisérer les deux cônes emboîtés ci-contre.
Le grand a pour hauteur 12 cm, et sa base (en haut) a pour diamètre 7,5 cm.
Le petit emboîté dans le grand a pour hauteur 8 cm.
Montrer que le tronc conique entre les deux a pour volume environ 125 cm3
Problème "d'optimisation" :
-
Je vends des cornets de glace de 250 cm3 sur la plage. (250 cm3 est aussi ce qu'on appelle 25 centilitres ou 25 cl.)

Les cornets sont remplis à ras (mais pas plus) avec de la crème glacée, comme ceux vendus pas les ouvreuses au cinéma. Je voudrais minimiser la surface de biscuit de mes cornets pour qu'ils me coûtent le moins cher possible. Des cônes de quelle hauteur et quel cercle de base dois-je fabriquer ou acheter ? Aide : résoudre le problème en utilisant la formule S2 = π2R2 x (R2 + h2) et en essayant une série de paires R et h, où R et h sont liés par la relation h x πR2 x 1/3 = 250 cm3.
Plan général du cours
Contacter le professeur
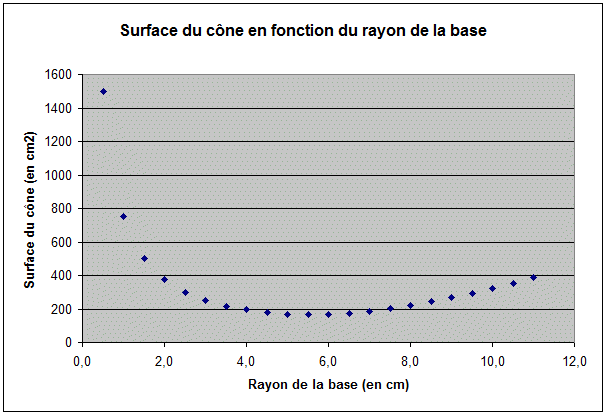
Solution : voici un tableau où on a essayé toute une série de rayons R depuis 10cm jusqu'à 0,5 cm, on a calculé la hauteur nécessaire dans chaque cas pour que V reste 250 cm3, et on a calculé la surface S dans chaque cas aussi.
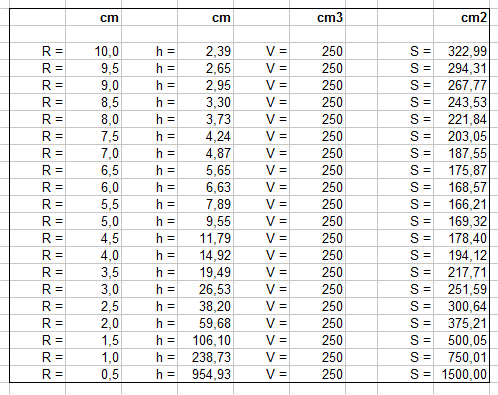
On voit que si R = 10cm, h doit être 2,39 cm et S = 322,99 cm2. A l'inverse si R est très petit, 0,5 cm, le cône doit faire plus de 9 mètres de haut ! Et la surface est alors de 1500 cm2.
La surface de biscuit minimale est obtenue pour R = 5,5 cm, et dans ce cas h = 7,89 cm. C'est un résultat approximatif, car on a essayé seulement de 0,5 cm en 0,5 cm. On pourrait raffiner nos calculs, on trouverait R optimal situé entre 5,52 et 5,53 cm.
Une représentation graphique des résultats est donnée ci-dessous : pour chaque rayon R essayé, on se positionne sur l'axe horizontal à la position correspondant à R, et on met un point à la verticale, à la hauteur correspondant à la surface S pour ce rayon-là. On voit "graphiquement" que la surface minimale est atteinte pour R aux environs de 5,5 cm.
Pour aller plus loin : si vous êtes en Première ou en Terminale, montrez qu'à la surface de biscuit minimale on a h / r = racine carrée de 2.