Cours de mathématiques de 5ePyramides |
|
|
|
|
Video |
|
Texte
Une pyramide est un volume dans l'espace construit de la manière suivante :
- Partir d'un polygone dans le plan
- Choisir un point hors du plan
- Lever tous les segments issus des sommets du polygone jusqu'au point extérieur.
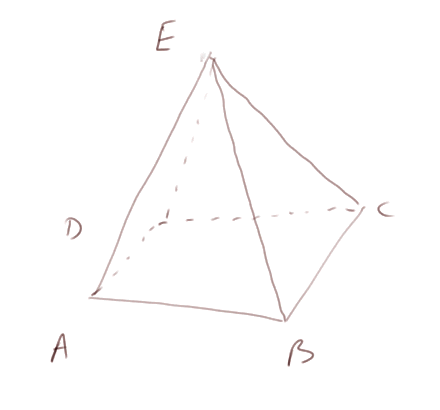
Dans cet exemple, la base est un quadrilatère. On peut prendre pour base n'importe quel polygone convexe. (Un polygone est convexe si quand on prend deux points dans le polygone, tout le segment entre eux l'est aussi.) Par exemple, si on part d'une base triangulaire, on obtient ce qu'on appelle un tétraèdre.
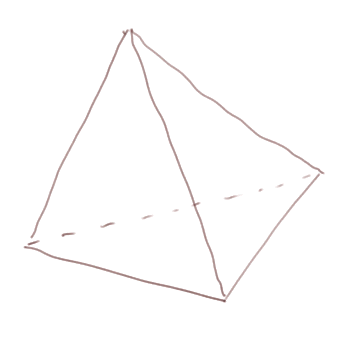
Un tétraèdre a quatre faces. C'est pour cela que ça s'appelle un tétraèdre : "tétra" = 4, "èdre" = côté. Il a aussi six arêtes et quatre sommets.
Un tétraèdre régulier est un tétraèdre dont toutes les faces sont des triangles équilatéraux.
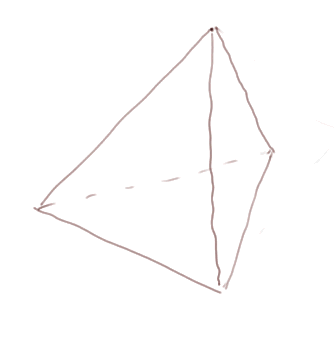
Etant donné notre contrainte de dessin sur une feuille de papier, ou un écran (en tout cas un plan), il faut toujours faire un effort d'imagination.
Les pyramides d'Egypte, à côté du Caire, ont une base carrée et un axe de symétrie vertical.

Dans une leçon de sixième, nous avons reconstitué un cube à l'aide de 3 pyramides identiques. C'étaient des pyramides à base carrée dont l'une des arêtes était perpendiculaire à la base, et de longueur égale au côté de la base.
Nous avons vu que cette pyramide (en rouge ci-dessous) avait pour volume : V = surface de la base x hauteur x 1/3. Mais c'était dans un cas particulier où la surface de la base = a x a, et la hauteur = a.
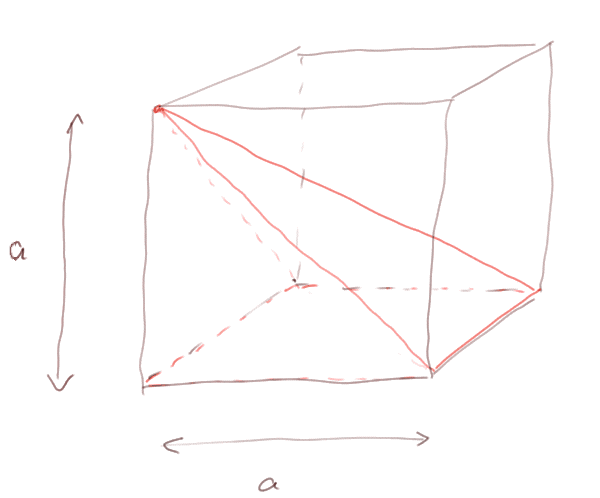
Nous allons voir que cette formule du volume d'une pyramide (base x hauteur x 1/3) est vraie pour toute pyramide, quelque soit la forme de sa base, la position du sommet par rapport à la base, et la hauteur. Il y a plusieurs façons de procéder. Nous allons modifier d'abord la hauteur, ensuite la base.
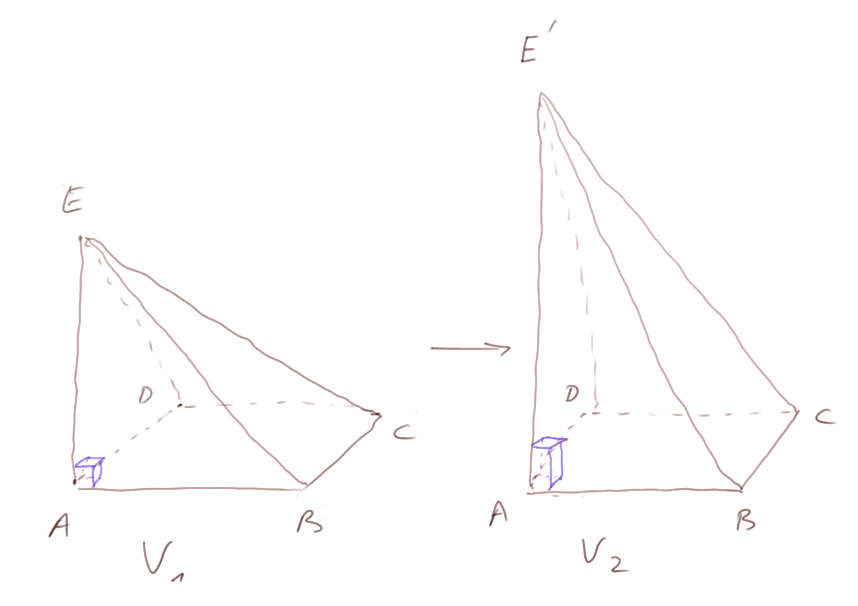
Augmentons la hauteur dans une proportion p (par exemple, p = 1,5). Alors le volume de la nouvelle pyramide est augmenté dans la même proportion
V2 = p x V1
Pourquoi ? Eh bien imaginons la première pyramide remplie d'un très grand nombre N de petits cubes (chacun de volume v). Si j'augmente la hauteur de chaque petit cube dans la proportion p, j'obtiens le même très grand nombre N de petits parallélépipèdes dont le volume de chacun a été multiplié par p, par rapport aux petits cubes. Et ils remplissent la pyramide de droite. Si le volume V1 était égal à N x v, maintenant le volume V2 est égal à N x p x v. Donc on a bien V2 = p x V1. Pour être précis, on fait une petite erreur, mais aussi petite qu'on veut. Donc le volume de la pyramide de droite est p fois celui de celle de gauche.
Maintenant passons de la pyramide de droite (ci-dessus) à une pyramide de même base, et même hauteur, mais où on a déplacé E' vers n'importe quel point F à la même hauteur de la base.
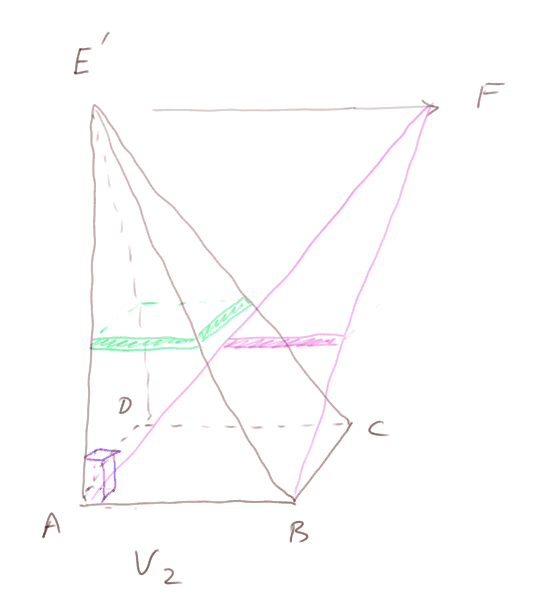
Pour cela on découpe la pyramide en fines tranches horizontales (vertes). On en a tout un empilement de tailles décroissant régulièrement. On peut les faire glisser afin d'obtenir une pyramide dont les faces sont encore planes et qui a pour sommet F. (On utilise pour cela un résultat que nous ne démontrerons formellement qu'en 4e, mais que tout le monde connaît depuis le jardin d'enfant : la bande verte qui découpe le triangle ABE' reste horizontale et de longueur constante si on modifie le triangle AE'B en déplaçant E' vers F, à même distance du plan ABCD, tout en maintenant A et B à leur place.) Les faces presque verticales ne sont plus tout à fait lisses, mais on peut utiliser des tranches aussi fines qu'on veut, et être aussi près qu'on veut de faces lisses. Donc V2 reste inchangé.
Puis on peut modifier la forme de chaque tranche verte pour en faire un triangle ou un autre polygone. On aura un empilement de polygones de surfaces décroissant régulièrement, formant une pyramide avec une base de forme quelconque.
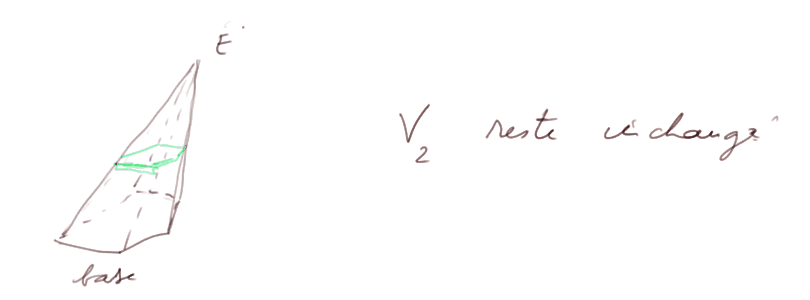
On en conclut que pour n'importe quelle pyramide dont la surface de la base est S et de hauteur h, le volume est
V = S x h x 1/3
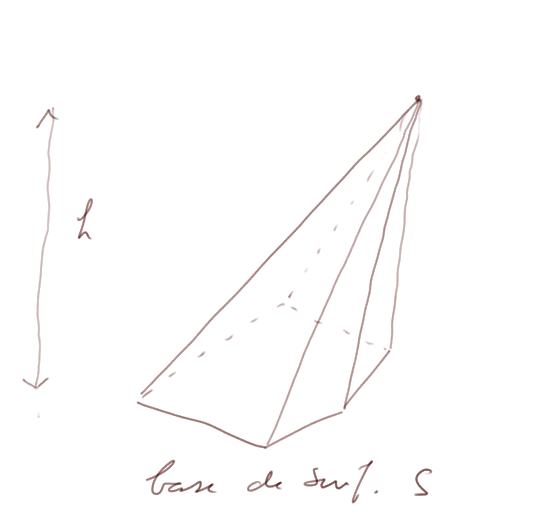
Note : une fois établi le résultat sur l'augmentation de la hauteur qui augmente le volume de la pyramide dans la même proportion, on peut aussi démontrer tout le reste sans faire appel à un découpage en fines tranches, mais en résonnant sur des pyramides de base triangulaire et triangulaire rectangle, comme nous l'avons fait dans la leçon précédente pour les prismes droits.
Exercices
- Découper un cube en six pyramides identiques ayant pour base chaque face du cube et pour sommet le centre du cube.
- Vérifier que chaque pyramide a pour volume 1/6 du volume du cube.
Plan général du cours
Contacter le professeur
Réponses
- Découper un cube en six pyramides identiques ayant pour base chaque face du cube et pour sommet le centre du cube. Réponse :
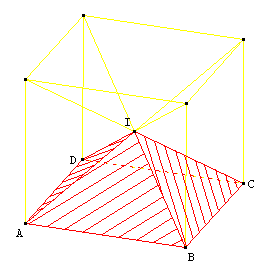
source du dessin : https://www.maths.ac-aix-marseille.fr/debart/index.html
- Vérifier que chaque pyramide a pour volume 1/6 du volume du cube. Réponse : si AB = 1 m, chaque pyramide a pour volume 1m x 1m x (1/2)m x 1/3 = 1/6 m3.