Cours de mathématiques de 5eTriangles : propriétés élémentaires |
|
|
|
|
Video |
|
Texte
Les triangles dans un plan ont un certain nombre de propriétés élémentaires. La première concerne les longueurs : AB + AC est supérieure ou égale à AC.
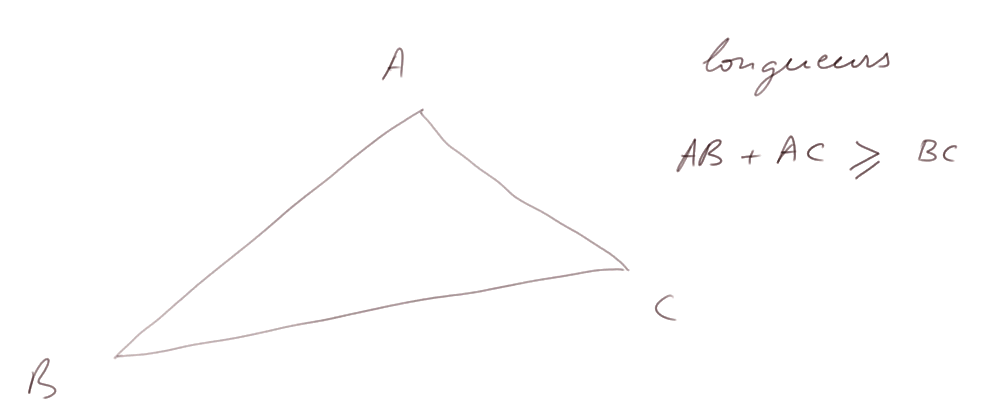
Dans la pratique, les triangles avec lesquels on travaille le plus sont les triangles rectangles, c'est-à-dire les triangles dont l'un des angles fait 90° (écran 3).
Définition de la distance d'un point P à une droite D. C'est la longueur du segment PH où H est sur la droite D et PH est perpendiculaire à D.
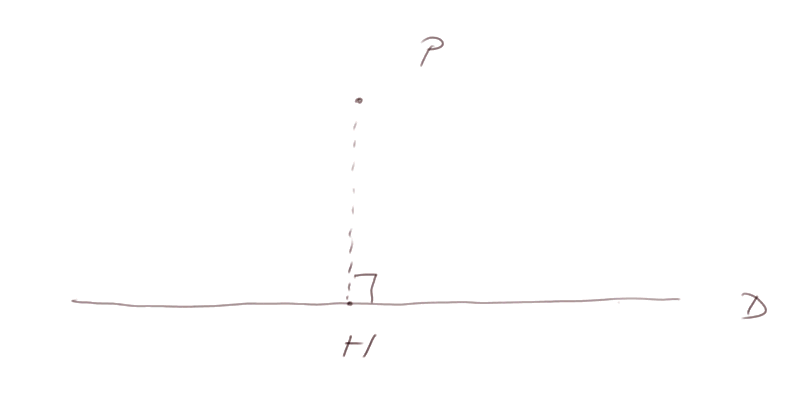
La bissectrice d'un angle est par définition la droite qui partage l'angle en deux angles égaux. Propriété : c'est aussi la droite des points à égale distance des deux côtés de l'angle.
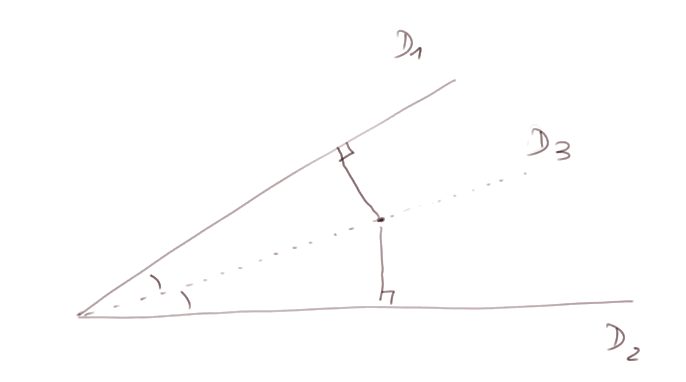
En géométrie élémentaire, la notion de preuve n'a rien d'élémentaire.
La preuve de résultats élémentaires nécessite de remonter à des principes encore plus élémentaires (ou "fondamentaux"). On en acceptera quelques uns sans se soucier de preuve. Puis peu à peu on prouvera des résultats.
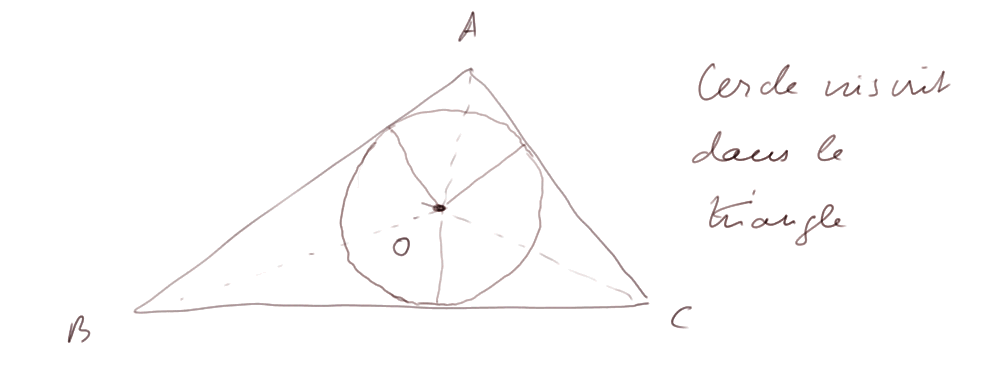
Résultat (qu'on va prouver) : dans un triangle, les 3 bissectrices se coupent en un même point O. En effet considérons la bissectrice de l'angle au sommet B : ses points sont à égale distance de AB et BC. Et considérons la bissectrice de l'angle au sommet A : ses points sont à égale distance de AB et AC. Donc leur intersection O est à égale distance de AC et BC, donc O est aussi sur la bissectrice de l'angle au sommet C.
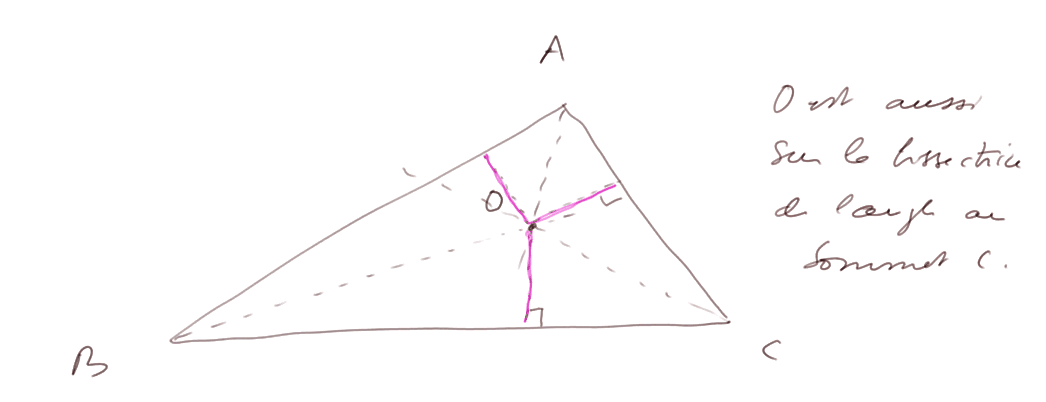
Le point d'intersection des trois bissectrices est le centre d'un cercle touchant chaque côté du triangle en un seul point. C'est le cercle inscrit dans le triangle.
Définition : la médiatrice d'un segment AB est la droite coupant AB en son milieu et perpendiculaire à AB (écran 9).
Propriété : la médiatrice d'un segment AB est aussi l'ensemble des points à égale distance de A et de B.
Les trois médiatrices d'un triangle se coupent en un même point. Preuve : considerer la médiatrice de AB et la médiatrice de BC, elles se coupent en un point P. Ce point P est à égale distance de A et de C, donc il est aussi sur la médiatrice de AC.
Le cercle ayant pour centre l'intersection des médiatrices et passant par A passe aussi par B et par C. C'est le cercle circonscrit au triangle.
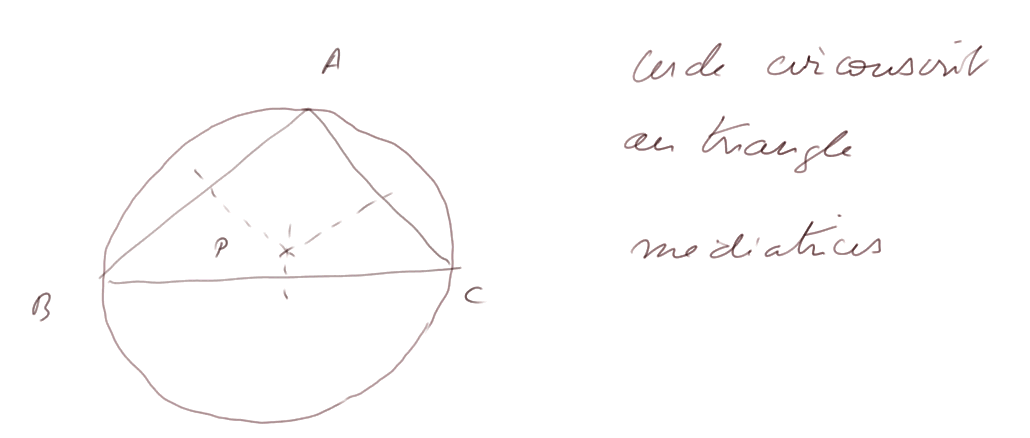
Exercices
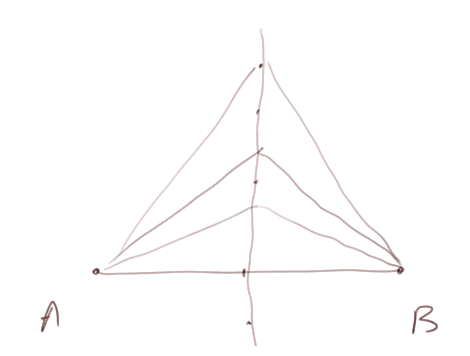
- Avec une feuille de papier, une règle, une équerre et un compas, tracer un triangle rectangle et l'intersection de ses médiatrices. Puis tracer le cercle circonscrit.
- Vérifier que l'intersection des médiatrices est au milieu du grand côté du triangle rectangle (appelé "l'hypoténuse")
*******************************************
Problème
Nous sommes sur un navire, et nous voulons faire un point pour savoir où nous nous trouvons exactement, et le reporter sur une carte. Nous repérons les angles de trois amers par rapport à notre cap (= la direction dans laquelle avance notre navire).
(Définition d'un amer : objet ou bâtiment fixe et visible, situé sur une côte et servant de point de repère pour la navigation. © Larousse.)
Nous commençons par noter sur une carte marine la droite entre notre bateau et l'amer 1. Puis nous prenons l'amer 2, alors que notre bateau a un peu avancé. Au moment du repérage de l'amer 2, le navire est sur la droite verticale qui coupe l'axe horizontal au point (3 ; 0). Enfin nous prenons l'amer 3 quand notre navire est aux environs du point (2 ; 0).
Tracer le triangle formé par les trois droites de répérage.
Quand j'étais marin, la règle à l'Ecole navale était de considérer que le navire était alors au milieu du triangle. Et cela ne souffrait pas de discussion.
Montrer pourtant que c'est faux : dans l'exemple ci-dessus au moment de l'amer 3 le navire est au nord-ouest du triangle.
*******************************************
Plan général du cours
Contacter le professeur
Réponses aux exercices : vous découvrez donc que l'hypoténuse du triangle rectangle est un diamètre du cercle circonscrit.
Réponse au problème : voici la position du navire au moment du repérage de l'amer 3.