Cours de mathématiques de 5eTriangles : propriétés avancées |
|
Video |
Texte
Dans la leçon précédente, nous avons vu des propriétés élémentaires des triangles : les bissectrices se coupent au centre du cercle inscrit, et les médiatrices se coupent au centre du cercle circonscrit. Nous allons maintenant étudier une propriété plus avancée : les 3 médianes se coupent en un même point.
Pour démontrer ce fait, nous partirons d'une propriété plus élémentaire que nous traiterons en "vérité géométrique" qu'il n'est pas nécessaire de démontrer dans notre approche de la géométrie. Elle est d'ailleurs équivalente à une autre "vérité géométrique" : un parallélogramme a un centre de symétrie au point d'intersection de ses diagonales.
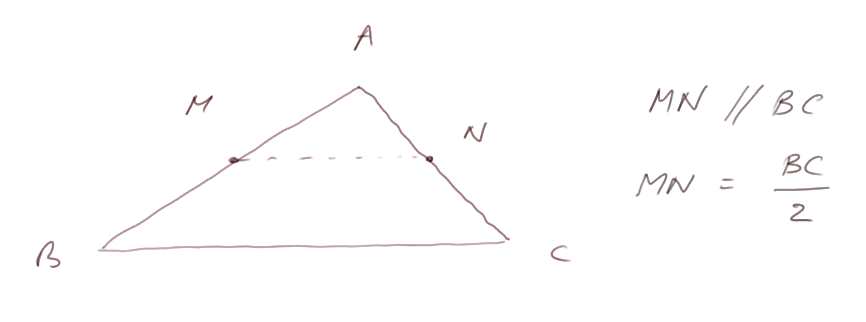
"La droite des milieux" : dans un triangle ABC quelconque, si M est le milieu de AB et N le milieu de AC, alors le segment MN est parallèle au segment BC, et sa longueur est la moitié de celle de BC. Inversement si M est le milieu de AB et qu'on trace passant par M une droite parallèle à BC alors elle coupe AC au milieu de AC, c'est-à-dire au point N.
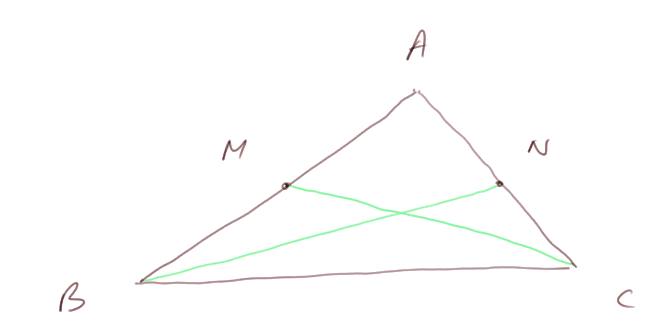
Médianes d'un triangle : la droite BN est appelée médiane issue du B ; et la droite CM est appelée médiane issue de C.
Résultat important : les trois médianes se coupent en un même point.
Pour le démontrer, considérons aussi la troisième médiane et supposons que les trois médianes ne se coupent pas en un point, mais forment un petit triangle. (Et notons les points M', N' et P' ainsi que le montre la figure ci-dessous.)
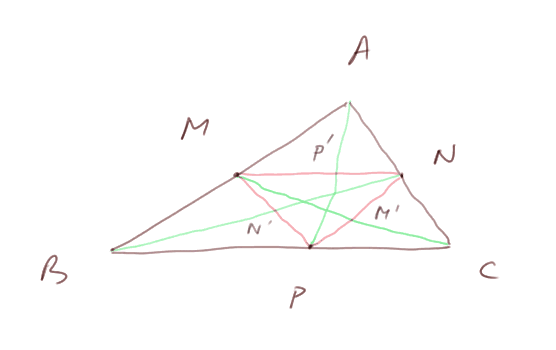
Par la vérité géométrique de "la droite des milieux", on a
MP' est parallèle à BC et de longueur moitié que BP
NM' est parallèle à AB et de longueur moitié que AM
PN' est parallèle à AC et de longueur moitié que CN
Enfin le triangle MNP a tous ses côtés parallèles à ceux de ABC, et il a donc aussi les mêmes angles (utiliser la vérité géométrique sur les angles formés par une sécante à deux parallèles).
Par ailleurs AP est aussi la médiane de MNP issue de P. BN est aussi la médiane de MNP issue de N, et CM est aussi la médiane de MNP issue de M.
Donc MNP est identique à ABC redessiné à l'échelle 1/2, et retourné de 180°.
Alors le petit triangle formé par les grandes médianes doit aussi être identique à lui-même redessiné à l'échelle 1/2.
Ce n'est possible que si ce petit triangle est en réalité un point.
On appelle ce point : G. Il a une propriété physique très importante : si le triangle est découpé dans une plaque d'acier homogène d'épaisseur constante, il tiendra en équilibre sur un pied très fin, pourvu que le point G soit à l'intérieur de la section du pied.
Pour cette raison, on appelle ce point G "le centre de gravité" du triangle.
Tournons-nous maintenant vers les hauteurs d'un triangle. Ce sont les trois segments issus de chaque sommet et perpendiculaires au côté opposé.
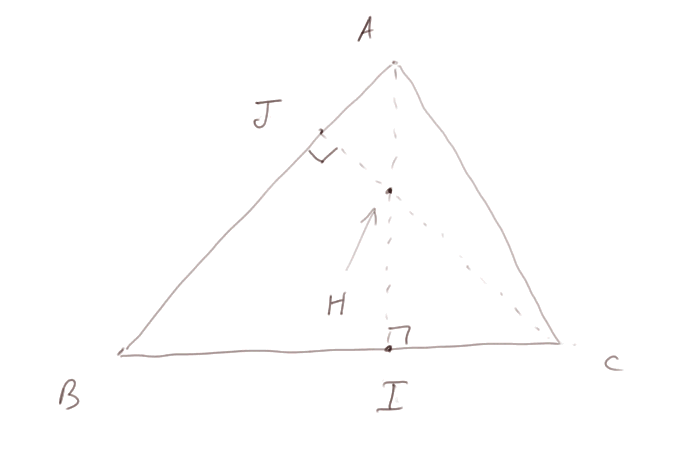
Là encore les trois hauteurs se coupent en un même point. En d'autres termes si H est l'intersection des hauteurs AI et CJ, alors BH est perpendiculaire à AC. (Sur la figure nous ne l'avons pas dessiné. Il couperait AC en un point naturellement appelé K.)
Nous ne démontrerons pas ce résultat, mais il n'est pas difficile à démontrer en raisonnant sur les angles de divers triangles rectangles.
Pour finir, présentons un résultat fort joli et surprenant : dans un triangle quelconque l'intersection P des médiatrices, l'intersection G des médianes, et l'intersection H des hauteurs, sont trois points alignés.
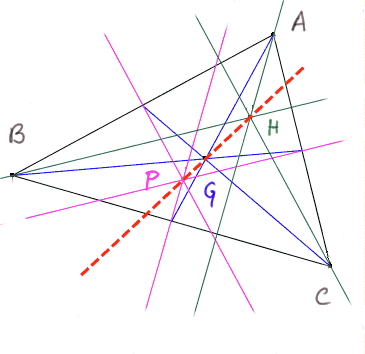
Source du dessin : https://ww3.ac-poitiers.fr/math/prof/logic/geolabo/index.htm
(Démonstration qui peut être omise : on utilise une transformation dans le plan autour du point G (intersection des médianes) : à tout point Q on fait correspondre Q' tel que le segment QQ' contienne le point G, et la longueur GQ' soit la moitié de la longueur GQ. Cette transformation transforme les sommets A, B et C en les milieux des segments opposés, formant ainsi un triangle d'échelle moitié du premier. Et les hauteurs du premier deviennent les hauteurs du deuxième, qui sont aussi les médiatrices du premier.)
Ce résultat est dû au grand mathématicien d'origine suisse, Leonhard Euler (1707 -1783).
Exercices
- Dessiner soigneusement sur une feuille de papier un triangle quelconque. A l'aide d'une règle graduée et d'une équerre dessiner les trois médiatrices et le point P.
- Dessiner de la même manière les médianes, et vérifier qu'elles se coupent en un même point.
- Vérifier, puis prouver que les médianes se coupent chacune au 2/3 de la distance depuis le sommet dont elle est issue jusqu'au côté opposé. (Raisonner sur le grand triangle initial ABC et le triangle MNP formé par les droites des milieux, qui est une copie à l'échelle 1/2 du premier, et qui a les mêmes droites médianes.)