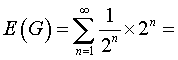
Source : http://www.mazerolle.fr/HPE/Les%20Neoclassiques.htm (un très bon site, que nous recommandons)
1.3 BERNOULLI
: le paradoxe de Saint-Pétersbourg (1738) et l'intuition de l'utilité marginale
Le concept d'utilité marginale allait cependant naître de l'intérêt, déjà
ancien, manifesté par les philosophes au sujet d'un paradoxe connu sous le nom
de "paradoxe de Saint-Pétersbourg", lequel fut résolu par
Daniel BERNOULLI (1700-1782) en 1738, qui lui appliqua sans le nommer le
concept d'utilité marginale décroissante. Le concept d'utilité marginale
décroissante dit simplement ceci : chaque unité supplémentaire de bien que l'on
consomme procure une supplément d'utilité décroissant. Pour voir comment ce
concept s'applique au paradoxe de Saint-Pétersbourg, on rappellera d'abord en
quoi celui-ci consiste. Premièrement, s'il a été appelé ainsi, c'est simplement
parce que
Daniel BERNOULLI (1700-1782) fut pendant quelques années professeur de
mathématiques à Saint-Pétersbourg et que c'est donc logiquement devant
l'académie de Saint-Péterbourg, en 1738, qu'il présenta pour la première fois la
solution à ce paradoxe qui était connu mais sans solution jusqu'alors.
Il s'agit en fait d'un jeu qui consiste à lancer une pièce en l'air et d'observer le résultat. Si la pièce tombe sur face, le joueur gagne 21 ducats et le jeu s'arrête. Si la pièce tombe sur pile, on rejoue. Si la pièce tombe sur face, le joueur gagne 22 ducats = 4 ducats et le jeu s'arrête. Si la pièce tombe sur pile, on rejoue. Le tableau ci-dessous donne les résultats jusqu'à 10 :
| n (nombre de jets) |
Probabilité que face sorte au jet n (mais pas avant) |
Gain du joueur |
| 1 | 1/2 | 2 ducats |
| 2 | 1/2 x 1/2 =1/4 | 22 = 4 ducats |
| 3 | 1/2 x 1/2 x 1/2 =1/8 | 23 = 8 ducats |
| 4 | 1/24 = 1/16 | 24 = 16 ducats |
| 5 | 1/32 | 32 ducats |
| 6 | 1/64 | 64 ducats |
| 7 | 1/128 | 128 ducats |
| 8 | 1/256 | 256 ducats |
| 9 | 1/512 | 512 ducats |
| 10 | 1/1024 | 1024 ducats |
Source du tableau : http://plato.stanford.edu/entries/paradox-stpetersburg/
La question qui se posait, était de savoir quelle somme un joueur est disposé à payer pour jouer à ce jeu. On pensait que la réponse rationnelle était donnée par l'espérance mathématique du gain, mais cette solution ne fonctionne pas, car l'espérance de gain est infinie (voir ci-après). Or personne n'est prêt à donner une somme infinie pour jouer à ce jeu (4 ducats est semble-t-il un maximum, et encore ....).
L'espérance de gain, E(G), se calcule ainsi :
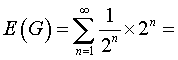
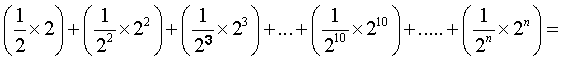
![]()
La solution proposée par Daniel BERNOULLI (1700-1782) consiste à dire que ce qui compte, ce n'est pas l'espérance du gain, mais l'espérance de l'utilité du gain est positive mais croît à un taux décroissant. C'est-à-dire par exemple que l'utilité que me procure 2 millions de ducats n'est pas le double de l'utilité que me procure 1 million de ducats, mais moins.
Daniel BERNOULLI (1700-1782) propose alors de mesurer l'utilité du gain par le logarithme (en base 10) du gain. C'est-à-dire que :
![]()
L'espérance de l'utilité du gain, E(G), se calcule ainsi :
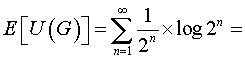
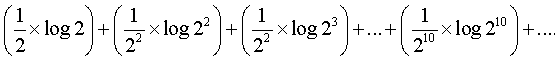 |
Le tableau ci-dessous donne les résultats jusqu'à 15 (puis 24) :
| n (nombre de jets) |
Probabilité que face sorte au jet n (mais pas avant) |
Gain du joueur |
Proba de gain multipliée par Log[gain] |
|
| 1 | 1/2 | 2 ducats | (1/2) Log[2]=0,1505 | 0,1505 |
| 2 | 1/2 x 1/2 =1/4 | 22 = 4 ducats | (1/4) Log[4]=0,1505 | 0,3010 |
| 3 | 1/2 x 1/2 x 1/2 =1/8 | 23 = 8 ducats | (1/8) Log[8]=0,1128 | 0,4138 |
| 4 | 1/24 = 1/16 | 24 = 16 ducats | (1/16) Log[16]=0,0752 | 0,4890 |
| 5 | 1/32 | 32 ducats | (1/32) Log[32]=0,0470 | 0,5360 |
| 6 | 1/64 | 64 ducats | (1/64) Log[64]=0,0282 | 0,5642 |
| 7 | 1/128 | 128 ducats | (1/128) Log[128]=0,0164 | 0,5806 |
| 8 | 1/256 | 256 ducats | (1/256) Log[256]=0,0094 | 0,59 |
| 9 | 1/512 | 512 ducats | (1/512) Log[512]=0,0052 | 0,5952 |
| 10 | 1/1024 | 1024 ducats | (1/1024) Log[1024]=0,0029 | 0,5981 |
| 11 | 1/2048 | 2048 ducats | (1/2048) Log[2048]=0,0016 | 0,5997 |
| 12 | 1/4096 | 4096 ducats | (1/4096) Log[4096]=0,0009 | 0,6006 |
| 13 | 1/8192 | 8192 ducats | (1/8192) Log[8192]=0,0004 | 0,6010 |
| 14 | 1/16384 | 16384 ducats | (1/16384) Log[16384]=0,0002 | 0,6012 |
| 15 | 1/32768 | 32768 ducats | (1/32768) Log[32768]=0,0001 | 0,6013 |
| 24 | 0,60206 |
Source du tableau : http://plato.stanford.edu/entries/paradox-stpetersburg/
Le graphique ci-dessous permet de visualiser l'espérance de l'utilité du gain sous forme d'une surface. Cette espérance est égale à 0,60206. Or, puisque U=log(G), on a 0,60206=log(G), soit G = 4 ducats. Autrement dit, un joueur rationnel est prêt à investir 4 ducats pour participer au jeu et non pas un nombre infini de ducats, comme le laissait penser le résultat obtenu simplement en prenant l'espérance du gain.
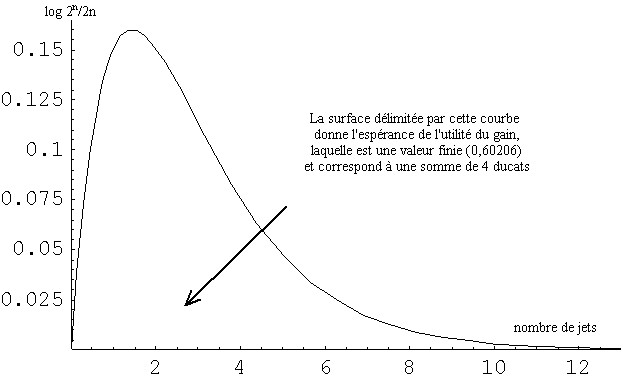
La résolution du paradoxe a été obtenue par Daniel BERNOULLI (1700-1782) en utilisant la fonction log(U) dont la caractéristique est de croître à un taux décroissant. Les néoclassiques reprirent cette idée que chaque accroissement d'utilité est inférieur au précédent : c'est l'utilité marginale.