HISTOIRE DE LA PHILOSOPHIE OCCIDENTALE, par Bertrand Russell, © 1945
---------------------------------------------------------------------------------------
publicité
---------------------------------------------------------------------------------------
I.1.3 : PYTHAGORE
Pythagore (c. 580 - c. 495), dont l'influence dans l'Antiquité et à l'époque moderne est le sujet de ce chapitre, est intellectuellement l'un des hommes les plus importants qui aient jamais vécu, aussi bien quand il était sage que quand il était déraisonnable. Les mathématiques, au sens de démonstrations déductives indiscutables, commencent avec lui. Il est aussi intimement lié à une forme particulière de mysticisme. L'influence des mathématiques sur la philosophie, en partie à cause de lui, a été, depuis son époque, à la fois profonde et regrettable.
Samos
Commençons par le peu que nous sachions sur sa biographie. Il est né sur l'île de Samos près de la côte ionienne [non loin de Milet], et il était dans la force de l'âge vers -532. Certains disent qu'il était le fils d'un citoyen important nommé Mnésarchos, d'autres qu'il était le fils du dieu Apollon ; je laisse au lecteur le soin de choisir entre ces deux possibilités. A son époque Samos était dirigée par le tyran Polycrate, un vieux ruffian devenu immensément riche, et qui avait une vaste flotte de navires
Samos était la rivale commerciale de Milet ; ses marchands allaient loin au Moyen-Orient et dans toute la Méditerranée, par exemple jusqu'à Tartessos en Espagne, qui était célèbre pour ses mines [origine de l'entreprise Rio Tinto].
Polycrate devint tyran de Samos aux environs de -535, et régna jusqu'en -515. Il n'était pas encombré par trop de scrupules moraux ; il élimina ses deux frères, qui étaient au départ associés avec lui dans la tyrannie, et il utilisa sa vaste flotte pour la piraterie. Il profita du fait que Milet s'était récemment soumise à la Perse [on est avant la rébellion ionienne écrasée par Darius, qui marque le début des guerres médiques]. Afin de contrer toute expansion des Perses vers l'ouest, il s'allia à Amasis, roi d'Egypte. [R. utilise constamment le mot roi là où on utilise plus communément le mot pharaon, mais il est vrai que ce dernier terme semble conférer une sorte d'autorité encore supérieure par rapport aux monarques ordinaires, ce qui ne correspond pas à la réalité -- pratiquement tous les monarques se réclament d'une ascendance divine, avec un contact particulier avec les dieux.] Mais quand Cambyse, roi de Perse, consacra toute son énergie à la conquête de l'Egypte, Polycrate se rendit compte qu'il avait des chances de gagner, et changea de côté. Il envoya une flotte, composée de ses ennemis politiques, attaquer l'Egypte ; mais les équipages se mutinèrent et se tournèrent contre Samos pour l'attaquer. Polycrate eut toutefois le dessus, mais il finit par tomber à cause d'un appel traître à son avarice. Le satrape perse de Sardes [qui avait remplacé Crésus] fit part de son intention de se rebeller contre le Grand Roi de Perse, et qu'il était prêt à verser de vastes sommes pour l'aide de Polycrate. Celui se rendit sur la côte pour une entrevue, fut capturé et crucifié.
Polycrate [qui n'avait pas que des défauts] était un patron des arts, et il embellit Samos avec des édifices publics remarquables. Anacréon (-550, -464) fut son poète de cour officiel. Pythagore cependant n'aimait pas le gouvernement de Polycrate, et quitta l'île de Samos. On dit -- et ce n'est pas impossible -- que Pythagore séjourna en Egypte, et que c'est là qu'il aurait appris une grande partie de sagesse. Quoi qu'il en soit, il finit par s'établir à Crotone, en Italie du Sud.
Crotone
Les villes grecques du sud de l'Italie, de même que Samos ou Milet, étaient riches et prospères ; en outre, elles n'étaient pas exposées à la menace des Perses. Les deux plus grandes étaient Sybaris et Crotone. Sybaris est restée proverbiale pour son luxe ; sa population, à l'époque de son plus grand éclat, était estimée par Diodore de Sicile (historien grec du premier siècle avant Jésus-Christ) à 300 000 habitants, même s'il ne fait aucun doute que ce chiffre soit exagéré. Crotone avait à peu près la même taille que Sybaris. L'activité économique de chacune des deux villes consistait en l'importation de produits d'Ionie en Italie, en partie pour la consommation, en partie pour réexport vers la Gaule et l'Espagne. Les différentes cités grecques du sud de l'Italie (appelée aussi Grande-Grèce) se combattaient farouchement entre elles ; quand Pythagore arriva à Crotone, elle venait juste d'être défaite par Locri (encore appelée Locres). Peu après son arrivée, cependant, Crotone remporta la victoire dans sa guerre contre Sybaris, qui fut totalement détruite (-510). Sybaris avait été en relation étroite avec Milet. Crotone était célèbre pour ses connaissances en médecine ; un certain Démocédès de Crotone devint le médecin de Polycrate puis de Darius.
À Crotone Pythagore fonda une société de disciples, qui pendant un temps eut une influence sur la ville. À la fin les citoyens se soulevèrent contre lui, et il partit à Métaponte (aussi en Grande-Grèce), où il mourut. Il devint rapidement une figure mythique, à qui l'on attribuait des miracles et des pouvoirs magiques. Il avait aussi fondé une école de mathématiques. Ainsi deux traditions opposées se disputent sa mémoire, et la vérité est difficile à démêler du mythe.
Pythagore est l'un des hommes les plus intéressants et déroutants dans toute l'histoire. Non seulement les récits le concernant mélangent inextricablement vérités et mythes, mais même dans leurs aspects les plus dépouillés et les moins douteux ils nous présentent une psychologie très singulière. Il peut être décrit, en résumé, comme une combinaison d'Einstein et de Mary Baker Eddy (1821-1910, Américaine fondatrice du mouvement de la Science Chrétienne). Il fonda une religion, dont les principaux aspects sont la transmigration des âmes et le grave péché que constitue la consommation de fèves. Sa religion fut organisée avec un clergé, qui, ici ou là, prit le contrôle de l'Etat et établit l'autorité des saints. Mais les mécréants avaient envie de manger des fèves, et tôt ou tard ils se rebellèrent. Quelques-unes des règles de l'ordre pythagoricien sont listées ci-dessous :
1. S'abstenir de manger des fèves.
2. Ne pas ramasser ce qui est tombé par terre.
3. Ne pas toucher un coq blanc.
4. Ne pas briser le pain.
5. Ne pas enjamber une séparation transversale.
6. Ne pas remuer le feu avec un tisonnier en fer.
7. Ne pas manger du pain en mordant dans une miche entière.
8. Ne pas retirer des éléments à une guirlande.
9. Ne pas s'asseoir sur une mesure d'un quart.
10. Ne pas manger le coeur.
11. Ne pas marcher le long des grand-routes.
12. Ne pas laisser les hirondelles partager son toit.
13. Quand un pot est retiré du feu, ne pas laisser sa marque dans les cendres, mais les secouer pour les effacer les traces.
14. Ne pas regarder dans un miroir à côté d'une lumière.
15. Quand vous vous levez de votre lit, rouler les draps ensemble et effacer les traces de votre corps.
Tous ces préceptes sont de même nature que les tabous primitifs [et évoquent des Troubles Obsessionnels Compulsifs].
Pythagore est avant tout un mystique
Francis Cornford (1874-1943), dans son livre "From Religion to Philosophy: A Study in the Origins of Western Speculation" publié en 1912, dit qu'à son avis "l'école de Pythagore représente le principal courant de cette tradition mystique que nous opposons d'une manière générale à la tendance scientifique". Il regarde Parménide, qu'il appelle "le découvreur de la logique", comme "un rejeton du pythagorisme". Et il dit que "Platon lui-même, tel qu'on le retrouve dans la philosophie italienne, y puise l'essentiel de son inspiration".
Le Pythagorisme, dit encore Cornford, était un mouvement de réforme de l'Orphisme ; et l'Orphisme était un mouvement de réforme du culte de Dionysos.
L'opposition entre le rationnel et le mystique, qui traverse toute l'histoire jusqu'à nos jours, apparut d'abord chez les Grecs comme une opposition entre les dieux de l'Olympe et ces autres dieux moins civilisés qui ont davantage d'affinités avec les croyances primitives qu'étudient les anthropologues.
Dans cette division, Pythagore était largement du côté du mysticisme, bien que son mysticisme fût d'une sorte particulière très intellectualisée. Il s'attribuait à lui-même un caractère semi-divin, et il semble qu'il ait déclaré : "Il y a les hommes et les dieux, et il y a les êtres comme Pythagore." Tous les systèmes qu'il a inspirés, poursuit Cornford, "sont tournés vers l'autre monde [appelé aussi "l'au-delà"], accordant plus de valeur à l'unité invisible de Dieu, qu'au monde visible, condamné comme étant faux et une illusion, un milieu turbide dans lequel les rais de lumière céleste sont troublés et estompés par la brume et l'obscurité."
Dicéarque (c.-347, c.-285, disciple d'Aristote) dit que Pythagore a enseigné "d'abord, que l'âme est une chose immortelle, et qu'elle se transforme en d'autres êtres vivants ; ensuite, que quoi que ce soit qui existe [exista avant sous une autre forme et] renaîtra dans un certain cycle, rien n'étant absolument nouveau ; et que toutes les choses qui sont nées avec de la vie en elles doivent être traitées comme pareilles à nous". On dit que Pythagore, tel Saint François d'Assise 17 siècles plus tard, prêchait aux animaux.
Dans la société qu'il fonda, les hommes et les femmes étaient acceptées sur un pied d'égalité ; la propriété était détenue en commun, et un mode de vie commun était adopté. Même les découvertes scientifiques et mathématiques étaient considérées comme collectives, et, dans un sens mystique, encore dues à Pythagore même après sa mort. Hippase de Métaponte, qui viola cette règle, fit naufrage et cela fut attribué à la colère des dieux pour son impiété.
Mais qu'est-ce que tout cela a à voir avec les mathématiques ?
Les mathématiques sont l'enfant de la contemplation mystique
C'était lié par une éthique qui exaltait la vie contemplative. Burnet résume cette éthique ainsi :
"Nous sommes des étrangers en ce monde ; le corps est la tombe de l'âme ; et cependant nous ne devons pas chercher à nous échapper en commettant un meurtre sur nous-même ; car nous sommes le troupeau de Dieu qui est notre berger, et sans son ordre nous n'avons pas le droit de nous échapper. Dans cette vie, il y a trois sortes d'hommes, de même qu'il y a trois sortes de gens qui viennent aux Jeux Olympiques. La classe la plus basse consiste en les gens qui viennent pour vendre et acheter, la suivante plus élevée est formée de ceux qui participent aux épreuves. Tout en haut, cependant, se trouve ceux qui viennent simplement en spectateurs. La plus grande purification de toutes est, par conséquent, la science désintéressée, et c'est l'homme qui se consacre à elle, l'authentique philosophe, qui s'est le plus effectivement libéré de la 'roue de la naissance'."
Les changements dans le sens des mots sont souvent très instructifs. J'ai parlé précédemment de l'évolution du mot "orgie" ; maintenant je voudrais parler de celle du mot "théorie". C'était au départ un mot orphique, que Cornford interprète comme "contemplation admirative et passionnée". Dans cet état, explique-t-il, "le spectateur est identifié avec le Dieu souffrant, il meurt dans sa mort, et s'élève à nouveau dans sa nouvelle naissance". Pour Pythagore, la "contemplation admirative et passionnée" était intellectuelle, et provenait de la connaissance mathématique. De cette façon, via le pythagorisme, le mot "théorie" en est graduellement venu à prendre son sens moderne ; mais pour tous ceux qui étaient inspirés par Pythagore il conserva un élément de révélation extatique. Pour ceux qui ont appris à contre-coeur un peu de mathématiques à l'école cela peut paraître étrange ; mais pour ceux qui ont fait l'expérience du plaisir enivrant de la soudaine compréhension d'un résultat apporté par les mathématiques, de temps en temps, s'ils aiment ça, le point de vue pythagoricien semblera complètement naturel même s'il n'est pas vrai. Il peut sembler que le philosophe empirique soit l'esclave de son matériau, mais que le pur mathématicien, comme le musicien, est un libre créateur de son monde de beauté ordonnée.
Il est intéressant d'observer, dans la description que donne Burnet de l'éthique pythagoricienne, la différence avec les valeurs modernes. Dans le cas d'un match de football, les esprits modernes jugent que les joueurs sont plus éminents que les spectateurs. De même en ce qui concerne l'Etat : ils admirent davantage les candidats à une élection que les simples électeurs. Ce changement de système de valeurs est lié au changement dans le système social -- le guerrier, le gentleman, le ploutocrate et le dictateur, chacun a ses propres standards sur ce qui est bien et vrai. Le gentleman est habitué depuis longtemps à la théorie philosophique, parce qu'elle est associée au génie grec, que la vertu de la contemplation a reçu l'approbation théologique, et parce que l'idéal de la vérité désintéressée est l'honneur de la vie académique. Le gentleman dont il s'agit vit dans une société d'égaux, qui eux-mêmes vivent du travail d'esclaves, ou du moins de gens dont le statut social inférieur n'est pas discuté. Il convient d'observer que cette définition inclut le saint et le sage, dans la mesure où ils mènent une vie contemplative plutôt qu'active.
Les définitions modernes de la vérité, comme celles du pragmatisme et de l'instrumentalisme, qui sont plus pratiques que contemplatives, sont inspirées par l'industrialisme par opposition à l'aristocratie.
Quoi qu'on pense d'un système social qui tolère l'esclavage, c'est au gentleman, dans le sens ci-dessus, que nous devons les pures mathématiques. L'idéal contemplatif, puisque il a conduit à la création des pures mathématiques, a été la source d'une activité utile ; cela a accru le prestige de la vie contemplative, et l'a valorisée en théologie, en éthique et en philosophie, d'une manière qu'elle n'aurait sinon pas eue.
[Evidemment il s'agit là des toutes premières mathématiques grecques, il y a 25 siècles. Elles pouvaient être la "conséquence d'une attitude contemplative". Pour nous aujourd'hui la "vie contemplative" est plutôt associée à l'inactivité dans un état perpétuel de rêve mystique. Et les mathématiques qui pouvaient être encore une activité de dilettante jusqu'à Fermat (c. 1600 - 1665), ou même Newton, Leibniz et le début du XVIIIe siècle, sont aujourd'hui un métier exigeant beaucoup de travail.]
Nous en avons suffisamment dit sur l'explication des deux aspects de Pythagore : comme prophète religieux et comme pure mathématicien. Dans ces deux branches il a eu une influence immense, et les deux n'étaient pas aussi séparées qu'ils n'apparaissent à un esprit moderne.
La plupart des sciences, à leur début, ont été liées à une forme de croyance, qui leur donna une valeur fictive. L'astronomie était liée à l'astrologie, la chimie à l'alchimie. Les mathématiques étaient liées à une forme plus subtile d'erreur. La connaissance mathématique semblait certaine, exacte, et applicable au monde réel ; en outre leurs savoirs étaient atteints par la pure pensée, sans avoir besoin d'observer. Par conséquent, on pensait qu'elles étaient un idéal, qui restait inaccessible à la connaissance empirique du quotidien. On pensait, sur la base des mathématiques, que la pensée était supérieure aux sens, à l'intuition et à l'observation. Si le monde des sens, qu'on peut aussi appeler le monde concret, matériel, ne collait pas avec les mathématiques, tant pis pour le monde concret. De diverses manières on chercha des méthodes pour s'approcher de l'idéal du mathématicien, et les suggestions qui en résultèrent furent la source de beaucoup d'erreurs en métaphysique et en théorie de la connaissance. Cette forme de philosophie [singeant les mathématiques] commença avec Pythagore.
"Tout est nombre"
Pythagore, comme chacun sait, a dit que "toute chose est nombre". Cette affirmation, interprétée par un esprit moderne, est dénuée de sens, mais ce qu'il voulait dire n'était pas tout à fait dénué de sens. Il découvrit l'importance des nombres en musique, et le lien qu'il établit entre musique et arithmétique survit encore dans les termes mathématiques "moyenne harmonique" [la moyenne harmonique des deux nombres positifs a et b est 2ab/(a+b), tandis que leur moyenne arithmétique est (a+b)/2 et leur moyenne géométrique est la racine carrée de ab] ou "série harmonique" [1 + 1/2 + 1/3 + 1/4 + 1/5 + etc.].
[Du côté des mathématiques : d'une manière générale, pour n nombres positifs a, b, c.... f, leur moyenne harmonique est l'inverse de la moyenne arithmétique de leurs inverses. Ecrit avec une formule, c'est n / (1/a + 1/b + 1/c + ... + 1/f).
Du côté de la musique : si on prend par exemple un do de fréquence 261,63 Hertz, sa première harmonique (dite encore "harmonique de rang 1") est, par définition, elle-même ; sa deuxième harmonique est l'octave au dessus (c'est-à-dire la note de fréquence 523,26 = 2 x 261,63), sa troisième harmonique est obtenue en multipliant 261,63 par 3 (= 784,89 Hz). Et cette note, qui est un sol, est aussi l'octave au-dessus (ou deuxième harmonique) du sol de fréquence 392,45 Hz.]
Il pensait aux nombres comme à des formes, tels qu'ils apparaissent par exemple sur des dés ou des cartes à jouer. Nous parlons toujours de carrés ou de cubes de nombres, qui sont des termes qu'on lui doit. Il parlait aussi de nombres oblongues, triangulaires, pyramidaux, et ainsi de suite. C'étaient les nombres de cailloux [préférablement eux-mêmes bien sphériques comme des oranges dans un cageot] nécessaires pour faire les formes en question. Il pensait vraisemblablement au monde comme fait de particules élémentaires [mais pas encore comme y pensait Démocrite], et aux corps comme construits à la manière des molécules avec des atomes arrangés en différentes formes. De cette façon, il espérait faire de l'arithmétique l'outil fondamental pour l'étude de la physique et de l'esthétique.
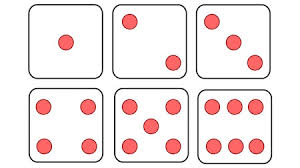
Faces d'un dé : les nombres sont représentés par des figures ou formes.
La plus grande découverte de Pythagore, ou de ses disciples immédiats, est la fameuse proposition sur les triangles rectangles, qui dit que la somme des carrés des longueurs des côtés adjacents à l'angle droit est égale au carré de la longueur de l'hypoténuse. Les Egyptiens savaient depuis longtemps qu'un triangle de côtés 3, 4 et 5 avait un angle droit [c'est-à-dire une moitié d'angle plat], mais c'est apparemment les Grecs qui observèrent les premiers que 3² + 4² = 5², et à partir de cette observation parvinrent au résultat général. [En fait, les Egyptiens, et sans doute les Babyloniens, connaissaient de nombreux triplets tels que a² + b² = c², mais ils ne semblent pas en avoir tiré de règles générales en particulier géométriques.]
Malheureusement pour Pythagore, son théorème conduisit immédiatement à la découverte des "incommensurables" (c'est-à-dire les nombres qui ne sont pas fraction de nombres entiers, appelés maintenant les "irrationnels"). Et ceux-ci semblaient infirmer toute sa philosophie sur les nombres !
Dans un triangle rectangle isocèle, le carré de l'hypoténuse est le double du carré d'un côté. Supposons que chaque côté adjacent à l'angle droit mesure un pouce ; quelle est alors la longueur de l'hypoténuse ? Est-ce facilement exprimable en pouces ? Supposons, par hypothèse, que ce soit une longueur de m/n pouces. Alors on a m²/n² = 2. Si m et n ont un facteur commun, divisez m et n pour qu'ils n'en aient plus. Alors soit m soit n doit être impair (car sinon divisez par 2). Cependant on sait que m² = 2n², donc m² est pair, et donc m aussi ; donc forcément n est impair. Mais continuons nos déductions logiques. Puisque m est pair, écrivons-le sous la forme m = 2p. Alors 4p² = 2n², donc n² = 2p². Ce n'est possible que si n est pair lui aussi. C'est une contraction ! Donc notre hypothèse de départ ne peut pas être vraie. Nous avons prouvé par l'absurde qu'aucune fraction m/n ne peut mesurer l'hypoténuse si le côté est 1. La démonstration que nous venons de donner est en substance celle donnée par Euclide dans son livre X.
[Note : On vient donc de voir que les idées de Pythagore sur les nombres furent infirmées par la découverte des incommensurables, par son école-même. De manière comparable, au début du XXe siècle, B. Russell s'attaqua avec A. N. Whitehead, dans leur ouvrage "Principia Mathematica", au projet de démontrer toutes les mathématiques. C'est-à-dire
- d'établir que tous les axiomes employés forment la base d'une théorie qui ne conduit à aucune contradiction et,
- d'établir, en théorie pour toute propostion mathématique, si elle est vraie ou fausse.
Or en 1931 Kurt Gödel démontra dans un court article que le projet de Russell (qui était déjà un objectif de Hilbert) était impossible. Russell a dû se sentir proche de Pythagore...]
Cette démonstration, par l'école de Pythagore de l'incommensurabilité de la diagonale du carré de côté un, montre que, quelle que soit l'unité de longueur choisie, il existe des longueurs qui ne sont pas exprimables comme une fraction (éventuellement supérieure à un) de l'unité choisie. Cela convainquit les mathématiciens grecs que la géométrie devait être étudiée indépendamment de l'arithmétique. Il y a des passages dans les dialogues de Platon qui montrent que le traitement de la géométrie indépendamment de l'arithmétique était déjà bien avancé à son époque ; c'est encore amélioré jusqu'à la perfection chez Euclide.
Des nombres à la géométrie (pour éviter d'utiliser les affreux "incommensurables)
Euclide, dans son Livre II, démontre géométriquement de nombreux résultats qu'on démontre plus naturellement par l'algèbre, comme par exemple (a+b)² = a² + 2ab + b². C'était à cause de la difficulté présentée par les "incommensurables" qu'Euclide préféra les démonstrations géométriques. C'est vrai aussi de son traitement des proportions dans les Livres V et VI. Tout son système est un enchantement logique, et anticipe la rigueur des mathématiciens du XIXe siècle [en particulier l'axiomatisation de la géométrie par Hilbert]. Tant qu'aucune théorie adéquate des incommensurables n'était développée, la méthode d'Euclide passant par la géométrie était la plus satisfaisante. Quand Descartes introduisit la géométrie avec des coordonnées, faisant à nouveau de l'arithmétique la science suprême, il fit l'hypothèse que les incommensurables ne posaient pas de problème, bien qu'à son époque ces nombres, dits irrationnels, fussent encore mystérieux.
[Il faudra attendre des gens comme Dedekind pour en donner des définitions impeccables, ou auparavant les définitions fondées sur des suites et séries.
J'avais appris de l'un de mes profs de prépa les "coupures de Dedekind" et d'autres trucs comme ça. Mais je ne voyais pas ce que ça apportait à la compréhension des irrationnels, car j'en avais une compréhension géométrique naturelle. D'une manière générale, la présentation de l'axiomatique par des profs de maths doctes et médiocres apporte plus de confusion que de clarté. C'est dans le livre de Jacques Dixmier, d'une simplicité et d'une beauté cristalline, sur les nombres réels que j'ai réellement apprécié la beauté et l'utilité de cette structure algébrique.
Il faut noter aussi qu'au XVIe siècle, donc avant Descartes, les mathématiciens italiens avaient aussi introduit d'autres artifices, qui devinrent les nombres complexes. En d'autres termes, les mathématiques post-Renaissance commençaient à être très créatives, et ne s'embarrassaient pas trop de questions fondamentales, tellement elles trouvaient de nouveaux résultats très intéressants, et même utiles pour l'astronomie puis la technologie.]
L'influence de la géométrie sur la philosophie et la méthode scientifique a été profonde. La géométrie, telle qu'établie par les Grecs, commence avec des axiomes qui sont (ou sont considérés comme) self-évidents ; elle poursuit, par raisonnements déductifs, pour parvenir à des théorèmes qui sont loin d'être self-évidents. Ces axiomes et théorèmes sont tenus pour vrais dans notre monde réel, qui est quelque chose donné par l'expérience. Ainsi il apparut possible de découvrir des choses sur notre monde réel en observant d'abord ce qui est self-évident et ensuite en utilisant la déduction -- c'est-à-dire de la pure réflexion.
Cette vue a influencé Platon et Kant, et la plupart des philosophes entre les deux. Quand la Déclaration d'Indépendance des Etats-Unis commence par "Nous tenons ces vérités pour évidentes en elles-mêmes...", elle applique le modèle d'Euclide. La doctrine du XVIIIe siècle sur les droits naturels est la recherche d'une construction axiomatique de la politique. Le format des Principia de Newton, malgré leur présentation qui se veut empirique, est entièrement dominé par Euclide. La théologie, dans sa forme rigoureuse des scolastiques, s'inspire dans son style de la même source.
La religion personnelle est dérivée de l'extase, la théologie des mathématiques ; les deux nous viennent de Pythagore.
Les mathématiques sont, à mon sens, la principale source de croyance en la vérité éternelle et exacte, aussi bien qu'en un monde supersensible et intelligible. La géométrie s'occupe de cercles exacts, mais aucun objet sensible n'est exactement circulaire ; aussi précisément qu'on utilise nos compas, il y aura des imperfections et des irrégularités. Cela suggère le point de vue selon lequel les raisonnements exacts s'appliquent à des idéaux par opposition à des objets sensibles ; il est naturel d'aller plus loin, et de soutenir que la pensée est plus noble que les sens, et que les objets de la pensée sont plus vrais que ceux perçus par les sens.
Les doctrines mystiques sur la relation entre temps et éternité sont aussi renforcées par les mathématiques pures, car les objets mathématiques, comme les nombres, s'ils ont une quelconque réalité, sont éternels, et non des choses sur lesquelles le temps a prise. De tels objets éternels sont conçus comme des pensées de Dieu. D'où la doctrine de Platon selon laquelle Dieu est un géomètre, et la conviction de Sir James Jean qu'Il a une addiction à l'arithmétique. La religion rationnelle, par opposition à apocalyptique, a été depuis Pythagore, et surtout depuis Platon complètement dominée par les mathématiques et la méthode mathématique.
Mélange entre science et mysticisme
La combinaison des mathématiques et de la théologie, qui commença avec Pythagore, caractérisera la philosophie religieuse dans l'Antiquité grecque, au Moyen Âge, et dans les temps modernes jusqu'à Kant. L'Orphisme avant Pythagore était analogue aux religions fondées sur un Mystère ["asiatiques" veut dire, je crois, persanes et des régions avant l'Hindou Kouch].
Mais dans Platon, Saint Augustin, Thomas d'Aquin, Descartes, Spinoza et Kant, il y a un mélange intime de religion et de raisonnement, d'aspirations morales et d'admiration logique pour ce qui est intemporel. Tout cela vient de Pythagore, et distingue la théologie intellectualisée européenne du mysticisme plus simple asiatique.
C'est seulement à une époque tout à fait récente [au début du XXe siècle, grâce à la nouvelle physique, qui a développé au-delà de l'imaginable "les deux petits nuages dans l'édifice complet et parfait de la Physique" dont parlait encore Lord Kelvin lors d'une célèbre conférence à Londres en 1900 -- on attend encore la grande conférence du début du XXIe siècle... Lire Edward Witten peut-être...] qu'il a été possible de dire clairement que Pythagore se trompait.
[Russell veut sans doute dire qu'en réalité il n'existe pas de monde "idéal" autre que ce que nous construisons dans notre esprit, et utilisons pour modéliser nos perceptions. R. contredit plutôt Platon que Pythagore, qui était trop mystique pour être clair, et de toute façon n'est connu qu'à travers les présentations de Platon et surtout Aristote. Nous en apprendrons plus sur l'approche par les grecs anciens de cette question. Nous verrons en particulier l'emploi abusif qu'ils faisaient du verbe "exister".]
Je ne connais aucun autre homme qui ait été aussi influent que lui dans la sphère intellectuelle. On peut dire cela car il est clair, quand on l'étudie bien (comme nous le ferons), que le Platonisme est dans son essence pythagoricien. Toute la conception du monde éternel, révélé non à nos sens mais à notre intelligence, vient de Pythagore. Sans lui, les chrétiens n'auraient pas pensé au Christ comme étant le monde ; sans lui, les théologiens n'auraient pas cherché des preuves de l'existence de Dieu.
Mais dans Pythagore tout cela est encore implicite. Comment c'est devenu explicite est ce qu'on va voir.