Elementary finance
Random experiment
Text
introduction
long term stability
example 1: a drawer of socks
reproduction of a series of experiments
example 2: a wheel of chance
numerical measures, and average
law of large numbers
terminology and notations
simplicity and complexity of probabilities
an example of paradox
We are all familiar with situations in life where we can note or measure some feature, and also:
- we can reproduce the situation
- the values noted or measured, from one reproduction of the situation to the next, may be different
If you feel uneasy talking about something "which changes all the time", notice that when we consider objects in a room, we are not disturbed by the fact that their actual location may change from time to time (when we move them from the table to the shelf of books for instance, or when we take them in our hands).
Yet some fascinating long term stability is observed: if we reproduce the situation many times, the actual values taken by the feature noted or measured will show stability, in the sense that we shall describe.
Example 1: Suppose we have a chest of drawers, with socks in the bottom drawer
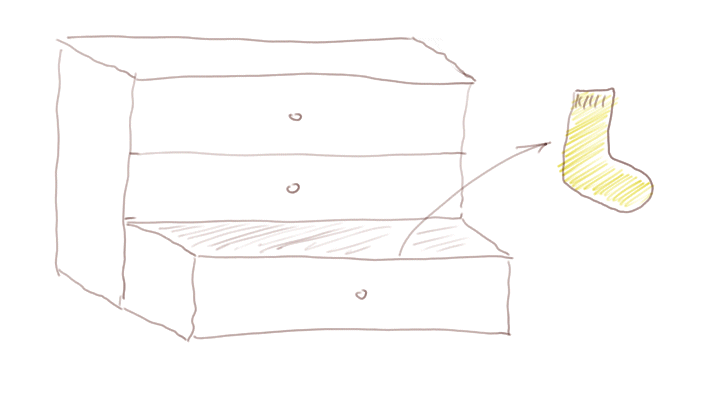
we pick a sock "at random" without looking into the drawer. Here we picked a yellow sock.
We put it back, and then pick again a sock at random.
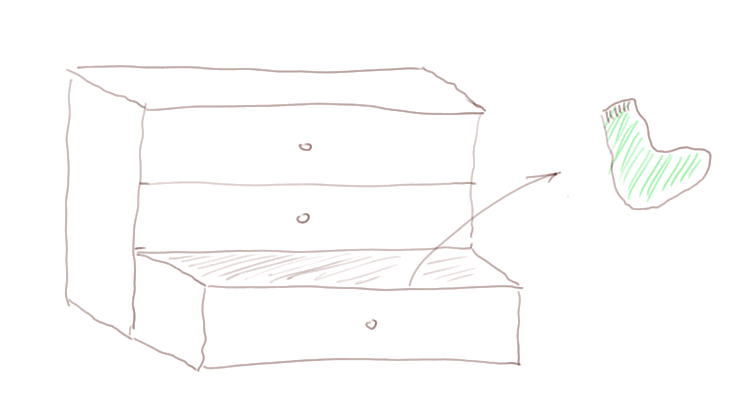
Now we picked a green sock. We put it back again.
If we reproduce the same experiment many times, we shall get a sequence (or series) of colours, with a certain proportion of yellow, a certain proportion of green, of black, of red perhaps (we assume that we don't know a priori what's in the drawer).
Next day, we ask a friend to perform the same series of experiments with the same chest of drawers. She will not get the same series of colours, but she will get roughly the same proportions.
That is the stability we were talking about.
Example 2:
We build a "wheel of chance". It is a disk which can turn around an axle fixed to a frame. On the frame, fixed too is an index.
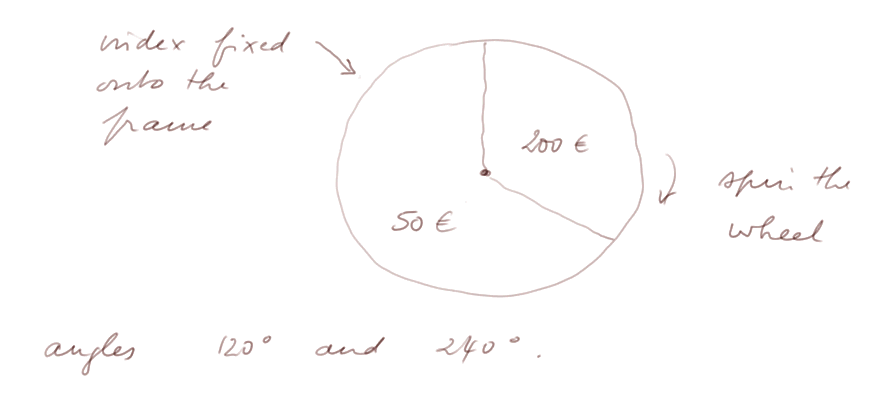
We mark two sectors, one with angle 1/3 of the disc, the other with angle 2/3. The first sector carries the value 200€, and the second 50€.
The random experiment is "spin the wheel", and the value we record at the end of a spin is the sum of money in the sector on which the index points.
If we spin the wheel many times, we shall get a sequence of outcomes. For instance:
200, 50, 50, 200, 50, 50, 50, 50...
The proportion of 50€'s and 200€'s will be "stable" in the sense that if we produce, the next day, a second long sequence of spins and measures, we shall get approximately the same proportions.
We can even telephone a friend, and ask him to build the same device, and perform a series of experiments. Again, he won't get the same series of results, but he will get approximately the same proportions as us.
In this second example, what we record is a number (the sum of money), so we can do calculations.
For instance we can compute the average result in a long sequence of spins. We shall always (we, as well as our friend) get roughly 100€.
The stability of the proportions, and of the average, are instances of what is called "the law of large numbers". We shall see in a later lesson that it has a simple and strong explanation, without any magic.
Terminology and notations:
- the production of the situation is called "the experiment". It is usually noted
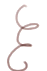 .
.
- the feature we note or measure (when it is numerical) is called a "random variable". It is usually noted X. When we measure several random variables at the end of one experiment, we note them X, Y, Z...
- the set of possible values of the random variable X, when it is discrete, will be denoted
A = { a1, a2, .... am }
- an instance of the RV (= random variable) X, that is an actual measure at the end of
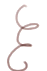 , will be denoted x. It is also called an "outcome" of X.
, will be denoted x. It is also called an "outcome" of X.
- if we reproduce
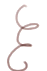 several times (say a large number N of times), the series of outcomes of X will be denoted
several times (say a large number N of times), the series of outcomes of X will be denoted
x1, x2, x3,... ... ... xN
each xi being a possible outcome, that is belonging to the set A.
We try to make probabilistic settings as simple as possible. But one must admit that it takes some time and thinking before we feel at ease with it.
There are plenty of apparent paradoxes. We finish this lesson with one of them.
Consider the following game: there are three doors, A, B and C.
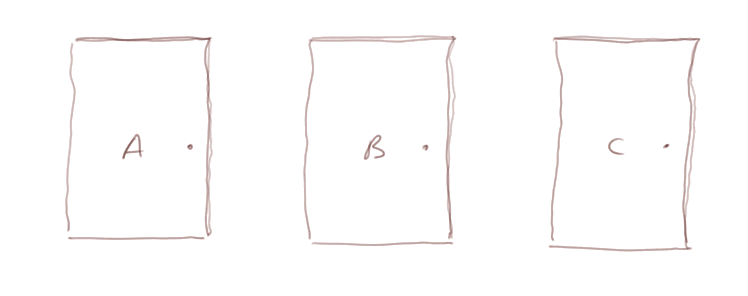
Behind one of them, there is a prize. You have to try and guess where, in order to win it.
Suppose you guess "door A".
Then before we check, the master of the game, who knows where the prize is, opens one of the 2 other doors where the prize is not. Say he opens B.

Now, to finish up the game, you are invited to guess again, if you want.
Question: should you change your guess (from A to C) or it doesn't matter?
Answer: you should change your guess and now guess C.
Screens of the video
|
|
|
screen number display zone |
Course table of contents
Contact