Cours de mathématiques de 6e27. Angles et triangles |
|
|
|
|
Video |
|
Texte
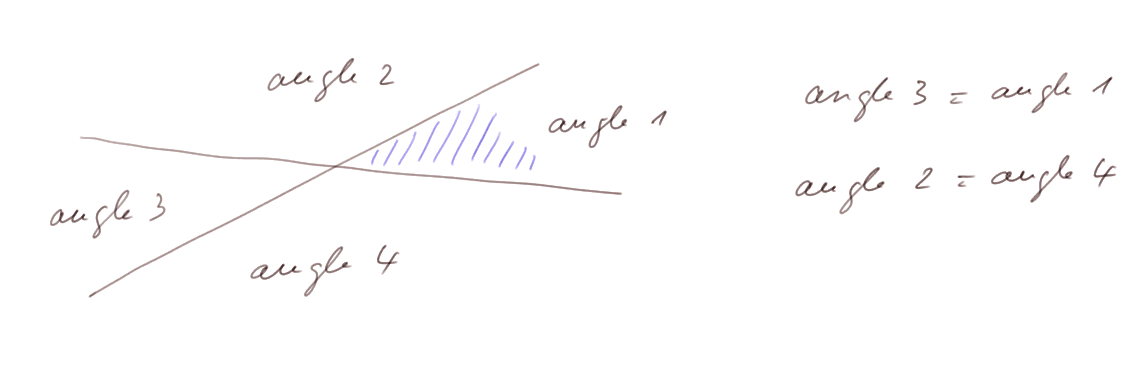
Un angle est une portion de plan délimitée par deux droites qui se coupent. A vrai dire ça fait 4 angles, donc il faut bien préciser duquel on parle.
Première propriété des angles délimités par deux droites : si les quatre angles s'appellent a1, a2, a3 et a4 comme sur la figure ci-dessous, alors on a a1= a3 et a2 = a4.
Quand on considère l'angle formé par deux droites, bien préciser duquel on parle.
On mesure les angles avec un rapporteur.
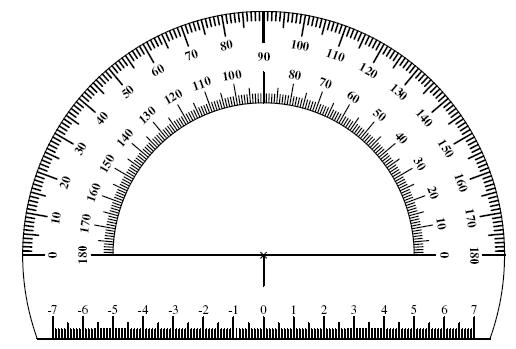
si on veut mesurer l'angle dans le sens contraire des aiguilles d'une montre, il faut utiliser les graduations internes
On place l'horizontale du rapporteur contre une des droites, avec le centre du rapporteur sur le point d'intersection. Ainsi on peut mesurer l'ouverture des deux droites, c'est-à-dire l'angle qu'elles forment.
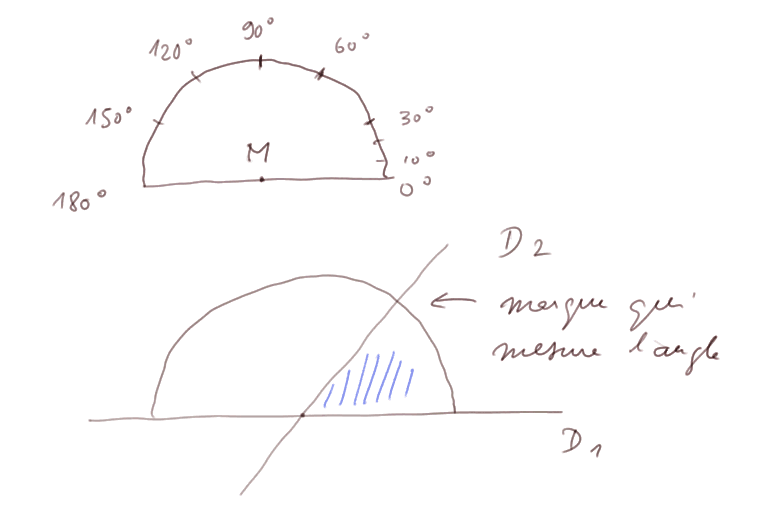
L'angle hachuré bleu fait environ 45°
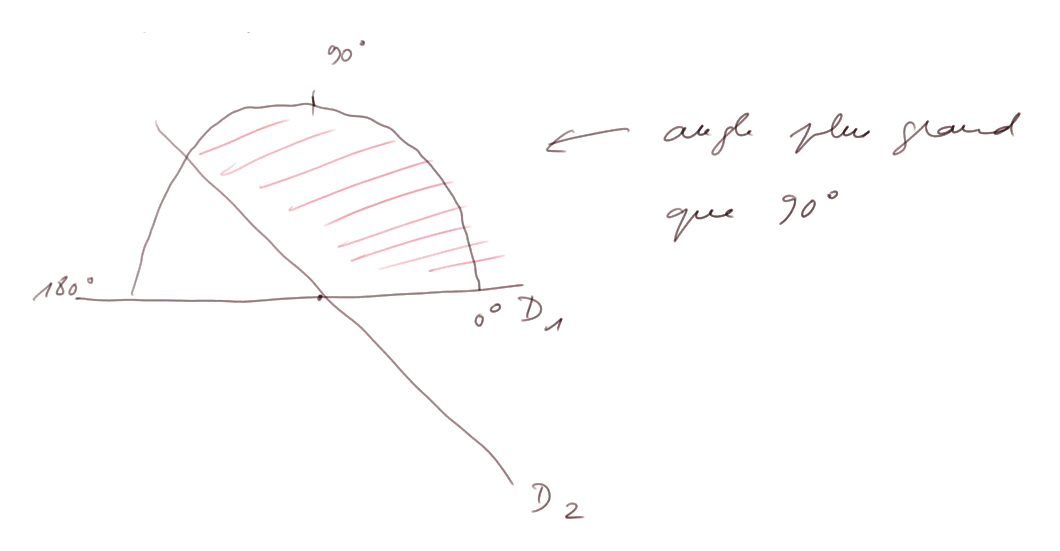
Les angles peuvent être plus grands que 90°, et même plus grands que 180°.
Quand deux droites se croisent, les angles adjacents font toujours 180°.
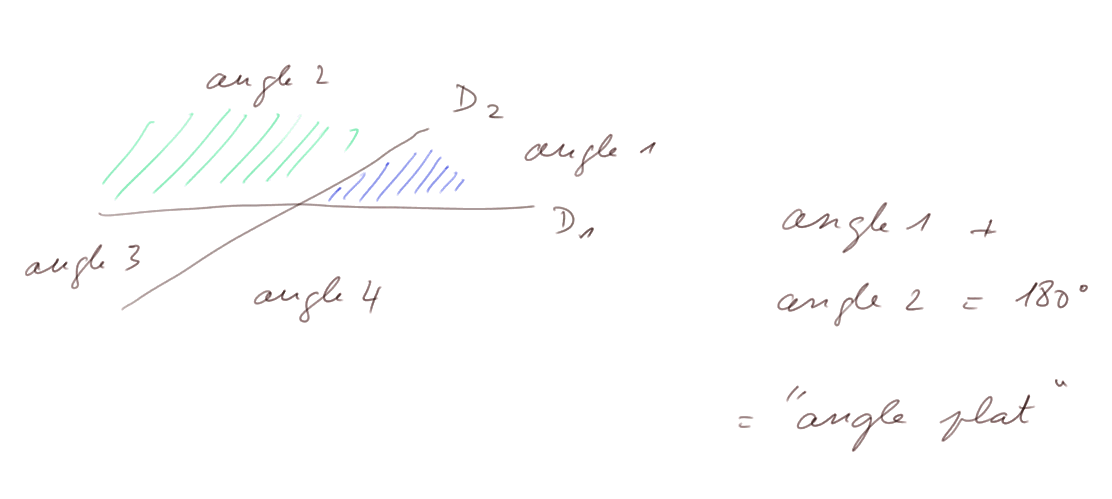
Droite qui coupent deux parallèles (on dit encore "droite sécante à deux parallèles") : une droite qui coupe deux parallèles crée 8 angles. Dans ces 8 angles, 4 ont la même mesure, et les 4 autres ont la mesure complémentaire pour faire 180°.
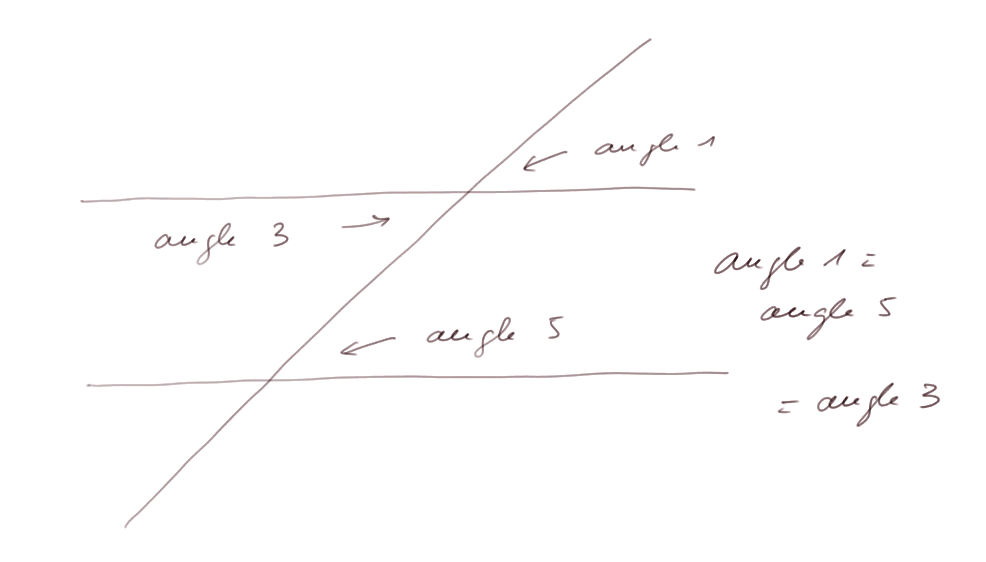
Droite sécante à deux parallèles : les angles 1, 3 et 5 sont égaux
On utilisera souvent cette propriété dans l'étude de différentes figures. Pour l'instant elle va nous servir à montrer le résultat important ci-dessous concernant les trois angles d'un triangle.
Un triangle est une figure du plan formée de trois points et les segments qui les joignent. Il y a trois angles, c'est pour cela qu'on appelle la figure un triangle. On aurait pu appeler les triangles "les tricôtés" (mais on aurait risqué de confondre avec les pullovers :-).
Dans un triangle quelconque, la somme des trois angles internes fait 180°. Pour montrer cela on trace passant par B une droite parallèle à AC, et en raisonnant sur les égalités entre angles, on voit immédiatement que les trois angles du triangle, sont égaux à trois angles autour de B dont la somme fait un angle de 180°, dit "angle plat".
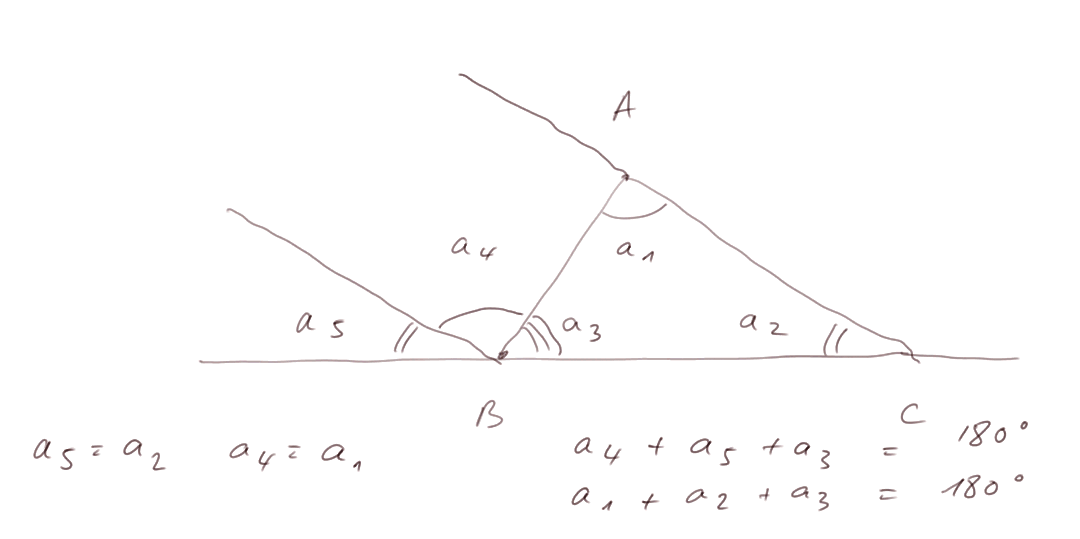
La somme des angles internes d'un triangle fait 180°
Attention : cette propriété est vraie sur un plan, mais pas toujours sur une surface bombée. Par exemple, elle n'est pas vraie sur la terre pour des triangles très grands. Elle n'est pas toujours vraie non plus sur un ballon de foot, ni à l'intérieur de l'écuelle concave dans laquelle mangent mes chats.
Les triangles ont des quantités de propriétes extraordinaires. Ils ont été abondamment étudiés par les Grecs. Voici une belle propriété due à Héron d'Alexandrie (c. 10 après JC, c. 70 après JC).
Appelons a, b et c les longueurs des trois côtés d'un triangle, et s son demi périmètre, c'est-à-dire s = (a + b + c) / 2. Et appelons A l'aire du triangle. On sait depuis l'école primaire qu'on peut la calculer comme la base multipliée par la hauteur divisée par 2.
Formule de Héron : ce mathématicien grec a montré que A x A = s x (s - a) x (s - b) x (s - c). Ce n'est pas une démonstration du niveau de sixième, mais cela ne nous empêche pas de connaître la formule et d'apprécier sa beauté. Pour un mathématicien, c'est une très belle formule, car elle calcule une aire sans passer par la multiplication d'une longueur par une autre longueur perpendiculaire.
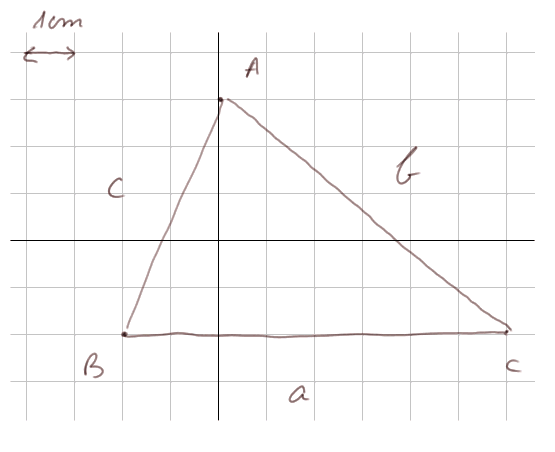
Vérifions-la sur un exemple :
|
Dans le triangle ci-dessus, a = 8 cm, et avec notre double-décimètre on peut mesurer b ≈ 7,81 cm, et c ≈ 5,39 cm. D'où s ≈ 10,6 cm.
D'après la formule de Héron, A x A ≈ 10,6 x 2,6 x 2,79 x 5,21 (la formule de Héron est exacte, mais comme mes mesures sont approximatives, je mets le signe ≈). Le calcul donne A x A ≈ 400,6.
Par ailleurs, en prenant pour base BC = 8 cm, et hauteur le segment partant de A et perpendiculaire à BC (hauteur = 5 cm), on calcule que A = (8 x 5) / 2 = 20.
Enfin 20 x 20 = 400. Donc on a vérifié approximativement (mais néanmoins de manière assez précise) la formule de Héron.
Exercices
- Quelle est la valeur de chaque angle d'un triangle équilatéral ?
- On a un triangle isocèle dont l'angle différent des deux autres est 40°. Quelle est la valeur des deux autres ?
- On a un triangle rectangle dont l'un des angles non rectangle (c'est-à-dire différent de 90°) vaut 40°. Quelle est la valeur de l'autre ?
- Tracer sur une feuille de papier quadrillé, le triangle formé des points A = (2 ; 1), B = (7 ; 2) et C = (3 : 5). Avec votre double-décimètre, mesurer précisément les longueurs de AB, AC et BC, ainsi qu'une hauteur. Calculer l'aire du triangle par la formule habituelle. Et calculer l'aire du triangle avec la formule de Héron.
Plan général du cours
Contacter le professeur
Réponses
- Quelle est la valeur de chaque angle d'un triangle équilatéral ? Rép : 60°.
- On a un triangle isocèle dont l'angle différent des deux autres est 40°. Quelle est la valeur des deux autres ? Rép : 70°.
- On a un triangle rectangle dont l'un des angles non rectangle (c'est-à-dire différent de 90°) vaut 40°. Quelle est la valeur de l'autre ? Rép : 50°.