Cours de mathématiques de 6e1. Principes guidant le cours |
|
Video |
Nous avons déjà appris à l'école primaire l'utilisation pratique de toutes les notions qui seront à nouveau abordées dans ce cours de 6e : nombres entiers, quatre opérations arithmétiques, fractions, figures élémentaires de la géométrie du plan, lignes droites, rectangles, triangles, etc. Ce cours est donc essentiellement une révision des concepts appris entre le CP et le CM2.
Mais pour nous ce sera davantage. Ce sera aussi l'occasion de reconsidérer avec plus de profondeur ce que nous avons appris, en commençant par les nombres.
Un thème central de ce cours de mathématiques d'entrée au collège est de ne pas confondre les notions mathématiques avec leurs notations. Douze peut se noter XII, 12, 1100 ou avec douze petits cailloux, on parle toujours de la même chose.
Nous introduisons aussi les représentations (ou utilisations, ou modèles) des notions mathématiques. C'est même comme cela qu'on commence par les expliquer. Une représentation naturelle des nombres est une demi-droite avec des marques tous les centimètres correspondant aux nombres (*).
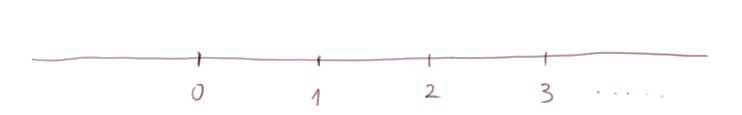
Nous verrons qu'une même notion peut avoir plusieurs représentations, et donc être utile dans des situations différentes. C'est toute l'essence des mathématiques. La division par exemple peut correspondre à un partage de quelque chose en plusieurs parties égales selon une certaine mesure ; ça peut aussi correspondre à une pente (une hauteur dont on s'élève en marchant le long d'un chemin, divisée par la distance horizontale parcourue) ; d'une manière plus générale ça peut correspondre à une densité (masse volumique, salaire horaire, pression, etc.) ; et encore à beaucoup d'autres choses.
Dans les sections sur les nombres, nous utilisons un peu les chiffres romains. Ils montrent ce qu'est un mauvais système de notation des nombres, et ils permettent de bien comprendre la différence entre les nombres et leurs notations. Nous posons la multiplication LVII x XIII dont le résultat est DCCXLI pour illustrer le manque de commodité de la notation en chiffres romains. Ceci nous amène naturellement au système des chiffres arabes.
En ce qui concerne les notations algébriques et les priorités, nous pensons qu'un enfant de 11 ans accepte sans se poser trop de questions que dans une formule comme 2 x 3 + 4 la convention la plus répandue est d'effectuer la multiplication avant l'addition. Et donc 2 x 3 + 4 = 10 et non 14. Les règles formelles sont introduites seulement en cinquième. Dans ce cours de sixième nous utilisons librement de temps à autre des parenthèses sans en faire un sujet important.
La notion de preuve en géométrie élémentaire n'a rien d'élémentaire. Elle a beaucoup occupé les plus grands mathématiciens il y a environ un siècle. Il faut éviter, dans les explications aux enfants, les raisonnements circulaires du genre : la proposition A est vraie car elle découle de B. B est vraie car elle découle de C. Et C est évidemment vraie car... elle découle de A.
Nous préférons utiliser quelques "vérités géométriques".
- Deux droites parallèles coupées par une troisième forment deux collections de 4 angles égaux. On le justifie en faisant glisser une équerre le long de la droite sécante.
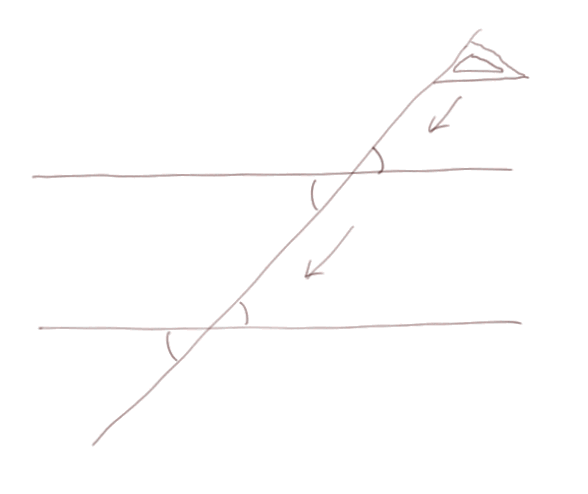
Qu'il y ait cachés sous cette "vérité géométrique" les axiomes du plan (car cette vérité géométrique n'est pas vraie sur une sphère) ne nous concernera pas dans ce cours.
-
Si on a deux segments AB et DE de longueur égale, et qu'on construit deux triangles en prenant respectivement les mêmes angles, alors les triangles ABC et DEF sont "égaux" au sens de superposables. Et en particulier on a AC = DF et BC = EF.
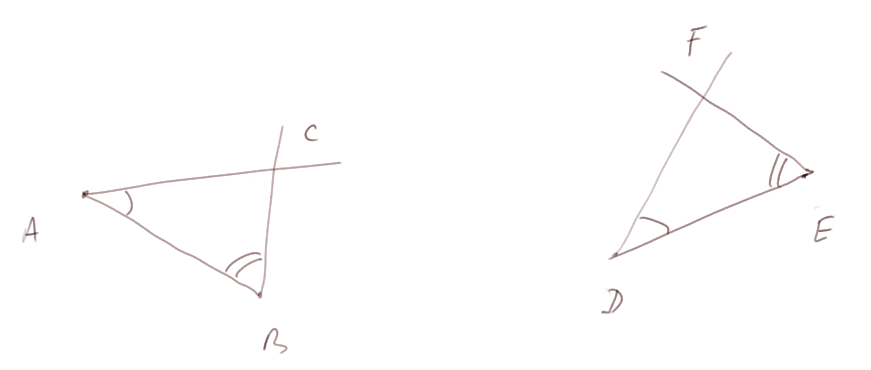
- Troisième vérité géométrique, dans un parallélogramme (défini comme une figure à quatre sommets dont les côtés opposés sont parallèles), les côtés opposés sont égaux, et les diagonales se coupent en leur milieu. (On pourrait d'ailleurs déduire cette troisième vérité géométrique des deux précédentes.)
Nous n'hésitons pas de temps en temps à montrer de belles choses d'un programme plus avancé, mais dont la beauté est compréhensible : par exemple, le dessin du théorème de Pascal sur les cercles.
Nous introduisons quelques points d'histoire, mentionnons Al Khawarizmi, Fibonacci, etc.
Le langage utilisé est aussi simple que possible. Mais nous cherchons à ne pas bêtifier non plus. Les exemples sont issus de la vie courante : un carreleur (pour des calculs avec la multiplication), une boîte de lait (pour illustrer les parallélépipèdes rectangles), etc.
De même que le Cours préparatoire pose les bases pour des années d'apprentissage de la lecture, de l'écriture et du calcul, nous posons les bases pour des années de cours de maths utiles et intéressants.
Apprendre en jouant
Dans l'enseignement français à l'école maternelle on apprend en jouant. La maîtresse donne des cubes, des bûchettes et d'autres objets et invite les petits écoliers à faire joujou avec, sans les guider spécialement.
Mais ensuite dès le CP les écoliers sont pris en main et l'enseignement consiste alors pour les douze années suivantes à ingurgiter des savoirs et des règles. Les écoliers ne jouent plus. Ils apprennent que a² - b² = (a+b)(a-b), et d'autres choses comme ça, mais sont stupéfaits vingt ans après la fin de leurs études d'observer que 9 x 7 = 63 est lié au fait que 8 x 8 = 64 (si on a fait joujou avec la formule ci-dessus et observé par exemple que 9 = 8 + 1 et 7 = 8 - 1). On ne les a plus encouragés à jouer par eux-mêmes avec les formules qu'ils ont ingurgitées.
Nos cours encouragent vivement les élèves à jouer eux-mêmes avec les notions présentées. C'est la seule façon de commencer à vraiment comprendre et apprécier les mathématiques tant pour leur beauté que pour leur utilité.
Les maths devraient être enseignées par ceux qui les utilisent
Idéalement les maths ne devraient pas être enseignées par des profs de maths mais par des profs ou des gens qui s'en servent : profs de physique, d'informatique ou de technologie, ingénieurs qui viendraient donner un cours.
Imaginerait-on un cours d'ébénisterie enseigné par quelqu'un qui n'aurait jamais construit de meuble, ou un cours de conduite par quelqu'un qui n'aurait pas de voiture ? C'est pourtant la situation de la plupart des disciplines dans l'enseignement secondaire en France. Cela ne veut pas dire qu'il ne faut pas de profs de maths, mais qu'ils devraient d'abord être des profs de disciplines dans lesquelles les maths sont utilisées, ou qu'ils aient une activité en ingéniérie à côté de leur enseignement.
L'un des drames de l'enseignement des mathématiques en France est que les élèves ne voient pas à quoi ça sert. Les enseignants qui ne connaissent que les maths ne sont pas les mieux placés pour montrer aux élèves qu'elles sont utiles. Un jour je demandais à un prof de maths à quoi servait d'apprendre l'intégrale de Lebesgue (**) ; il me répondit après un long moment de réflexion : "Eh bien, si vous devez l'enseigner."
Notre approche est différente : nous cherchons à montrer que les mathématiques servent dans la vie courante.
Une dernière note sur l'enseignement public en France.
Plan général du cours
Contacter le professeur
Notes de bas de page
* Comme dans ce modèle on fait correspondre les nombres aux marques à la fin de chaque centimètre, mais on peut aussi "compter" les centimètres eux-mêmes, certaines personnes, même adultes, sont troublées par le fait que le premier centimètre est situé avant la marque 1. De même les années du XXe siècle commencent toutes sauf une par 19... - sauf une, car l'année 2000 est aussi une année du XXe siècle.
** Evidemment, l'intégrale de Lebesgue sert si on veut devenir mathématicien, car elle est issue de la théorie de la mesure qui clarifie profondément la notion d'espace, et permet d'aborder des structures de plus en plus abstraites. Mais elle ne sert même pas pour devenir ingénieur mathématicien de haut niveau en hydrodynamique, ou pour devenir physicien classique ou quantique.