Cours de mathématiques de 1ère SProduit scalaire de deux vecteurs |
|
|
|
|
Video |
|
Texte
Soit deux vecteurs V = (a, b) et W = (c, d) dans le plan. On définit le produit scalaire de V et W comme le nombre ac + bd. Nous allons montrer que derrière cette jolie formule se cachent des choses extrêmement simples. On va en particulier établir que V et W sont perpendiculaires si et seulement si leur produit scalaire est égal à zéro.
D'une manière générale, on peut dire que 80% des maths du collège et du lycée sont "les maths de la feuille quadrillée". Le produit scalaire va nous permettre de l'illustrer.

la feuille quadrillée, base de 80% des maths du collège et du lycée
Qu'est-ce qu'un vecteur ? Réponse : c'est un déplacement d'une certaine longueur dans une certaine direction.
C'est donc une fonction dans le plan qui a tout point P du plan associe un point Q, "transformé de P", par un déplacement. Travaillons par exemple avec le vecteur V = déplacement de 3 unités vers la droite et de 5 unités vers le haut.
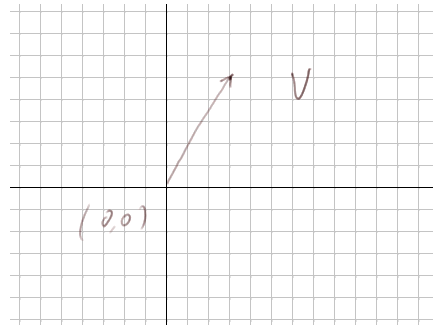
Voici le vecteur appliqué au point (0, 0), il l'emmène vers le point (3, 5), et il est de coutume de représenter le vecteur par une flèche comme sur le dessin ci-dessus. Mais le vecteur n'est pas cette flèche. Celle-ci en est juste une représentation commode : (0, 0) et son transformé (3, 5).
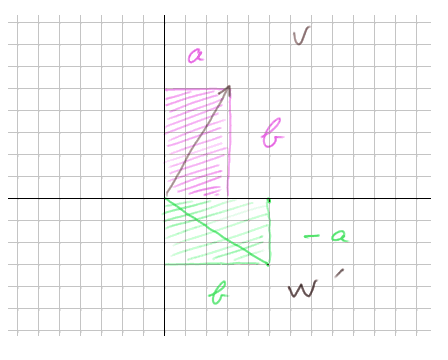
Identifions momentanément le vecteur V à la diagonale du rectangle rose :
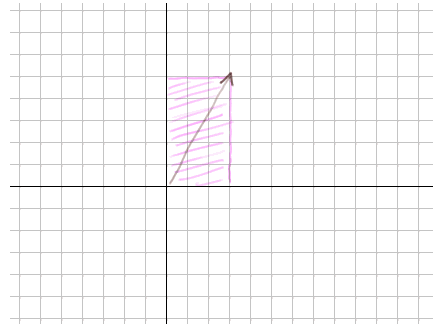
Pensez à ce rectangle comme à un petit morceau de bois libre qu'on a calé contre les axes.
Si on fait pivoter le rectangle de 90° dans le sens positif (et on pourrait aussi le faire dans le sens négatif), on peut encore le caler contre les axes, avec le point (0, 0) qui n'a pas bougé.
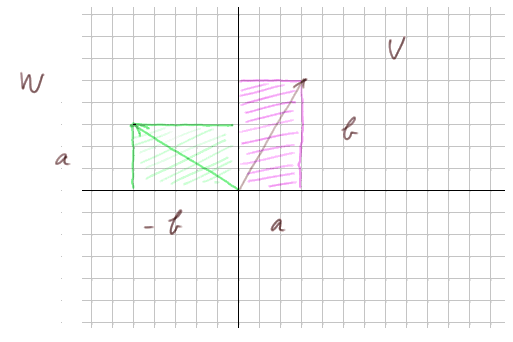
Le vecteur W obtenu est perpendiculaire à V et a pour coordonnées (-b, a).
On observe que le produit des abscisses + le produit des ordonnées de V et W fait 0 :
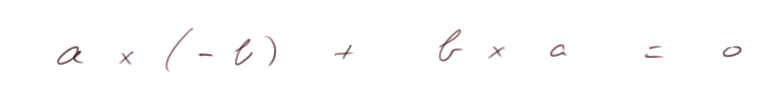
D'une manière générale, si un vecteur W est perpendiculaire à V, il transforme le point (0, 0) en un point sur la droite verte ci-dessous :
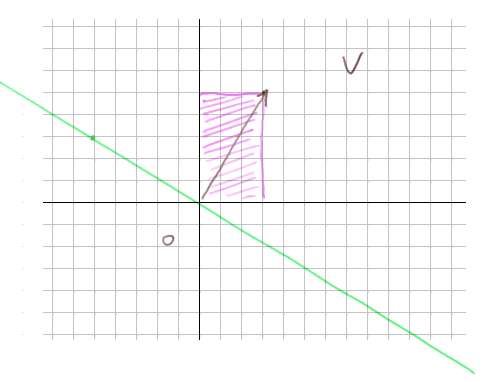
W est donc un multiple de (-b, a), c'est-à-dire que W a pour coordonnées (-λb, λa) où λ est un coefficient quelconque.
Donc pour tout vecteur W = (c, d) perpendiculaire à V = (a, b), on a (c, d) = (-λb, λa), et donc
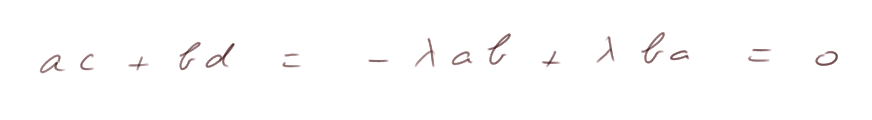
Réciproquement, prenons deux vecteurs V = (a, b) et W = (c, d) quelconques (de longueur non nulle). Montrons que
si ac + bd = 0 alors V et W sont perpendiculaires
Considérons a priori les deux vecteurs V et W comme ci-dessous :
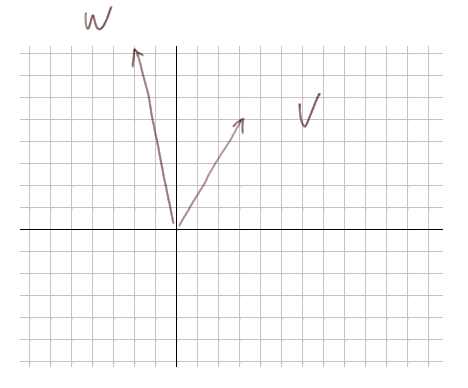
On va allonger ou raccourcir W afin d'obtenir un vecteur W' dont l'abscisse est égal à b.
(C'est toujours possible si W n'est pas vertical. Quant au cas où W est vertical, ac + bd = 0 implique alors que b doit être égal à zéro, donc V est horizontal et perpendiculaire à W.)
Le coefficient d'allongement ou de raccourcissement de W pour obtenir W' est λ = b/c.
W' = (c', d') = (b, d'). Comme on avait ac + bd = 0, en multipliant par λ, on a aussi ac' + bd' = 0, c'est-à-dire
ab + bd' = 0, donc forcément d' = -a.
Donc W' est bien perpendiculaire à V, et donc W aussi (car c'est juste un allongé ou un raccourci de W').
On a donc établi le résultat fondamental suivant: deux vecteurs V = (a, b) et W = (c, d) sont perpendiculaires si et seulement si leur produit scalaire est égal à zéro.
Ce résultat simple est la conséquence de propriétés élémentaires d'un quadrillage ou d'un carrelage.
Il se trouve qu'il est aussi très puissant. On sera amené à l'utiliser dans de nombreuses circonstances.
Plus tard on considérera même des espaces plus abstraits que notre feuille quadrillée. Ce seront des "espaces de vecteurs", "munis d'un produit scalaire", permettant de définir des notions de distance et d'orthogonalité. Ce sera le cas par exemple des variables aléatoires dans une expérience. Mais en première S introduire le produit scalaire comme une opération particulière au sein d'un espace vectoriel quelconque ne peut que créer de la confusion. Il faut d'abord bien comprendre que c'est une notion simple issue des marelles et jeux de cube de notre enfance.
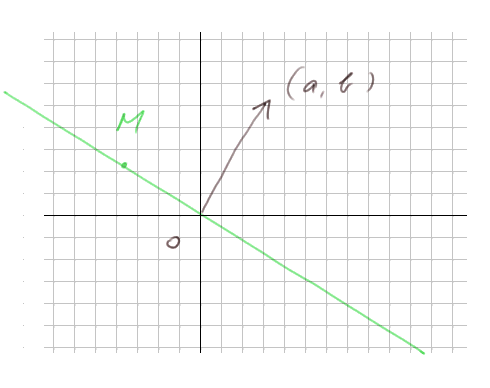
Pour finir, regardons l'équation d'une droite passant par l'origine. D égale tous les points (x, y) tels que ax + by = 0.
C'est une contrainte sur un produit scalaire : ça impose produit scalaire de (x, y) et (a, b) = 0 ; c'est-à-dire les vecteurs OM = (x, y) et V = (a, b) doivent être perpendiculaires.
Voici le dessin de la droite :
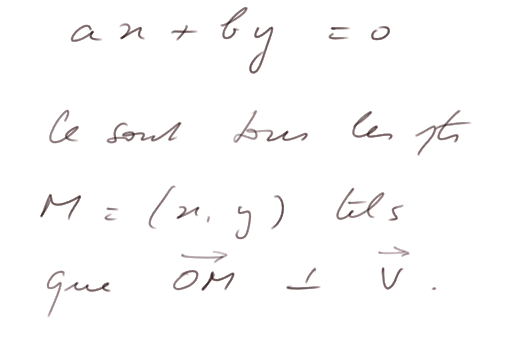
Regardons même une droite générale d'équation ax + by + c = 0.
Soit un point M0 = (x0, y0) sur cette droite. Alors ax0 + by0 + c = 0.
Retranchons cette égalité de l'équation de la droite, on obtient la nouvelle équation
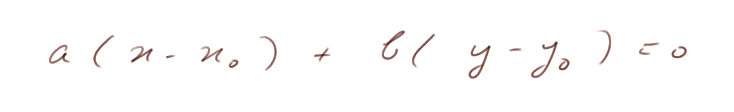
C'est à nouveau une contrainte sur un produit scalaire : le produit scalaire de V = (a, b) avec le vecteur ![]() doit être égal à zéro.
doit être égal à zéro.
Donc la droite d'équation ax + by + c = 0 est l'ensemble des points M tels que ![]() est perpendiculaire à (a, b).
est perpendiculaire à (a, b).
Conclusion : le produit scalaire est simple et utile. Nous verrons encore beaucoup d'autres propriétés (dont "la formule avec un cosinus"). Mais rappelons-nous surtout que ce qu'on vient de faire est des raisonnements élémentaires sur la feuille quadrillée.
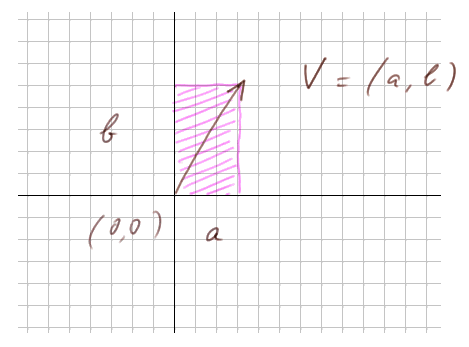
Une applet java pour illustrer le produit scalaire.
Les écrans de la vidéo
|
|
|
screen number display zone |