Cours de mathématiques de 3e

Principe de Cavalieri : application au calcul du volume de la sphère, puis calcul de sa surface

Texte

Principe de Cavalieri en 2 dimensions : Considérons 2 surfaces dans le plan, contenues entre 2 lignes droites parallèles D₁ et D₂.

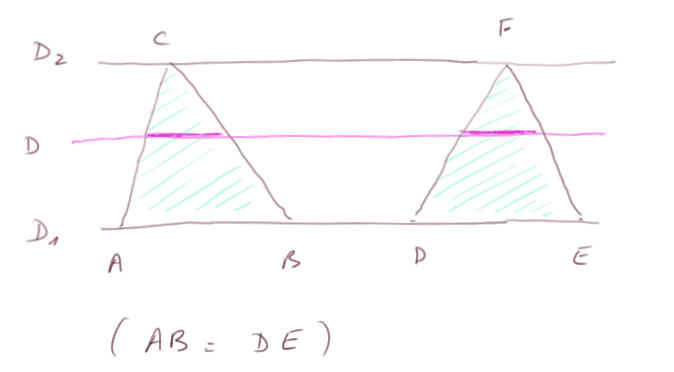
Si toute ligne droite D, parallèle à D₁ et D₂, coupe les 2 surfaces en segments de même longueur, alors les 2 surfaces ont la même aire.

Dans la figure d'illustration, nous avons représenté deux triangles, mais le principe est beaucoup plus général. Les surfaces peuvent avoir des formes quelconques, si elles restent raisonnables, et n'ont même pas besoin d'être d'un seul tenant.

Principe de Cavalieri en 3 dimensions : Considérons 2 volumes dans l'espace, contenus entre 2 plans parallèles P₁ et P₂.

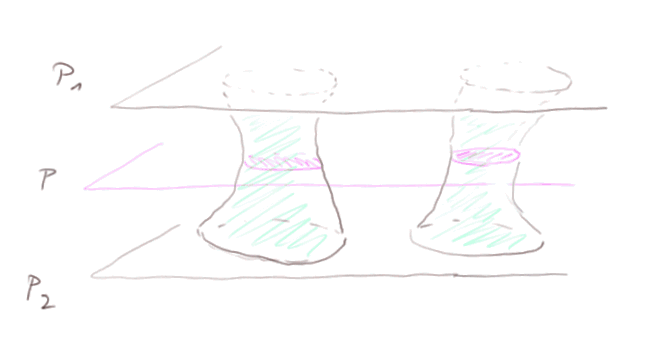
Si tout plan P, parallèle à P₁ et P₂, coupe les 2 volumes en surfaces de même aire, alors les 2 volumes sont de mesure égale.

Dans la figure ci-dessus, les surfaces ont gardé leur forme, mais là encore ce n'est pas nécessaire : les volumes peuvent prendre des formes quelconques.

On a appliqué ce principe pour calculer le volume d'une pyramide quelconque (voir leçon sur les pyramides), à partir de celle qui découpait un cube en 3 parties identiques.

Application au calcul du volume de la sphère : Le principe de Cavalieri (mathématicien italien, 1598 - 1647) permet de calculer de manière élémentaire le volume de la sphère !

Considérons une sphère de rayon "r" (à droite), et un cylindre de hauteur "r" et de base circulaire de rayon "r", et le cône renversé inscrit dans le cylindre comme sur la figure ci-dessous :

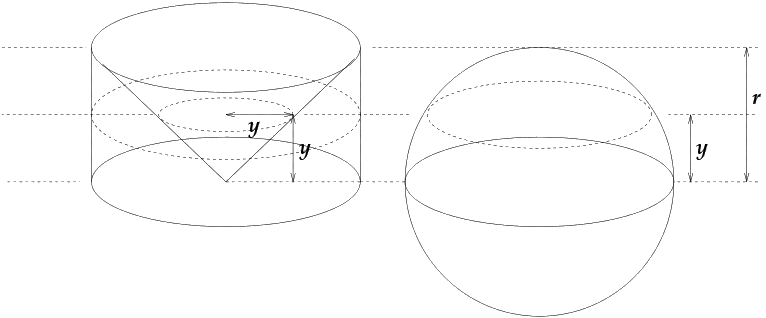
source : Wikipedia en anglais, article sur le principe de Cavalieri

Les deux surfaces roses, ci-dessous, ont la même aire :

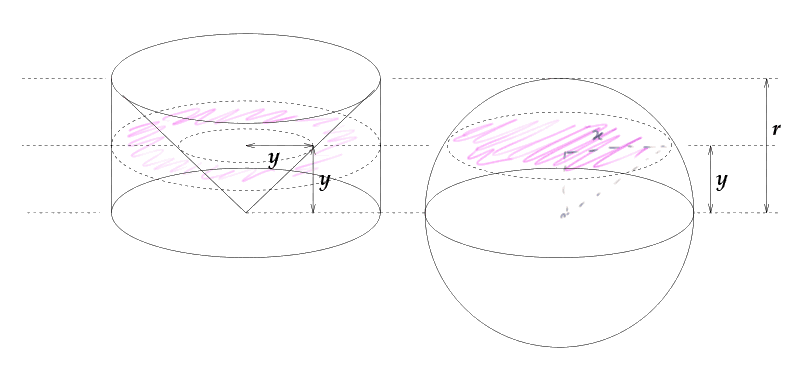
En effet l'anneau rose de gauche a pour aire Πr² - Πy², et le disque rose de droite a pour rayon "x" tel que x² + y² = r², donc son aire est Πx² = Πr² - Πy².

En vertu du principe de Cavalieri, le volume balayé par l'anneau rose, quand "y" passe de 0 à r, est le même que le volume balayé par le disque rose, quand "y" passe de 0 à r (c'est-à-dire l'hémisphère).

Le volume balayé par l'anneau rose est [ le volume du cylindre - le volume du cône ]. Ce dernier est 1/3 du volume du cylindre. Et le cylindre a pour volume r fois Πr².

Donc l'hémisphère a pour volume 2/3 de Πr³.

Pour conclure, le volume de la sphère de rayon r est

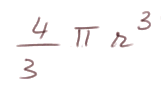
C'est une de ces formules importantes à connaître en mathématiques, comme la circonférence ou la surface du cercle.

Surface de la sphère : Du volume de la sphère, on déduit aisément sa surface. Découpons la surface de la sphère en une multitude de petites surfaces comme ci-dessous

Chaque petit élément "s" de surface, sur la surface de la sphère, détermine une petite pyramide de volume "v" = "s" x r x 1/3.

En additionnant toutes ces petites pyramides, on trouve que le volume de la sphère est égal à (r/3) fois sa surface.

D'où l'on déduit que la surface de la sphère est égal à son volume fois 3/r.

C'est-à-dire, la surface de la sphère est

C'est aussi une formule importante à retenir.

Exercices :

1. Montrer que le volume de la sphère est égal aux 2/3 du volume du cylindre circonscrit. (Ce résultat, dû à Archimède, était celui dont il était le plus fier.)
   
   

Les écrans de la vidéo

écran 1
écran 2
écran 3
écran 4
écran 5
écran 6
écran 7
écran 8

Plan général du cours

Contacter le professeur