Cours de mathématiques de 3eArithmétique : le théorème de Bezout |
|
|
|
|
Video |
|
Texte
Le théorème de Bezout est un résultat important d'arithmétique élémentaire dans la continuation de l'algorithme d'Euclide (qui sert à trouver le pgcd de deux nombres). Le théorème de Bezout est simple et très puissant. Son énoncé dit que si a et b sont deux nombres entiers positifs alors
- il existe deux entiers relatifs u et v tels que au + bv = pgcd(a, b)
- le pgcd de a et b est égal à 1 si et seulement si il existe deux entiers relatifs u et v tels que au + bv = 1
Voici deux exemples :
- soit a = 24 et b = 58, alors leur pgcd est 2, et on a 2 = 5 x 58 - 12 x 24.
- soit a = 8 et b = 875, alors leur pgcd est 1, et on a 1 = 3 x 875 - 328 x 8.
L'idée de la démonstration est d'utiliser l'algorithme d'Euclide "à l'envers".
Nous donnons ci-dessous la démonstration pour mémoire, mais il n'est pas important de la maîtriser. (Elle ne fait usage d'aucune technique avancée, mais elle peut néanmoins paraître difficile.) En revanche il est important de connaître ce que dit le théorème de Bezout. Nous serons amenés à l'utiliser à plusieurs reprises.
On prouve donc la première partie du théorème en utilisant l'algorithme d'Euclide. Soit a et b deux entiers positifs (avec mettons b > a), l'algorithme d'Euclide est simplement une série de divisions euclidiennes (qu'on va voir ci-dessous) jusqu'à ce qu'on obtienne un reste nul. Le dernier reste non nul est le pgcd de a et b :
On commence par la division de b par a : (1) b = p x a + c
Si "c" = 0, l'algorithme s'arrête, "a" est lui-même le pgcd. Si "c" est un reste non nul, alors on fait maintenant la division euclidienne de "a" par "c" : (2 ) a = q x c + d
De nouveau, si "d" est nul, "c" est le pgcd de a et c, et aussi de a et b, et l'algorithme s'arrête. Sinon, on fait la division euclidienne de "c" par "d" : (3) c = r x d + e
Et ainsi de suite.
Le dernier reste non nul est le pgcd de a et b.
Supposons ici qu'on a seulement dû faire trois divisions euclidiennes. (Le raisonnement est le même si on a dû en faire plus.) Alors e est le pgcd de a et b.
On va tout simplement partir de la dernière division euclidienne et "remonter" vers la seconde puis la première :
On réécrit la dernière division euclidienne comme ceci : e = c - rd
Et on y remplace d par sa formule donnée par la seconde : d = a - qc
Donc e = c - rd devient e = c - r(a - qc) = c(1 + rq) - ra.
Puis on remplace "c" par sa valeur en fonction de a et b donnée par la première division euclidienne.
On obtient e = (b - ap)(1 + rq) - ra.
Finalement nous avons "e" exprimé seulement à l'aide de a et b avec des coefficients devant. On réorganise un peu, et on obtient
e = b(1 + rq) - a(p + r + rpq)
C'est la forme finale promise par Bezout (ici dans le cas de trois divisions euclidiennes jusqu'au pgcd) : u = -(p + r + rqp) et v = (1 + rq).
Exemple 1 : calculons le pgcd de 58 et 24 (calculs en bleu), puis trouvons les coefficients u et v (calculs en rouge)
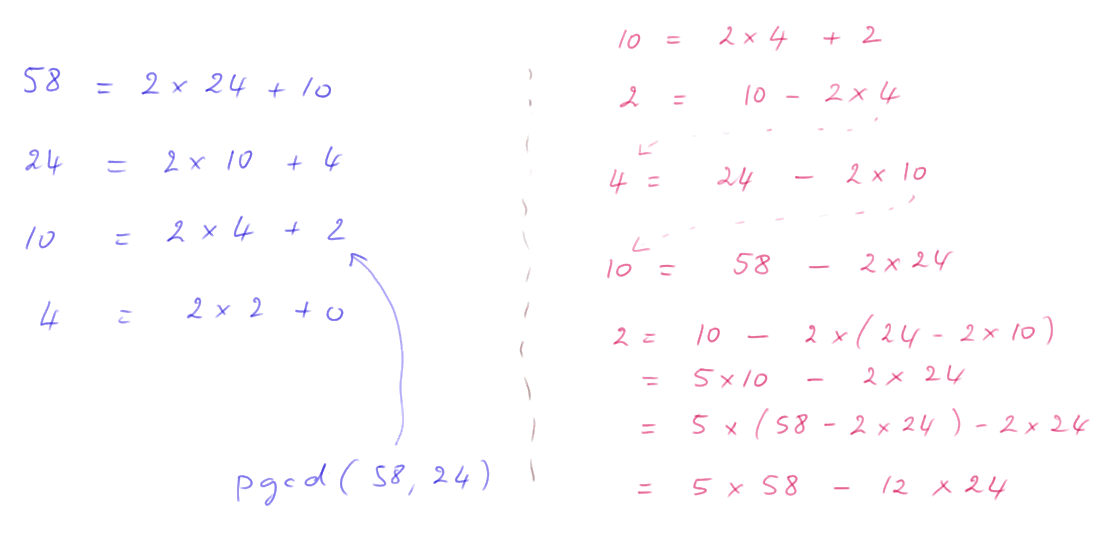
On peut vérifier que 5 x 58 = 290 et 12 x 24 = 288. Leur différence est donc bien le pgcd de 58 et 24.
Passons maintenant à la deuxième partie de l'énoncé du théorème de Bezout, qui parle du cas de figure où a et b sont premiers entre eux, c'est-à-dire, par définition, que leur pgcd est 1.
D'après ce qu'on vient déjà de démontrer, on sait qu'il existe u et v tels que au + bv = 1.
Réciproque : si au + bv = 1 pour une certaine paire (u, v), alors a et b ne peuvent pas avoir d'autre diviseur commun que 1, car un diviseur commun de a et b doit aussi diviser 1.
Exemple 2 : prenons a = 12 et b = 385.
L'algorithme d'Euclide démarre par 385 = 32 x 12 + 1. C'est donc déjà fini. Le pgcd est 1. Et l'identité de Bezout est immédiate, c'est la première division euclidienne réécrite : 1 = 385 - 32 x 12.
Exemple 3 : prenons a = 8 et b = 875.
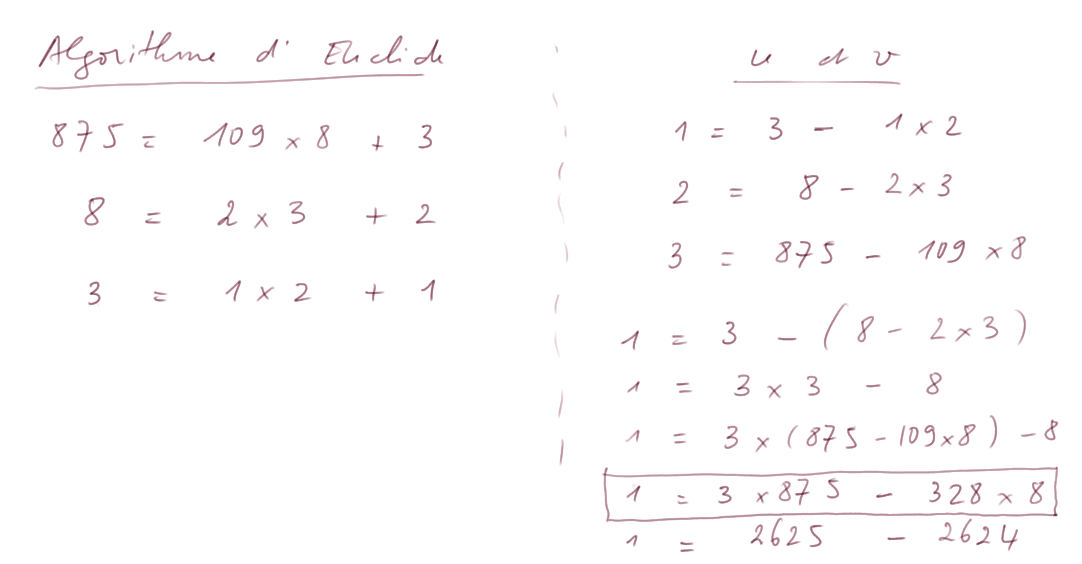
Exercice : Faire des calculs du même genre avec d'autres exemples de nombres a et b.