Cours de mathématiques de 6e

20. La règle de trois

Video

Texte

La règle de trois est une technique de calcul élémentaire permettant de résoudre des problèmes de proportions.

Pour comprendre de quoi il s'agit, illustrons-la par quelques exemples.

Premier exemple. Marion et Jules sont frère et soeur :

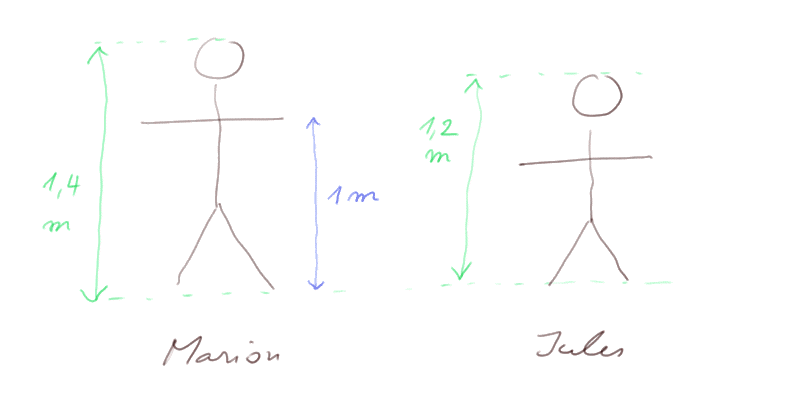
Supposons qu'ils aient exactement les mêmes proportions.

Qu'est-ce que cela veut dire pour deux figures d'avoir "les mêmes proportions" ? Dans le langage courant cela veut dire que l'une est "comme l'autre, en plus grand ou en plus petit". De manière plus mathématique, cela veut dire par définition que le rapport de n'importe quelle paire de distances prises dans l'une des figures est égal au rapport de la paire des distances correspondantes dans l'autre. Par exemple, la longueur d'un bras divisée par la hauteur de la tête donne le même résultat chez Marion et chez Jules.

Revenons à notre problème :

Les données du problème nous indiquent que Marion mesure 1 mètre 40 et Jules 1 mètre 20.

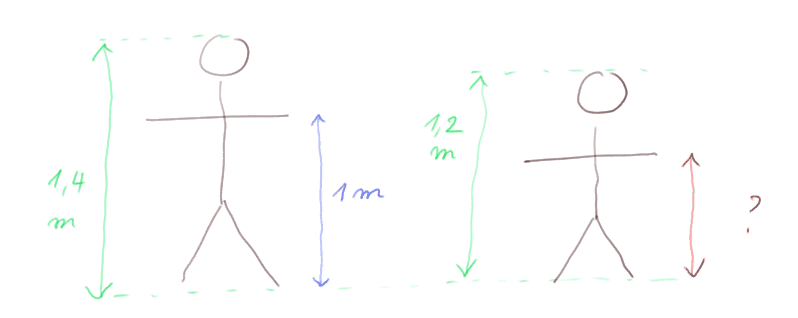
Et on sait aussi que quand Marion tient ses bras à l'horizontal, ses mains sont à 1 mètre du sol.

Question : à quelle hauteur sont les mains de Jules quand il tient ses bras à l'horizontal ?

Solution : Appelons "x" la hauteur où se trouve la main de Jules.

Alors la proportionnalité nous dit en particulier que "x est à 1,2 ce que 1 est à 1,4".

C'est-à-dire :

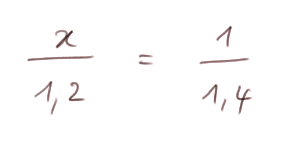
On fait un peu de calcul et on trouve :

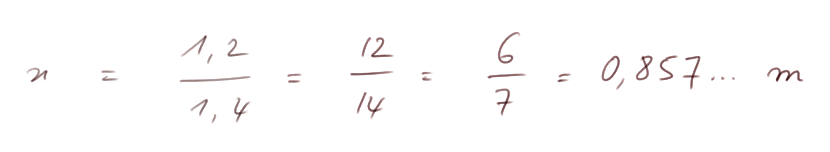
Donc la main de Jules est à 85,7 centimètres du sol.

Deuxième exemple. Il s'agit d'un problème posé au ministre de l'Education nationale, Xavier Darcos, au Grand Journal de Canal+, et qu'il n'a pas su résoudre.

Si 4 stylos coûtent 2€42, alors combien coûtent 14 stylos ?

Solution : Le coût d'un paquet de stylos est proportionnel au nombre de stylos qu'il y a dans le paquet.

Appelons "x" le coût de 14 stylos. Alors "x est à 14 ce que 2,42 est à 4".

C'est-à-dire que les deux rapports ci-dessous sont égaux :

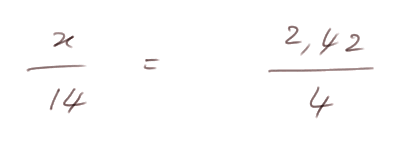
D'où l'on tire :

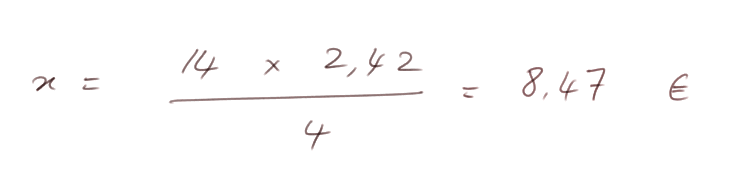
Notons que dans ce problème, on pourrait passer par le calcul du coût d'un stylo. On tomberait sur 0,605€, ce qui est un prix faisant intervenir des demi centimes. Donc les stylos de notre exemple sont vendus au moins par deux.

Divertissement : Le ministre aurait pu utiliser les additions et les soustractions seulement (à l'aide des logarithmes).

Tout nombre positif a un logarithme. Par exemple log 4 ≈ 0,60206.

Et deux nombres différents ont des logarithmes différents. On dit que la relation entre les nombres et leurs logarithmes est "biunivoque".

Ainsi si on connaît le logarithme d'un nombre, on peut retrouver le nombre lui-même (par exemple avec la calculette scientifique ci-dessus, ou avec des tables de logarithmes).

Les logarithmes ont une propriété merveilleuse : ils transforment les multiplications en additions, et les divisions en soustractions.

Si "c" est le produit de "a" par "b", alors (log c) = (log a) + (log b).

Exemple :

log 2 ≈ 0,30103

log 6 ≈ 0,77815

la somme des deux logarithmes est 1,07918.

Et on vérifie que log 12 ≈ 1,07918.

De même si "c" est le résultat de la division de "a" par "b", alors (log c) = (log a) - (log b).

Revenons au problème du ministre. On avait :

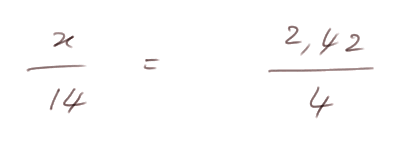
Donc log x - log 14 = log 2,42 - log 4.

log 14 ≈ 1,14613

log 2,42 ≈ 0,38382

et log 4 ≈ 0,60206

D'où log x ≈ 0,92789.

Et, toujours avec sa calculette scientifique, la ministre aurait trouvé que si log x ≈ 0,92789 alors x ≈ 8,47€.

Evidemment, c'est moins précis car on a arrondi les différents logarithmes. Pour le calcul exact, il faut maîtriser la règle de trois :-)

Les logarithmes ont été inventés par l'Ecossais John Napier (écrit aussi Neper), né en 1550 et mort en 1617, pour transformer les grosses multiplications (compliquées) en additions (plus simples).

Note : nous nous moquons gentiment de Xavier Darcos, car c'est toujours rigolo un ministre de l'Education nationale qui ne sait pas compter. Mais il faut dire aussi que X. Darcos est un latiniste distingué qui a écrit un charmant livre intitulé "Dictionnaire amoureux de la Rome antique", et que celui-ci, contrairement à ses capacités en calcul, est tout à son honneur.

Exercices :

Si x est à 7 ce que 52 est à 14, quel est x ?
Arthur a une petite entreprise dont les revenus sont en croissance année après année. L'année dernière, au mois de septembre son chiffre d'affaires pour tout le mois était de 5272 euros. Cette année, au 22 septembre il a déjà gagné 5690 euros sur le mois. Et l'année dernière au 22 septembre il avait gagné 3727 euros sur le mois. Quelle est votre estimation de ce qu'il va gagner cette année pour l'ensemble du mois de septembre ?
Si Marion met ses bras le long du corps, et Jules aussi, lequel des deux aura les mains les plus près du sol, Marion (qui a les bras les plus longs) ou Jules (qui est le plus petit) ?
Calculer 52 783 x 13 475 en passant par une addition de logarithmes.

Réponses

Plan général du cours

Contacter le professeur

Réponses :

x = 26
5272 x (5690 / 3727) ≈ 8049 euros
Jules aura les mains les plus près du sol. Car une autre propriété des figures proportionnelles est que toute paire de distances correspondantes (prises dans chacune des deux figures) donne un rapport constant. En d'autres termes tout est en proportion, y compris la distance entre le sol et les mains de chacun. Le fait que Marion a les bras plus longs ne compense pas ses épaules plus hautes que celles de Jules.
log (52 783) ≈ 4,72249 et log (13 475) ≈ 4,12953.
La somme des deux log est 8,85202.
C'est le logarithme de 711 246 267, 000 186 413...

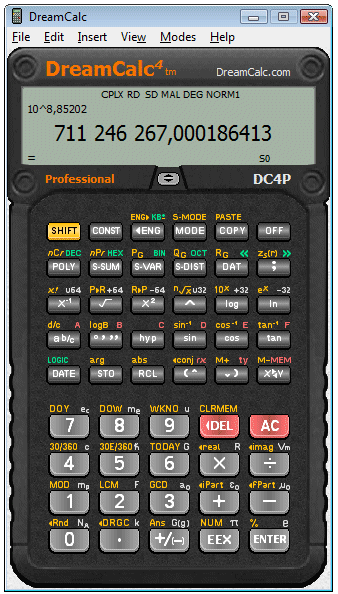
Donc 52 783 x 13 475 est approximativement égal à 711 246 267, car la somme des logarithmes des deux premiers nombres est à peu près le logarithme du troisième.

En fait, la multiplication exacte, qui depuis qu'on a des calculettes est facile à faire, donne 711 250 925. Donc avec les logarithmes, en travaillant avec 6 décimales, on a fait une erreur de seulement 0,000 006... C'est moins que 0,000 01, qui est égal à 1 cent millième.

En Astronomie il y a souvent des très grosses multiplications à faire, et il n'est pas important qu'elles soient parfaitement exactes pourvu qu'elles soient précises à 1/1000 ou 1/10000. Du temps de John Napier, jusqu'au XIXe siècle, et encore au début du XXe siècle, on utilisait les logarithmes pour faire ces calculs.