Advanced financeLesson 8: Commodities and futures markets
Today's topic is forwards and futures (Levinson, chapter 8). The three financial contracts, forwards, futures and options, let time play a special role, but in slightly different ways. (In truth in every financial product, time plays an important role; that's even the definition of a financial product: a contract between two agents, A and B, which specifies flows of cash between them, now and in the future, depending upon various conditions, which may or may not happen in the future.) Forwards are simple contracts signed at time t (today), between two market players, which specify a transaction of something between them to take place at time T, in the future. And the price of the transaction is set at time t (but the transfer of money will take place at T). The price, set at t, of the transaction to take place at T, is called the forward price (or futures price, see below), and is denoted PT(t). The material thing to be exchanged is called the "underlying". It can be, for example, 10 000 bushels of wheat, or a certain number of barrels of oil, or even some financial assets. Futures are forwards calibrated and handled by a stock market, whereas forwards are over-the-counter contracts of a purely private nature between two players. Options are more complicated contracts signed at time t, which give the option (but not the obligation) to the buyer of the contract, to carry out a transaction with the seller. They will be studied in lesson 9. All these contracts have one goal: transfer a risk from the buyer to the seller. That is, reduce a risk that the buyer would naturally encounter in the future, and increase correspondingly that of the buyer.
Forwards Forwards are the simplest of "future contracts". We saw that financial products in general already encompass time in some fundamental way: a financial contract binds a seller to make some payment in the future to the buyer (see lesson 1: "what is a financial product?"). They are distinct from plain transactions at time t (today), after which nothing else has to happen. Forwards are a special type of financial product in the sense that, at time t (today), nothing is exchanged (no tangible value, nor money), only a contract is signed to carry out an exchange at time T, later on. But at time t, the price of the exchange is decided. It is called "the delivery price", and is decided now. For instance, a farmer producing wheat, and a breakfast product manufacturer, may enter into a forward contract in the Spring of 2008, for an exchange to take place in the Fall of 2008 (say October 1st), when the wheat will have been harvested and be ready for delivery.
A forward is a purely private contract between the (future) buyer and the (future) seller. It is not handled by a stock market. With a forward, the farmer and the breakfast manufacturer are assured in the Spring of the price they will apply in the Fall. It is a form of protection against the future. It is also a gamble, in the sense that the farmer will not benefit from a possible increase in the spot price, and the breakfast manufacturer will not benefit from a possible decline in the spot price. (The spot price is, at any date t, the price for immediate delivery.)
Futures are forward contracts calibrated in size, and handled by stock markets.
Grain futures prices Furthermore, margin calls or margin payments, managed by the stock market, are made everyday to both players: if at date t (today), a buyer B and a seller U enter into a future contract whereby at time T (in the future) U will sell some tangible product for the future-price 180€, and the next day (let's call it t+1), the future-price, in the market, has changed to 181€, then, at date t+1, U must pay 1€ to B, and the contract between B and U is modified so that now the agreed upon future selling price is 181€. As a consequence of this, at any time the market value of a future contract is always zero. In other words, no one would pay anything to B to buy from him the contract he holds (binding him to U).
Let's be clear about dates and prices: consider a fixed future date T (say October 1st); at any date t, prior to T, the market specifies a delivery price (which I called, above, the future-price) PT(t) for the exchange to take place at T. This delivery price PT(t) viewed as a function of t, changes every day as t changes.
There exists an important theoretical relationship between the spot price at time t, of a certain quantity of underlying, and the price, specified at time t, in the futures contract for delivery and payment at time T. This relationship holds provided that at any time there are operators in the market that have plenty of the underlying. Notation:
Then the following formula (where "x" stands for "multiplied by") must hold: PT(t) = S(t) x (1 + r)T-t
This formula says that, at time t, the price in a futures contract stipulating delivery and payment at time T must simply be the spot price, at time t, of the underlying multiplied by the risk free factor corresponding to the period T-t. Proof: The idea is to show that any other price than PT(t) at time t would enable someone to make an arbitrage (i.e. earn risk free money). And it requires the assumption that there are operators in the market that have plenty of the underlying at any time. Otherwise the relationship may not hold. Case 1: suppose the price stipulated in the futures contract is F > S(t) x (1 + r)T-t In this case, an operator O can, at time t, borrow the sum of money S(t) and buy right now on the spot market the underlying; and at the same time, O enters, as a seller, into a futures contract with another market player B, which will be a buyer, whereby O promises to deliver to B, at time T, the underlying and receive F from B. At time T, O will deliver the underlying, and receive the sum F. And he will pay back the money borrowed plus interest, namely S(t) x (1 + r)T-t Therefore O will make a risk less profit of F - S(t) x (1 + r)T-t
Case 2: suppose the price stipulated in the futures contract is F < S(t) x (1 + r)T-t In this case, we turn to an operator O' who has plenty of the underlying right now. At time t, O' will enter, as a buyer, into a futures contract with another market player O'', which will be the seller, whereby O' promises to buy from O'', at time T, the underlying and pay F to O''. At the same time t, O' will sell on the spot price, for the price S(t), the same quantity of underlying as in the futures contract, and receive the sum S(t). O' will place this sum at the risk free rate. [Technical comment: The above selling of some of the assets which O' holds, in order to make risk free money with S(t), can rightfully be seen as some reasoning trick. There are alternative tricks like "it is always possible in some markets to sell short", i.e. to receive today, at time t, the spot price for some asset we shall deliver in the future, at time T. But then why would the buyer accept to pay today the spot price and receive the goods only at T? The buyer could himself make money by getting the assets today, and selling them, etc. We shall meet this trick used again and again, in particular when we construct risk free portfolio with a combination of long buying and short selling. We shall meet it when we study "risk neutral probability measures". It is the teacher's opinion that the role of time in ownership ought to be analyzed with a more elaborate theory.] Then, at time T, O' will have S(t) x (1 + r)T-t in cash at the bank. And he must, at that time T, buy the underlying from O'' and pay F for it. So after this operation, after T, O' finds himself with the same quantity of underlying as before and he made a risk less profit S(t) x (1 + r)T-t - F
Because, in finance, markets adjust themselves so that arbitrages (that is risk free profits) do not exist, such cases are impossible. Therefore we must have PT(t) = S(t) x (1 + r)T-t
In a continuous time model, the formula becomes PT(t) = S(t) x er(T-t) where r is the risk free rate in the continuous model.
More practically: In actual markets, the theoretical relationship, for a variety of reasons, may not always be observed. When PT(t) > S(t) x (1 + r)T-t the market is said in contango. When PT(t) > S(t) x (1 + r)T-t the market is said in backwardation.
When the underlying is foreign currencies: Then a slight adaptation of the above reasoning shows that in theory we have PT(t) = S(t) x (1 + r - rf)T-t where rf is the risk free interest rate on the foreign currency.
(from Levinson chapter 8) Futures involve commodities, but also financial products. Why trade futures?
Types of futures contracts
How futures are traded: futures are handled by an exchange (an "exchange" is an organized market, actually run by a firm called "the exchange"). Buyers and sellers actually deal with the exchange, not with one another. The saying goes like this: "the exchange is the buyer of all sellers, and the seller of all buyers." It is possible for a buyer (or a seller) to terminate his contract before the exercise date. It is referred to as liquidation of the initial contracts. Contract terms
Futures exchanges: 35 important exchanges worldwide
* merged with NYSE in 2007, to form the NYSE Euronext Competition, and merger pressures Trading
How prices are set
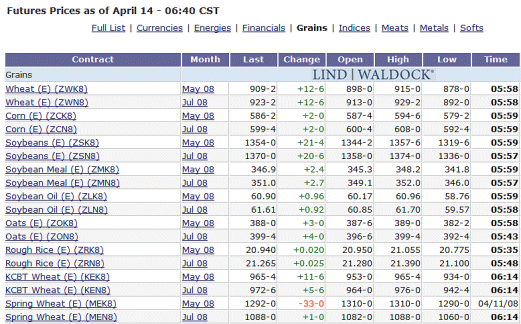
Obtaining price information Commodity futures markets
Reading commodity futures price tables Financial futures markets (adapted - and corrected - from Levinson, pp 187-188) interest-rate futures: trading in interest-rate futures accounts for over 90% of all financial futures trading. The first interest-rate contract, introduced on the Chicago Board of Trade in 1975, allowed financial institutions to hedge the risk that changes in interest rates would alter the value of their portfolios of residential mortgages. The 3-month Eurodollar contract at the Chicago Mercantile Exchange, tied to interest rates on dollar deposits outside the United States, and the Bund contract on Eurex, based on German government bonds yields, now have more than twice the trading volume of any other futures contracts. To understand how interest-rate futures are used, consider the Treasury bond contract on the Chicago Board of Trade. This contract is based on a (30 year) bond with a face value of $100 000 and a nominal interest rate, or coupon, of 8%, and the quoted price is in percentage of face value. In early 1999 such bond was trading at a spot price of about 125, so purchasing a single bond would have cost $125 000. Assume that an investor expected long-term interest rates in September 1999 to be lower than in January of that year. It could have purchased a bond for $125 000 and held it to September, or it could have acquired one bond futures contract for September delivery. In January 1999, the futures price for September delivery was 125.50 and the down payment required was $2700. Now suppose that a fall in interest rates had caused the price of the bond to rise 1%. The bond would be priced (spot) in September at $126 250. An investor who would have bought the bond itself in January would have the following in September: $1250 in capital appreciation + $5333 in interest (8% per year over eight months) = $6583. This for $125 000 blocked for eight months. While an investor, in January, in the futures contract, would have in September: $750 in capital appreciation (126250 - 125500). And this sum would have been received little by little over the eight months, as margin receipts. This for $2700 down payment. Hence in a rising market the investor in interest-rate futures is able to earn a far better return than an investor in the underlying interest-rate-sensitive securities. currency futures stock-index futures share-price futures other financial futures Reading financial futures price tables Clearance and settlement A margin of security: before buying or selling a futures contract, an investor is required to deposit a down-payment, known as a performance bond or initial margin, with the futures commission merchant. The idea is that the investor should always have sufficient margin on deposit to cover potential losses.
Delivery Trading strategies
Measuring performance
Now that we have left bonds four lessons ago (in lesson 4), and studied many other things in the mean time (securitization, int'l bonds, equity, futures), let's take one more look at bonds.
Until 1980, bonds were, as we explained, a "sedate", "boring" financial product. There were issued by governments and some large corporations, that needed to borrow money, and could do it directly without going through banks, because they were very big and safe. And indeed bonds were not very risky. They were less risky than equity. For smaller borrowers, the only way to borrow money was to go through the banking system. A borrower would issue not a bond, but a loan receipt, which would go into the assets of a bank, and the bank would lend the money. The bank (+ the FDIC or some other insurance scheme), also, would protect the depositors. In a sense, the "money supply" in society was totally under the control of the banking system.
With the advent of deregulation and developed computerized financial markets, things changed. Since the 1980's a borrower, even comparatively small, can issue bonds. These bonds will be bought directly by investors in the financial markets. It is (almost) a pure creation of money, since - the reader will remember - money is the receipt of a credit (either from a deposit, or from a loan creation). The banking system is shunted out. In essence, it is a small player B who borrows money from a small player A, and gives A a piece of paper, which is an IOU, and which specifies how A will be refunded. The deregulation has strongly encouraged this kind of risky lending/borrowing, and of many riskier private products of the same nature (asset-backed securities, derivatives, etc.). It is no wonder that this has profoundly modified the financial landscape and made it much more unstable. The explosion of the financial markets, and particularly of the bond markets, should be viewed in parallel with the explosion of the volume of "quasi money". And it is the cause of the present worldwide instability of financial markets. The question is: how to make the world financial markets more stable? Via regulation? Or otherwise?
Consequences of the easiness to issue debt since 1980:
All this suggests that we shall not come back to more stable times with the present system, and that we are living through the end of the present world monetary and financial system. The teacher believes that new entities will begin to offer new private currencies with the feature of being reliable. They will take place outside the regulatory framework of nation-states (a type of social organization responsible for WWI) and decrease their power and importance.
| |||||||||||||||||||||