Advanced finance

Lesson 9: Options and derivatives markets

Introduction

The topic of today's lesson is options.

In the last lesson, we studied forwards and futures. They were contracts, signed at time t (today), specifying a transaction to take place at time T (some date in the future), at a certain price to be applied then, but decided today, which we denoted P_T(t)

Forwards and futures were compulsory contracts, i.e. once signed the two parties were obliged to carry out the transaction as contracted (unless they had agreed in the mean time to cancel it).

Options are different, in the sense that they are only contingent claims. By this we mean that the completion of the transaction will be contingent upon some future event, that is not known today. It is, namely, whether the buyer of the option decides or not to exercise it. And this will depend upon the situation of the market at time T.

The most typical option goes like this:

At time t (today) A enters into a contract with B, whereby A will have the possibility (the option) to buy, at time T, a certain asset from B at a certain price, decided today. The contract is called a "call option". It has a value today, which is normally the price A pays B, at time t, for the option.

The transfer of risk in finance

We would like to take the opportunity of this lesson to make some more general comments about risk in finance, and more specifically about the transfer of risk from one market player to another.

As we said, finance is concerned with risk, in the following sense: sometimes a player A will receive now, at date t, or more generally later, at date T, a sum of money, the value of which "x" is not sure. It will be the outcome of a random variable X.

In order to focus on risk, with time playing no role, let's consider that A will receive, right now, "x", the outcome of X. A does not know what "x" will be. And he may or may not know very much about the characteristics of X.

Suppose that A knows that X has the mean value µ = E(X), and a standard deviation s = std dev (X), and, to make life simple, that X is normally distributed.

A may be able to find another player B who is willing to pay A a fixed sum P right now and accept in exchange the unkown (yet) outcome "x". Of course B must know some things about X in order to be able to make an offer.

The typical situation is that both know "reasonably well", from past outcomes of X, or for some other reasons, µ and s.

Typically B will pay A a price P less than or equal to µ, and "take on the risk" of the security.

In this case A has transfered his risk to B.

Because investors, unlike gamblers, are risk-averse usually B will make an offer P strictly less than µ. The difference µ-P is the "price" paid by A to abandon his risk and receive the sure sum P.

This can be further substantiated with the theory of utility, first developed by Daniel Bernoulli in 1738 with the solution to the Saint-Petersburg paradox.

This was a first example without time, everything taking place "right now".

Now we turn to the more usual situation in finance, when the random variable X will produce an outcome in one year (we are in the simplest discrete time model, with smallest step = one year). In probability theory we say that "waiting one year" is the experiment (see Accounting and Finance lesson 7b for details).

Now the risk born by A concerns an outcome in one year (although time will not play any role here either, but we are in the more usual situation, which may help avoid confusion).

We know that the risk-free securities (namely the short term government bonds) have a price today which is their sure cash flow in one year discounted by the risk free rate.

For risky securities, A, once again, can transfer the risk to B, if he finds a player B willing right now, at time t, to buy the security and receive in one year the unsure sum "x". A will receive right now the price P, and B will receive in one year the sum "x".

Suppose that B has the possibility to buy two securities S and T from players today. To make life simple they both have the same mean value in one year µ, same std dev s, and same price today P.

It looks like if S and T are independent, for B to buy half of S and half of T, would be a good deal. Indeed, let's call V = (S+T)/2, then it is easy to check that E(future value of V) = µ and standard deviation of V = s/1.414... Here is a numerical example, with µ = 100 and s = 19.18 We see that E[(X+Y)/2]= 100 and std dev of [(X+Y)/2] = 13.56

So it looks like B could invest in a portfolio better than S or T alone. And "averaging" like this even more, he could invest in a portfolio with zero risk and the same profitability as S (or T, which is the same).

Here enters the notion of fundamental risk and of specific risk of securities in the market.

According to the CAPM theory, S and T cannot be independent. Otherwise, following the above calculations (which are perfectly correct), B could indeed "average out" his risk to zero. (Follow this link for a review of joint distributions, and examples of random variables which are dependent.)

In the CAPM model, all the securities in the market are linked to a central security M ("the market portfolio") by a beta coefficient, and have on top of that an extra specific risk, that one which can be averaged out. But the market risk cannot.

The formula for the random profitability of any security in the market is

R_S = r_TB + b_S (R_M - r_TB) + e_S

and the expectation and variances of R_S are given by the usual CAPM formulas (see here, bottom of page, for instance).

So we see that "protection against risk" like any other goods can be sold and bought in society. Investor B, who buys the security S from A, and thereby relieves A from the risk presented by S, actually sells to A a "protection against risk", and B's remuneration is the nominal difference between E(X) and P. We saw, however, that most of the times in financial markets, the difference between the Present Value of E(X) and P is zero.

The extraordinary development of derivatives markets over the last 30 years is essentially about these buyings and sellings of risk.

Is it so new?

The business of transfer of risk is not new at all.

Insurance companies do this all the time. Modern ones began in the XVIIth century in London and Amsterdam to insure ship ventures. This is how the Lloyd's started.

The idea of buying a protection agains risk is as old as social life. The simplest illustration goes like this: one thousand persons know that they will incur, every year, a risk to suffer some damage that would cost them say 5000 euros. But the probability of such an accident is 1/1000 for each of them. Several models are possible:

1. every year the accident will happen to one and only one person
2. every year the accident may happen to zero, one or many persons

Model number 2 is more realistic, but anyway, first of all let's see what people can do. They can pay an insurance company 5€ each (plus a little extra fee for operation costs), and the insurance company will insure them, that is will pay for the damages caused by the accident to any one who suffers it. The insurance company receives every year 5000€, and this is also its average cost every year. This way, no one will have to support the brunt of 5000€ of expenses due to the accident. Every one in the community is "protected" against risk.

Of course this model is crude. Actuarial tables enable insurers to make more elaborate models, and run real insurance companies.

Options, generalities

A call option: it is an option contract between A (the buyer) and B (the seller), whereby A acquires today, at time t, the right (but not the obligation) to buy from B, at time T, a certain asset at a certain price.

A put option: it is an option contract between A (the buyer) and B (the seller), whereby A acquires today, at time t, the right (but not the obligation) to sell to B, at time T, a certain asset at a certain price.

There are actually two modes of exercise. And we have mentioned only one, called European option. It is the one that leads to the simplest derivatives and financial calculations. The two types are:

• European option: the option may be exercised only at the expiry date T, of the option, i.e. at a single pre-defined point in time.
• American option: the option on the other hand may be exercised at any time before the expiry date T.

In this lesson, unless otherwise specified, we shall be talking about European options.

Common terms (from Wilmott, chapter 2, Derivatives)

It should be noticed that Wilmott makes forward, futures, and derivatives more complicated than they really are. But his book has the merit of introducing stochastic calculus in a heuristic simple fashion, which makes it easier to follow for the layman than the heavy handed fully mathematical approach.

• premium: it is the sum paid by A to B at time t
• underlying asset: it is the goods or the financial security which is the object of the option. At any time t, we denote its price as S(t)
• strike price or exercise price: it is the price, decided at time t, at which A will buy (in the case of a call) or sell (in the case of a put) the underlying, at time T, from or to B. Usually denoted E.
• expiration date: it is T
• intrinsic value: it is a concept measured at time t. It is the difference (if it is positive) between the current spot price of the underlying at time t and the exercise price: max (S(t) - E). If the difference is negative, the intrinsic value is currently zero. It is not a significant concept.
• time value: irrelevant and vague concept. We shall, however, see the important curve, for a given time t, of the value of an option as a function of the spot value of the underlying.
• in the money: said, at any time t, of an option with a current positive intrinsic value.
• out of the money: the contrary of "in the money".
• long position (in some asset): said, at time t, of the position of a player who owns now, or has the option of buying in the future, at time T, some asset.
• short position (in some asset): said, at time t, of the position of a player who entered a contract whereby he may have to sell in the future, at time T, some asset (in which case he may have to buy them, before selling them, because he does not have them).

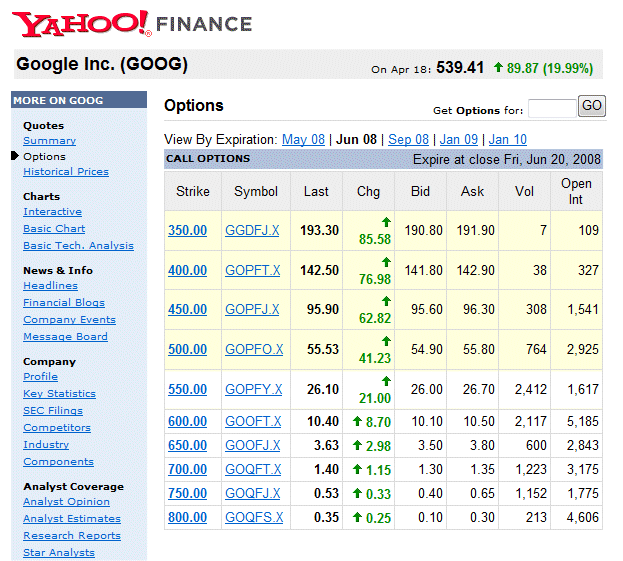
The value of an option:

Let's concentrate, for the moment, on a call option. Suppose that t (now) is the 18th of April 2008, and T is the 20th of June 2008. Here are data given by Yahoo finance on call options on Google:

The spot price of the underlying, on April 18th, 2008, is $539,41

The table (extracted from Yahoo's site) gives the value of a collection of call options, all of them for exercise date the end of June 2008 (T = 20th of June 2008), and different exercise prices.

We see the obvious fact that, the lower is the exercise price the higher is the value of the option today.

• If I want to buy from someone today the right to buy Google at $350 on the 20th of June, the premium I have to pay today is $193.30
• If I want to buy from someone today the right to buy Google at $800 on the 20th of June, the premium I have to pay today is 35 cents.

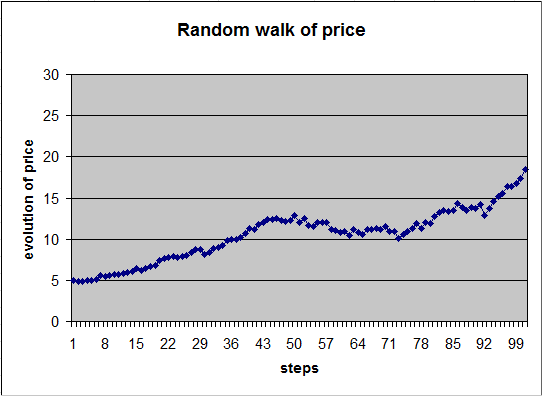
These prices are set by the market, and are presumably in line with the theoretical values of the options as can be calculated using probability theory. (This is what financial analysts, in the mathematical finance dept of banks, spend their time checking, with the help of computers, on slightly more complicated products, involving buying and selling several options and the same time. When they see a significant discrepancy and they are sure of their models, they go ahead and recommend their bank to make what they think is a pure arbitrage: buying today for $80 something really worth today $90. Sometimes, their bank let them play themselves with a certain amount of money.)

Suppose I bought today the option named "GOPFO.X" (the one with exercise price $500, and exercise date 20th of June). We notice that the option today is "in the money", in the sense that if I could exercise it today, I would earn $539.41 - $500 = $39.41 We also notice that I must pay $55.53 to acquire it today. And its value is going up. But this is of little importance. What matters is whether the option will be "in the money" the 20th of June, and how much will I make with it.

The theoretical calculations go like this: the evolution of the spot price of Google from t (now) until T (the 20th of June) will be random (as viewed from today).

At exercise date (20th of June), the option will bring me value if and only if the spot price then is higher than my exercise price of $500.

The question is: what is the probability that the spot price then be more than $500? And, more to the point, what is the average value my option will bring me then? And finally, how much should I pay for it today at time t (18th of April)?

The average value of the option at time T can be computed like this:

Average value of option at T =

   $0 x Pr { spot price at T < $500 }
+ $1 x Pr { spot price at T = $501 }
+ $2 x Pr { spot price at T = $502 }
+ $3 x Pr { spot price at T = $503 }
+ $4 x Pr { spot price at T = $504 }
+ $5 x Pr { spot price at T = $505 }
+ etc.

If we can compute all these elements, we can compute the average value of our option at time T. It is an approximation, because we should use continuous probabilities. We can also use Monte-Carlo methods (i.e. simulations using Excel or any other simulation software).

It turns out probability theory can compute exactly the average value of the option at time T. The path of the spot price from t to T is called a random walk of a geometric nature. Once we know its "drift" and its "volatility", it is a reasonably simple calculation in the theory of random walks.

It is important to notice, though, that the fact that probability theory is able to compute exactly, with a "closed analytical formula" the above expectation, is not fundamental in itself. Simulations can do it too, and with any precision we like. And simulations are much more powerful than analysis in the sense that they can compute all sorts of things outside the reach of analysis. Analysis, however, sometimes gives insights into phenomena that simulations do not give, at least not in the same way. Students should develop a clear view of what is the toolbox called classical mathematics, when it is useful and when it is not. And they should not attach too much importance to mathematics, in particular to mathematical virtuosity, which too often is displayed by scholarly dolts who would not survive five minutes in an unfamiliar environment.

Here is an example of random walk (generated with the following Excel document). It is "discrete", the time step is 1 (think, for instance, of 1 day), the evolution from one step to the next is a multiplicative factor normally distributed with mean 1% (it is the "drift") and standard deviation 3% (it is the "volatility") :

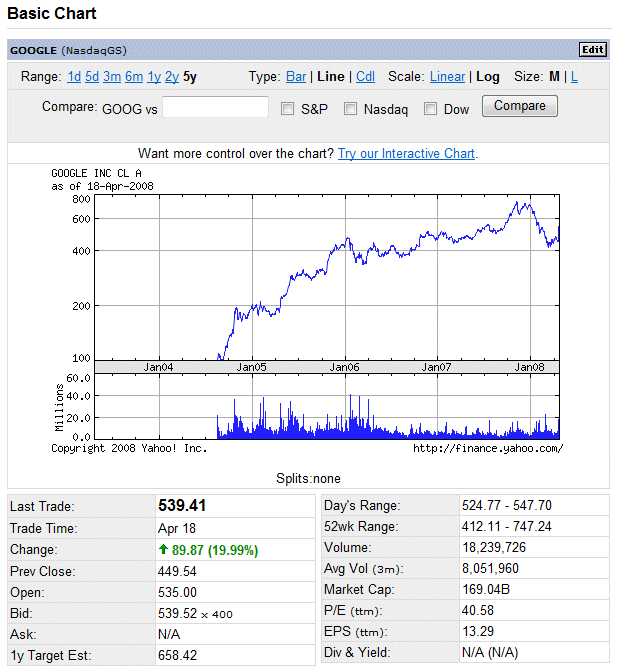
We shall see the exact formula to compute the average value of my option, at time T, and also the price I should accept to pay for it today, at time t, later in the lesson. For the time being let's notice that we need to have an idea of the drift and of the volatility of Google's spot price. Such values are not given in any theoretical tables. We must estimate them. To help us we have the past history of Google spot price:

With these data, and more detailed figures, published by all the good stock market journals and sites, we must construct our own model of what will be the behaviour of Google spot price in the next two months.

Put-call parity

The main theoretical problem concerning options is the computation of the price C(t), today, at time t, we should pay for a call option of exercise date T and strike price E. Similarly for a put option and its price P(t).

We shall wait a bit more before solving the problem entirely, but let's make some progress. S(t) will represent the price of the underlying at any time t.

At time T, the value of a call option is simple to figure out:

C(T) = max( S(T) - E, 0 )

Indeed, if S(T) is higher than E, the option is "in the money". We can exercise our option and buy the underlying from the other party who sold the option to us. Since the price we get is E, and is less than the spot price S(T), we make, at time T, a profit S(T) - E. On the other hand, if at time T, the option is out of the money, its value is zero.

Similarly, the price of a put option P(t), is easy to figure out when t = T

P(T) = max( E - S(T), 0 )

There is a nice and simple relationship between the price, at time t (now), of a call option and the price of a put option with the same exercise date T, and same strike price E. And it involves in a simple and important way the principle of no arbitrage in finance. This principle says: "Two identical financial products (in terms of future randomness) must have the same price today."

Let's look at a portfolio, at time t, made of a call option that we just bought, and a put option that we just sold, both with expiry date T and strike price E.

The value today at time t is C(t) - P(t)

And the value at time T is C(T) - P(T) = max( S(T) - E, 0 ) - max( E - S(T), 0 ) = S(T) - E

Now comes the astute observation. There is another portfolio, that we can construct at time t, and which will have exactly the same random value at time T. We just have to buy S at time t, and also borrow a sum of money that will just have the value E at time T. This second part is Ee^{-r(T - t)}. Indeed, if I borrow Ee^{-r(T - t)} at time t, then at time T, my debt will be E.

This alternative portfolio, at time t, costs S(t) - Ee^{-r(T - t)} and will have, at time T, the value S(T) - E.

According to the no-arbitrage principle, it must have the same value at the first one. Therefore

C(t) - P(t) = S(t) - Ee^{-r(T - t)}

This is an important relationship, linking at time t, the price of the call and put options, of the underlying and the risk free rate r.

Options give leverage to bets

The next three sections are adapted from Ross, Westerfield and Jordan, Fondamentals of Corporate Finance, Sixth edition, Standard edition, McGraw-Hill Irwin, 2003, chapter 14.

Suppose we have $30 000 to invest either in AOL shares, the spot price of which today is $32.28, or in AOL call options to expire at the end of next January (say, we are in September), with exercise price $30, their price is $6.

In the first case we buy 929.37 shares, because 30 000 / 32.38 = 929.37

In the second case we buy 50 call contracts (a contract is for 100 simple options), because one contract is worth $600, so we can buy 50 of those.

Pricing of simple options

We shall use again the following very important and powerful idea:

if two securities or portfolios of securities have exactly the same random behavior and values at date T, they must have the same price today (at t).

otherwise there would exist an arbitrage possibility.

This powerful idea will be applied in an astute way to compute the price today of a simple call option.

Consider a share with spot price $100. We look at a call option, exercise date T = t + one year, exercise price $105. The risk-free rate (which will happen to play a role) is 20% per year.

Case I: the probability model for the share is such that the option will always end up in the money. The share can end up at either $110 or $130. Then the value of the option is either $5 or $25.

Notice that if we invest $105/(1 + 20%) = $87.5 today, we shall have for sure $105 at T.

Therefore, if today we invest into a portfolio made of $87.5 in risk-free asset + C in one option, this portfolio will have the values $110 or $130 in one year, and behave exactly like the share.

Therefore it must have the same value today.

So S (the value today of the share) = C + $87.5.

Or equivalently, C = S - $87.5 = $12.5

Case II: The share can end up at either $110 or $130. But the value of the share today is $120. Then the value of the option is either $0 or $10.

In that case, in order to replicate S itself at T, invest into 110/1.2 + two options.

Then C = $4.17

Notice that, in either case, the probabilities driving the values of S at T do not enter the equations.

In case II, we used two options because, at T, one option in the favorable case was worth half the difference between 130 and 110. More generally, we would use the ratio [Delta values of S at T / Delta values of C at T]

Equity as a call option on the firm's assets

Surprisingly enough, equity in a firm functions exactly like a call option on the firm's assets.

See Ross, Westerfield and Jordan, "Fundamental of Corporate Finance", McGraw-Hill Irwin, Sixth Edition, 2003, pp 468-469

More generally speaking, many investments in life can be analyzed as options.

The binomial model

from Paul Wilmott, Introduces Quantitative Finance, John Wiley & Sons, 2001, chapter 5

in progress

go to sounds to listen to the lectures

Brownian motion

in progress

Introduction to stochastic calculus

in progress

Black & Scholes formula

in progress

Documents: