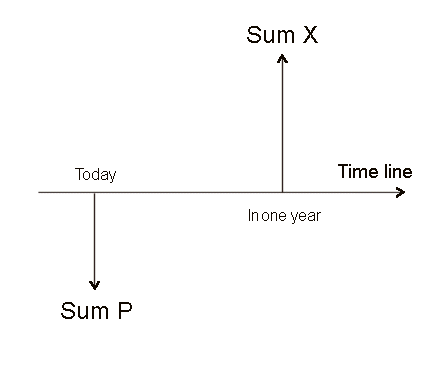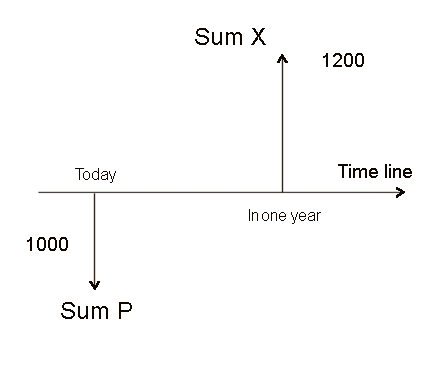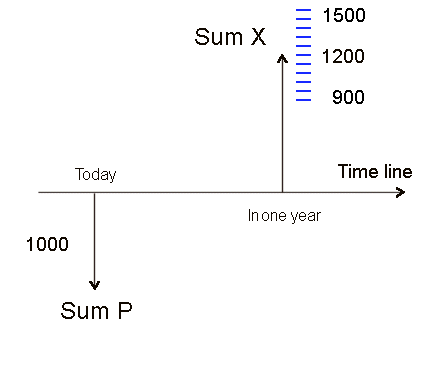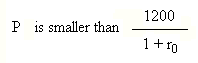Finance with a review of accountingInvestments |
|||
|
|
|
||
| Introduction Investments An investment is a transaction today Creation of value for ourselves The modelling of time Right and wrong reasoning When the future sum X is sure When future the sum X is risky Summary One of the first modern problems of probabilities Why investors are risk averse |
|||
|
Our review of accounting, general accounting and cost accounting, in order to prepare our understanding of finance, is now complete. We are ready to study investments, the main economic concept Finance is concerned with. In order to study investments, today we introduce one of the fundamental mathematical tools of Finance: simple probability theory and random variables. Modelling of risk An endless source of confusion The effortless creation of promissory value, and the problems it causes First of all, let's start with a description of what are investments, made with real value or with money.
The purpose of finance is to study investments: how to select good investments, and how to get the money to pay for them. The second part, "how to get the money to pay for them" (that is "how to finance investments"), we shall leave for later lectures in this course. During the first few lectures, we shall focus our study on which investments are good ones.
What is an investment? In other words, it can be viewed as the opposite to consumption. If, during a period [t1, t2], I consume all the value I produce (from my work or otherwise) like the cicada from the fable of La Fontaine "The Cicada and the Ant", I save nothing, I invest nothing. If, on the contrary, I produce Q, but consume only C, and C is less than Q (with some appropriate unit of measurement), then S = Q - C is what I save, or equivalently what I "invest". I intend to consume S, or, better, to consume whatever S will be able to produce, in the future. The latter case is the most customary definition of an investment: we set aside some value, and we make this value work, we don't just wait to consume it later. Monetary investments We hope to reap more than we invested. The common concept of investment encompasses several concepts:
It is because of this last concept of risk that we shall use elementary probability theory to model and study investments. Two types of investments: physical, and financial
In the former case we are the main entrepreneur. In the latter case, we only buy stocks, or bonds, but the entrepreneur is usually somebody else; we only have some financial contract with him. The case where we buy apartments to rent them is closer to a financial investment than to a physical one. Indeed, there is usually no interference between our proprietary know-how and the running of a flat-rental activity. One must also note that often, investing into flats for rent is primarily a speculative investment expecting (from urbanistic considerations) capital gains or at least value protection. Anyway, for what we want to study today,
the two types of investments, physical and financial, make no difference. Standard graphical representation One year
If the investment will produce cash flows over several years, the representation is this: Several years
An investment is a transaction today It is important to pay attention to this point: an investment is a transaction
today As you see, we shall mostly use the implicit description of financial investments, but all the considerations of today's lecture apply undistinctively to physical and financial investments. A contract A link between the present and the future More complicated contracts A security. Its value today The case of a physical investment Personal values [this item
can be skipped]
The question of "what is the value of S, today, for us?" is a central question of finance. Yet, in this course, we shall not dig into the subtle subject of personal value, and we shall stick to the standard approach. For us the personal value of something is the amount of money we are willing to pay for it. In other words, we shall equate personal value for an agent and the money an agent pays for the concerned object. The above considerations glide over the various deep questions raised by the standard theory of money: for instance in a financial contract, the value of what we buy is the value of the money we give. But money looses value (and this has nothing to do with inflation!) in the sense that it doesn't produce value, whereas bonds do - but only if we trust that the sovereign authorities will not change the interest rates... And bonds are not money, although it is likely that in the future they will be more and more money-like. The theory of money is in need of an overhaul as sweeping as the theory of relativity. What makes finance fun: immediate creation of value In our view, Modern Financial Theory has failed Yet we need to understand simple probabilistic
techniques
Creation of value for ourselves: Comparison between the money we pay or spend today, and the value for us today of the stream of future cash flows we are buying
This is the reason why, perhaps surprisingly, it is only in physical investments that we can create value, more or less for sure (technically, with a positive expectation), while in financial investments the theory, as it goes (that is the Modern Financial Theory, or MFT), says that what we buy we pay exactly its value for, therefore we don't create any value for ourselves. We may only make money from fluke. Modern Financial Theory This theory is powerful, but also has limitations. It doesn't explain well phenomena like bubbles, day-trading, the success of superinvestors like Buffett and others from the "Graham school"; etc.
In daily life, as well as in Physics, time is represented as a continuous parameter, although in advanced Physics, it is a debatable question. After all energy was represented by Planck on a discrete scale. At first, that was just in his equations, because he needed that to solve the ultraviolet catastrophe riddle! Yet, it became reality as far as we can talk meaningfully of it. But for the sake of simplicity, in Finance, we shall first of all represent it as discrete. The calculations and reasoning, at first, will be simpler. Therefore, there will be the dates: today, in one year, in two years, etc. Also, as a consequence, the shortest time duration will be "one year".
Right and wrong reasoning in finance: Do not compare values of things at different times In Finance we always compare two values at the same time, usually today. Vague sentences Similarly, in a paragraph below, we shall compare a value of 1000 euros today, to 1200 euros in one year. What is really meant by this is: how does 1000 euros today compare to the promise, today, to receive 1200 euros in one year. If we can exchange one for the other, is it a good deal? We shall see that it depends... Deep misunderstandings Finance, like accounting, is full of misunderstandings. A beautiful one, seen everyday on TV, is when anchormen or anchorwomen say sententiously "the bank so and so is strong because it has a high level of capital (in French "fonds propres")". Most TV watchers, as well as the speakers, picture the "fonds propres" on the asset side of the balance sheet of banks, and think "well, if they have a lot of "fonds propres", they will be able to withstand a run, so there is no risk for my deposits". Such a view of banks, which is very common, and stems from the age-old perception of money as precious metal or tangible value, is profoundly mistaken.
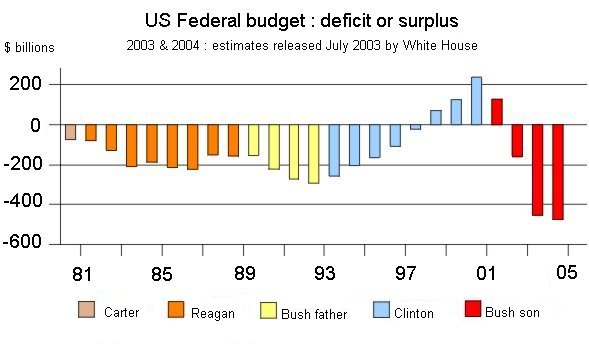
(Let's go back to investments with a payoff in one year.) Usually - we all know that - the future is not sure. If we invest a sum P today into buying a security S, or - equivalently - into setting up a project, the cash flow X that S will produce in one year is not a sure figure. There is one special case where X is a sure figure (or a figure as sure as possible in the world we live in): it is when we lend money, for a short period of time (a few days up to one year), to the government of a large economically well developed nation. The typical example is the United States. Over the last twenty years, at least, the US government has run budget deficits, and therefore has become a large borrower.
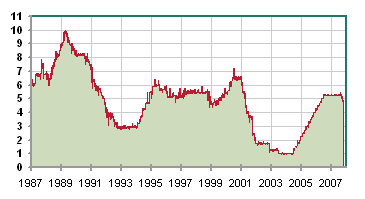
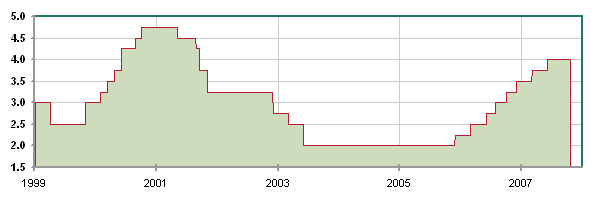
It borrows by selling short term Treasury Bonds in dollars. And, when they mature (when the time comes to pay them back, after one year), it borrows new bonds to pay for the old ones, and their interest, plus the new deficit.... The current US public debt is of the order of $8000 billion. This debt is made of many kinds of bonds, a large part of them are short term bonds. A part of this debt is held by foreigners (between 1/4 and 1/3, figure to be checked). Here is a list of foreign governments holding US Treasury Bonds: US Bond Holders. See also article on China exports. The interest rates on the bond markets, for the various types of bonds, result from supply and demand of money, between lenders and borrowers, and from risk appreciation. But for very short term (a few hours) bonds, the rates are fixed by the central banks managing each currency. In Europe, the central bank managing the euro is the European Central Bank (ECB), located in Frankfurt. In the US, the central bank, created in 1913, is the Federal Reserve System (the Fed). It manages the dollar; for instance, it adjusts the quantity of dollars in the US economy according to some economic objectives; and it decides the very short term rate. To simplify the exposition of the concepts, let's consider the very short rate corresponds to the one year rate. It is denoted r0. At the moment (late October 2007), the short term rate in the US is r0 = 4,75%. That is, you can lend $1000 dollars to the US government; you receive today a TB (Treasury Bond); and, in one year, the US government will take back (or just cancel) your TB and give you $1047,5. It is as simple as that. And it is "sure" - at least as sure as what sure means. Four years ago, the short term rate in the US was 1% (see article). But, since the US gov borrows a lot, it must keep its TB attractive, so it jacked up the rate. The Fed also does this to keep inflation at bay in the US. These are vast questions that we shall study step by step. US risk free rate
In the euro zone, lending and borrowing take place (mostly) in euros. The short term rate r0 of the ECB (European Central Bank), in late October 2007, is 4%. If you lend to one of the governments of the euro zone 1000 € for one year, in one year you will receive 1040 €. Euro risk free rate
For further discussions, see article. From now on, we shall become a more theoretical, and consider an economic space with one currency, and no longer think of the dollar zone, or the euro zone, or the yen zone etc. The rate r0 is called the risk-free rate (it is different in different currency zones). If we lend money to a risk free borrower, we get the risk free rate. Therefore, lending today a sum P, we will get, in one year, a sum X = P x (1 + r0)
When the future sum X is risky When the future sum X is not sure, we say it is risky. That is, the actual sum we shall get in one year will be one value out of a collection of possible values. For instance, if you buy today one Google stock, pay a price P = $670 (it was $312 two years ago) , and sell your stock in one year; in one year, you will get a value that may be $700, or $800, but also may be $600, or $500, etc. It is not sure. The same is true with a physical investment: you invest today a sum P into a physical investment, expecting a cash flow in one year (or, more realistically, a stream of cash flows over the next few years); you don't know what exactly these cash flows will be. Physical investments are never risk-free. Let's look at a simple investment of 1000. Suppose, to start with, that the payoff in one year is 1200, for sure:
Great ! This a sure investment with a profitability of 20%. It's only a classroom example, unfortunately. At present the risk-free rates, in all the strong currencies of the world, are less than 5%. Suppose, now, instead of receiving for sure 1200 in one year, we will receive a sum X that may be 1200, but may be more, and may also be less. 1200 is only a "middle value". In a short while, we shall put a more precise concept on this idea of middle value. We could represent the investment as this:
To represent risk in finance, we use simple probability theory and in particular the concept of random variable (abbreviation: RV). We say that the payoff X which we shall receive in one year is a random variable which will take an actual value (it is called "an outcome") out of a possible range of values. When a security S promises a future payment X which is risky, with a "middle value" of, say, 1200, if we are offered to buy S today for a price P, we will require that the profitability of our purchase be more than r0, the profitability of risk-free securities. The price P, which we will accept to pay, is such that
or, equivalently,
Suppose, we are in an economic area where r0 = 5%. Then 1000 invested today in a risk free security would yield, in one year, 1050. Conversely, a risk free security, paying 1200 in one year, would cost today P = 1200 / (1 + 5%) = 1142,86 Check: P = 1142,86, and X in one year = 1200; the profitability is (1200 - 1142,86) / 1142,86 = 5% But the point is that if X is no longer sure, but risky, then we won't accept to pay P = 1142,86 for the security S, we will pay less. This is a consequence of the fact that normal finance people are risk-averse. What we will pay depends upon the riskiness of X. The more risky, the more "average profitability" we want, and therefore the lower the price today. For instance, if the riskiness of X leads us to require a profitability of 30% (computed with the "middle value" of X), then we will only pay P = 1200 / (1 + 30%) = 923 Who are risky borrowers?
Most countries, in their history, defaulted on their debt at one point or another. In modern history (after 1453), the first country to have defaulted is Philippe II of Spain in the late XVIth century. Various states of the US defaulted in the XIXth century. Argentina defaulted numerous times. Mexico defaulted in 1982, and again in 1994, etc. And, as we saw, physical projects are always risky, some of them moderately, some of them very much. For a large corporation, well established in a market which is growing, to make an investment to increase capacity to adapt to the growing market is moderately risky. On the other hand, an investment to set up a new firm which will use a new technological process, or serve a new market, or produce a radically new type of product, is usually a highly risky project. How do we measure risk? Answer: the risk of a security will be measured by the spread of the variability of the profitability of its payoff compared to its "middle value". To formalize all these ideas more precisely, we need probability theory (for instance, what we introduced informally as "the middle value" of a risky sum will become the expectation of a random variable). So now we turn to the study of simple probability theory. Randomness is something we are all very familiar with, but it took about three centuries, from the first correct descriptions by Pierre de Fermat and Blaise Pascal in the mid XVIIth century, to put it on really clear grounds. It was done only around 1930 by the great Russian mathematician Andrei Kolmogorov (1903-1987).
The value today of a "security" S promising a sum of money X at a date t in the future (today being 0), depends upon three parameters: 1) obviously, the value X (in certain circumstances it is called the face value), 2) the time duration t 3) and the risk (or creditworthiness) of the signatory
We shall use the theory of probabilities to model risk.
One of the first modern problems of probabilities One of the first modern problems of probabilities was posed, but not solved, by Luca Pacioli, in his book Summa written at the end of the XVth century. It referred to a game called balla between two players, which was essentially equivalent to tossing a coin, whose winner would receive the two equal stakes. The problem goes like this: A and B are playing a fair game of balla. They agree to continue until one has won six rounds. The game, for some reason, has to be stopped when A has won five and B three. How should the stakes be divided? (source: Peter L. Bernstein, Against the Gods, p 43) Another famous person who spurred the development of modern probabilistic ideas by Pascal and Fermat was Chevalier de Méré, in the XVIIth century: he had notice from a long experience of playing dice that in series of twenty four throws of a pair of dice, the double-six would come up (in at least one of the twenty four throws) about half of the times. He wanted to know why and how to explain it.
Here is an illustration with a small example: suppose we have the choice between two offers
Daniel Bernoulli in the early XVIIth century introduced the notion of utility. He explained that the extra 10 euros from 200 to 210 have a smaller utility to most people than the 10 euros from 190 to 200. (In other words, the curve of utility as a function of money is increasing but concave, like for instance the function x -> square root of x.) In that case it can be shown that the utility of offer 1 is higher than the utility of offer 2. (It uses the notion of expectation, introduced in the second part of the lecture.) So investors prefer offer 1 which has less uncertainty.
Break time |
|||