Exemple de notations kabbalistiques en mathématiques qu'il vaut mieux éviter
Contenu:
-- Construction du plan projectif
-- Utilité
-- Remarque
-- Exemple d'application : le théorème de Pappus
Construction du plan projectif
Ce "plan projectif" qui est un concept effectivement très important en géométrie, et que l'auteur du livre dont l'image ci-dessus est extraite désigne par
ℝP2 = { ℝ3 \ (0, 0, 0) } / ~
est en réalité construit comme ceci :
On se place dans l'espace ordinaire à trois dimensions, et on considère d'une part un point donné, par exemple l'origine, et d'autre part un plan qui ne passe pas par l'origine, par exemple le plan horizontal P défini par z=1.
On considère toutes les droites qui passent par l'origine. Elles forment un faisceau rayonnant à partir de (0, 0, 0). Toutes les droites du faisceau coupent le plan P, sauf celles dans le plan horizontal z=0.
On associe toutes les droites du faisceau qui coupent le plan P à leur point d'intersection avec P. Et on dit que les autres droites correspondent à des "points à l'infini" qui complètent le plan P. On note ce plan complété par le signe P*.
Noter qu'une direction donnée dans P* et celle obtenue en faisant un demi-tour de 180° correspondent au même point à l'infini.
Le plan P plus ses points à l'infini, dénoté donc P*, porte le nom de plan projectif.
Utilité
Avec cette construction astucieuse, il y a maintenant une correspondance biunivoque entre les droites du faisceau et les points du plan projectif P*.
Pourquoi passer par cette construction, avec un faisceau de droites issues de l'origine, pour décrire le plan projectif P*? Réponse: parce que maintenant à chaque point de P* correspond une droite du faisceau. Mais dans le plan P* tous les points n'ont pas la même nature: certains sont "ordinaires" d'autres sont "à l'infini". Tandis que dans le faisceau, toutes les droites ont la même nature.
En outre, en géométrie projective, on est souvent amené à opérer une projection centrale d'un plan vers un autre non parallèle. Alors des points qui sont à l'infini sur l'un ne le sont généralement plus sur l'autre. Donc traiter tous les points (ordinaires ou à l'infini) à la même enseigne est commode. C'est ce qu'effectue la bijection entre les points de P* et les droites du faisceau de droites issues de (0, 0, 0).
Autrement dit, pour raisonner sur la géométrie de P*, on peut raisonner sur la géométrie du faisceau dans R3. Et cela clarifie et simplifie souvent les choses.
Les droites de P* correspondent aux plans dans l'espace 3D passant par (0, 0, 0). Tous les plans coupent P de manière habituelle, l'intersection étant une droite ordinaire, sauf un plan -- celui horizontal -- qui ne coupe pas P, mais dont l'intersection avec P* est la droite à l'infini de P*.
Maintenant, par exemple, dans P*, deux droites se coupent toujours. Soit elles ne sont pas parallèles et elles ont une intersection ordinaire, soit elles sont parallèles et elles se coupent en un point à l'infini.
Remarque
À notre sens { ℝ3 \ (0, 0, 0) } / ~ est une "notation kabbalistique" qui n'ajoute rien et qui dissimule des notions géométriques astucieuses mais élémentaires.
De toute façon, on ne fera pas l'économie d'une explication. La plus claire et géométrique elle sera, le mieux ce sera.
Ensuite la notation P* fait parfaitement l'affaire.
On ne trouvera jamais de notation comme { ℝ3 \ (0, 0, 0) } / ~ dans l'ouvrage d'Alexandrov, Kolmogorov et Lavrentiev. Ils présentent la géométrie projective dans le chapitre III, section III.13, du volume 1. Leur présentation est géométrique et très simple. Puis ils montrent quelques résultats non intuitifs, puissants et utiles de géométrie projective. L'énergie intellectuelle du lecteur ou de la lectrice n'est pas réquisitionnée pour avancer au coupe-coupe dans des banalités en notations kabbalistiques, mais est sollicitée pour comprendre des choses non évidentes, utiles et expliquées aussi simplement que possible.
Il y a bien pire en matière de notations hiéroglyphiques dissimulant des évidences -- ou alors des notions casse-tête, mais appliquant le principe de Jean Dutourd : "C'est à son goût pour les exactitudes inutiles qu'on reconnaît le crétin."
Exemple d'application : le théorème de Pappus
Pappus était un mathématicien grec de l'école tardive d'Alexandrie qui vécut au IVe siècle après jc. Il est célèbre pour avoir démontré le théorème suivant : dans un plan on considère deux droites quelconques (sécantes ou parallèles)
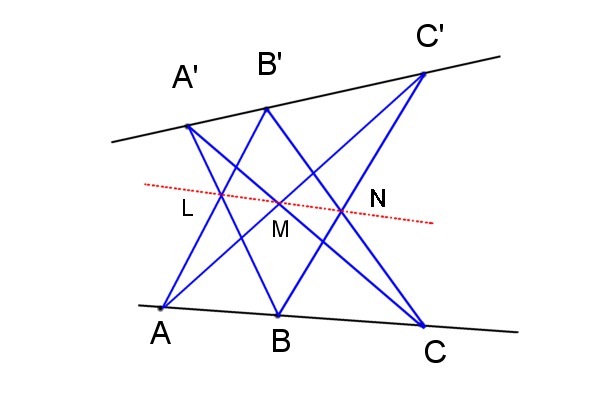
sur la première on note trois points quelconques A, B, C. Et sur la deuxième trois points quelconques A', B', C'.
Alors les points L, M, N, construits comme montré sur la figure, sont toujours alignés.
Le théorème de Pappus appartient à la géométrie projective. Un résultat important, élémentaire à démontrer, est que si on a deux plans projectifs P* et Q* et un point C en dehors d'eux, alors on peut projeter tous les points du premier sur le second, en traçant des droites passant par C: on appelle cela une projection centrale, et des droites de P* restent des droites de Q*.
Utilisons cela pour démontrer Pappus (schéma de la démonstration). On va utiliser maintenant la notion de longueur dans un espace euclidien, ce qui n'était pas le cas plus haut, car la géométrie projective n'utilise pas la notion de longueur.
Projetons la droite des points A', B', C' à l'infini.
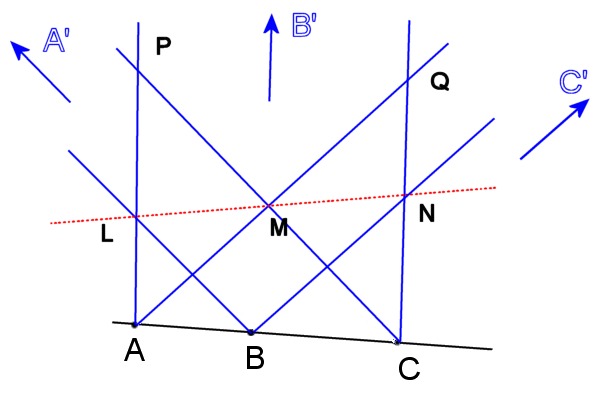
A' est projeté à l'infini, donc les droites BA' et CA' sont maintenant parallèles. Idem pour les deux autres paires.
Regardons la figure ci-dessus, et appliquons le théorème de Thalès :
Maintenant l'alignement de L, M et N est évident, car par Thalès on a PL/PA = CB/CA = CN/CQ.
Et une projection d'un plan sur un autre transformant seulement les droites en droites, ils étaient forcément alignés dans la première figure.
PS1 Le théorème de Pappus, ainsi que celui de Desargues, jouent un rôle fondamental dans une approche plus abstraite et générale de la géométrie. Voir le livre de Laurent Lafforgue, Géométrie plane et algèbre, Hermann, 2018.
Présentation du livre : Cet ouvrage issu d'un cours donné à l'École professorale de Paris (EPP) a pour objectif de présenter l'équivalence entre la théorie géométrique des plans affines ou euclidiens et la théorie algébrique des corps et de leurs équations linéaires ou quadratiques. Ces résultats permettent d'étudier les problèmes de constructibilité à la règle et au compas, et d'en donner une solution générale permise par une seconde traduction géométrique des équations algébriques qui n'est autre que la théorie de Galois. Celle-ci est présentée de deux manières différentes : la manière classique et sa réinterprétation par Grothendieck. Ce texte est précédé d'un exposé général de la notion de théorie et de celle de modèles d'une théorie, qui formalisent la distinction entre syntaxe et sémantique, entre formalisme logique et contenu mathématique.
Dans cette "école" L. Lafforgue a aussi donné un cours sur la théorie des catégories :
INTRODUCTION AUX CATÉGORIES par Laurent LAFFORGUE, Ancien élève de l’ENS Ulm, agrégé de mathématiques, Médaille Fields. La notion de catégorie permet de penser de manière unifiée un grand nombre de constructions mathématiques familières, y compris parmi les plus simples. Apparue il y a à peine 80 ans, elle a également permis d'incarner dans une théorie mathématique propre l'idée générale que les objets mathématiques doivent être envisagés dans leurs relations mutuelles. D'apparence presque trop facile et élémentaire au premier abord, bien que générale et abstraite, elle s'est avérée étonnamment féconde, permettant de repenser à nouveaux frais et de renouveler des pans entiers des mathématiques. Elle fournit en particulier le cadre le plus naturel où s'opère l'articulation de la logique et des mathématiques, c'est-à-dire des théories formalisées vues comme des langues et de ce qu'elles permettent d'exprimer.
I. Catégories : exemples familiers, définition, constructions dans les catégories par limites et colimites.
II. Foncteurs : définition, exemples, catégories de foncteurs, préfaisceaux, lemme de Yoneda, faisceaux.
III. La notion de paire de foncteurs adjoints : définition et exemples.
IV. La notion d'équivalence de catégories. Exemples familiers. Application à la théorie de Galois et à celle du groupe de Poincaré.
V. Logique catégorique.
On espère qu'il en fera aussi un livre, car il est très difficile de trouver de bons livres introduisant à la théorie des catégories. Il en existe bcp, mais soit ils sont simplistes à l'extrême, soit ils sont trop élevés dès le départ.
PS2 En topologie avancée, on apprend que le plan projectif est une surface fermée sans bord, un peu comme la surface d'une sphère, mais à un seul côté !