Cours de mathématiques de 2e

Statistiques : histogrammes

Texte

Un histogramme est une façon de représenter des données statistiques.

Par exemple, supposons que dans une classe de 30 élèves je note l'âge de chaque élève : cela fait une "série statistique" de 30 données.

Comment avoir une vue synthétique de la distribution des âges ?

L'idée est très simple : compter combien il y a d'élèves par tranche d'âge, et représenter ces comptes.

Compte par tranches. Evidemment on a le choix sur les tranches d'âge (largeur et bornes). Prenons par exemple des tranches de 6 mois :

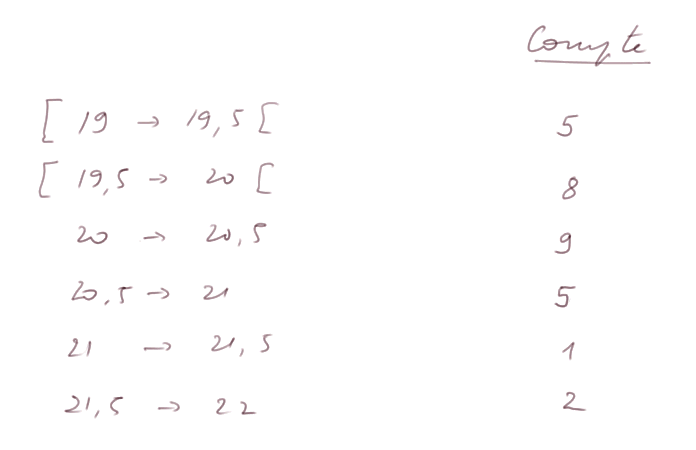
Histogramme. Voici l'histogramme des 30 données d'âge, avec les six tranches qu'on a choisies

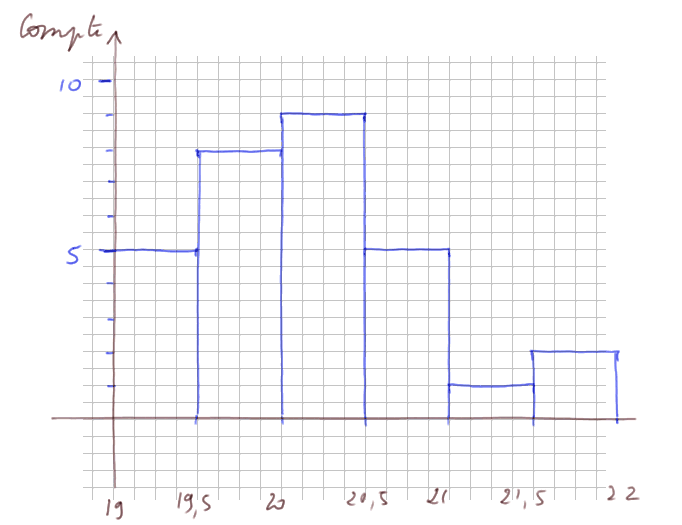
Noter qu'on ne donne même pas les 30 données d'âge, l'histogramme ne présente qu'une vue synthétique.

Deuxième exemple : Soit les 30 données ci-dessous, issues d'une origine quelconque (expérience, sondage, mesures dans un groupe, etc.)

Représentation naïve : le graphe des données elles-mêmes. Voici les 30 données représentées sur un graphe l'une après l'autre

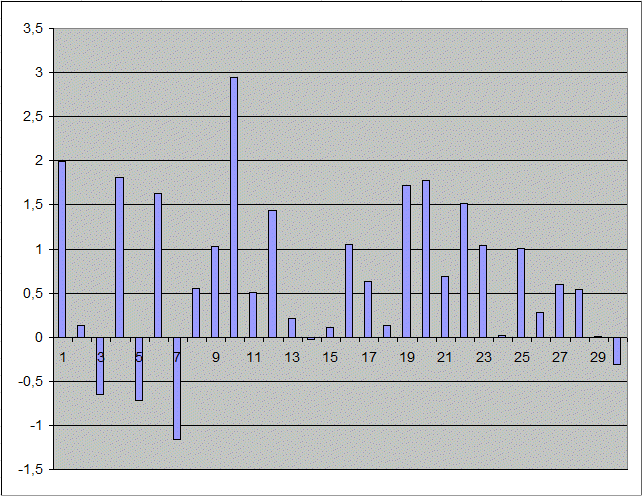
Quand il s'agit de données statistiques, ce graphe qui n'est pas un histogramme, n'a pas une grande utilité pour "voir" les données et leur structure.

En particulier, il donne un rôle peut-être sans signification physique à l'ordre dans lequel sont venues les données.

Renversement des axes x et y et comptage. Pour passer du graphe "naïf" à un histogramme, on inverse les axes x et y.

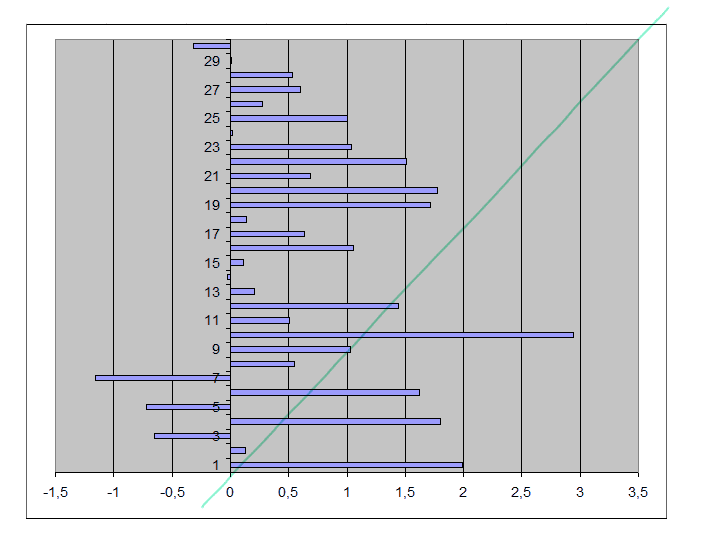
Et on va maintenant compter les données par tranches. (On a encore une fois le choix sur les tranches, mais utilisons celles proposées par le tableur.)

Décomptes. Voici les 9 comptes par tranche (chiffres en rouge sous le dessin) :

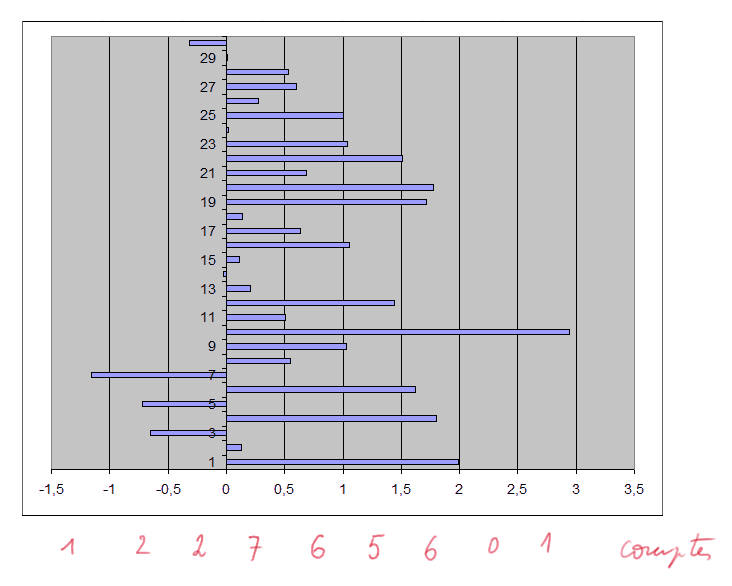
La somme des 9 comptes fait 30.

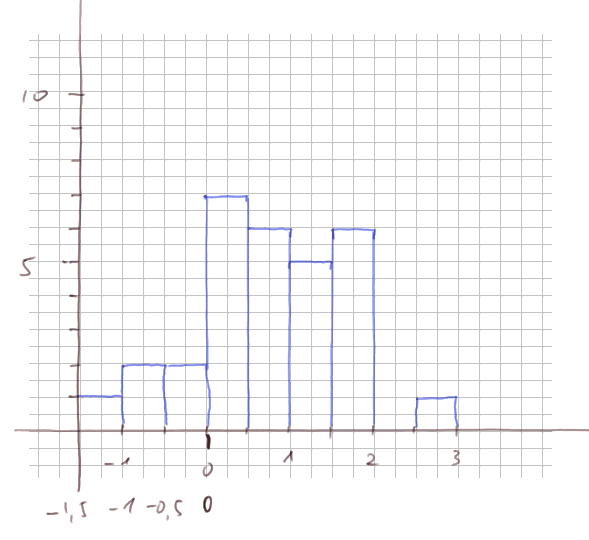
Histogramme dans le deuxième exemple. La représentation de ces neufs comptes donne un histogramme :

Influence du choix des tranches. Comme on l'a dit, quand on veut dessiner l'histogramme d'une série de données statistiques, on a le choix sur les tranches. Quelle largeur choisir ? Quelles bornes choisir ?

Voici les mêmes données statistiques (issues de mesures sur un geyser) avec quatre choix de tranches différents. On a fait varier la finesse des tranches :

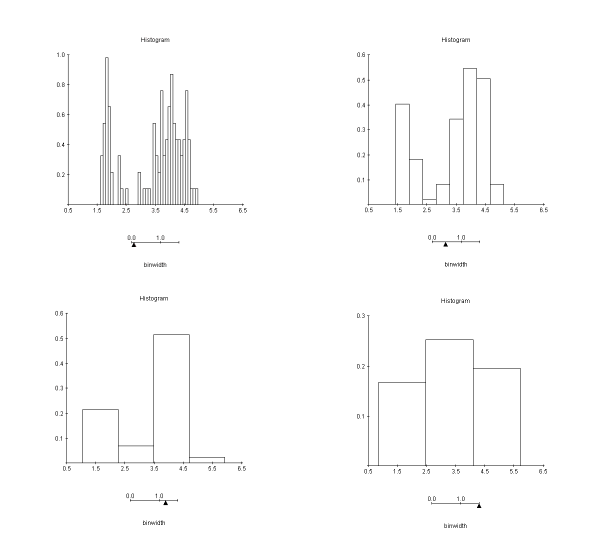
Source : http://www.stat.sc.edu/~west/javahtml/Histogram.html

On voit que l'allure de l'histogramme change. Les trois premiers révèlent deux groupes différents, le quatrième les cache.

Meilleur histogramme. Un esprit mathématicien, confronté à une telle situation, se demandera immédiatement : "Quelle est la largeur de tranche idéale ? (et les bornes idéales ?) " Pour cela il faudrait définir une mesure de la qualité d'un histogramme puis calculer quel histogramme l'optimise.

Tranches de largeur variable : Il y a des gens qui dessinent des histogrammes avec des tranches de largeur variable, mais à part produire des petits problèmes idiots, on ne voit pas bien à quoi ça sert (à moins que ce ne soit pour préparer à l'intégrale de Lebesgue ?).

Exercices :

1. Redessiner l'histogramme de ces données avec des tranches de largeur 1 et pour bornes les nombres entiers relatifs :
   
   
   
   
   
   

Les écrans de la vidéo

écran 1
écran 2
écran 3
écran 4
écran 5
écran 6
écran 7
écran 8
écran 9
écran 10
écran 11
écran 12

Plan général du cours

Contacter le professeur