Finance with a review of accounting
Present value, opportunity cost of capital
Today's topic is "discounting": the financial technique to go from future values to present values of securities or investments. We will learn the concept of "opportunity cost of capital" and topics related to that.
Remember the fundamental idea in Finance: when we make an investment today, either a financial investment or an investment into a project, we want to create future cash flows which have more value than the money we spend today. But this last sentence contains a catch: we don't mean that the future value of the cash flows should be higher than the value invested, we mean that, somehow, the present value of the future cash flow(s) should be higher than the value invested today. When we make our investment, what we receive today is a promise of one sort or another. That's why an investment should be viewed as a transaction today. And it is the value today of this promise we are interested in. So we need to define and compute the present value of a future cash flow or cash flows.
Value creation: if we can spend today a sum of money C0, which will produce a series of cash flows C1, C2, ... , Cm, and the present value of these m future cash flows is higher than C0, we say that we create value today.
The concept of value has puzzled man for centuries. It is surprisingly difficult to pinpoint what is the value of an object or a service. Standard finance offers some explanations, and we shall learn them, but they don't completely solve the question. There is still room for research and new more convincing and more useful theories.
The process of value creation is a puzzling one too. You may ask: "But how come could we receive - from somebody else? - something that has more value today than the price we pay out?". Answer: this situation is fairly common; when a product leaves a firm to be sold, it is exchanged for a price that is usually higher than its value recorded in the stocks. For instance, we may have value in stock 70€, and selling price 100€. So the firm creates value.
The crux of the matter is that the value of an object or a service is not the same for everyone. The object, that is worth 70€ to the firm, is likely to be worth more than 100€ to the customer. And that's precisely why the customer gives out 100€ to receive the product.
Remember the idea of the key to a trunk containing a treasury, which we mentioned when we talked about eBay buying Skype for an astronomical sum. The key - Skype - was worth much more to eBay - which owns the trunk - than to other potential buyers.
Similarly, a toolbox (with hammer, saw, screwdriver, etc.) will be worth more to someone who has the know-how of a carpenter than to someone who doesn't.
A digression on value creation
In Western Europe the pervading culture, coming from Aristotle and Thomas Aquinas, has always said that objects or services have one given value and that's it. It lead to all sorts of contradictions, and hampered economic development. It is those other cultures which understood better the relative character of value, and understood better commerce, which spurred economic development: Lombards, Jews, Protestants. They had a more abstract perception of things than catholic Christians. They understood that value is more productively created via exchange rather than via accumulation. That is why they became bankers and merchants. They were often expelled from Western countries and, each time, it created a dramatic economic and social slow down (Jews expelled from Spain in 1492, Protestants expelled from France in 1685, etc.)
Aristotle (384-322 bc) said many very interesting things, but he also declared that heavier bodies obviously fall faster than lighter ones - even though some elementary reasoning shows it cannot be so (think of a heavy body in the course of its fall, split it into two bodies linked by a tenuous silk cord: will they slow down during their fall ?) And the dominican friar Thomas Aquinas (1225-1274) mixed up what he thought God thought, and observation of nature. The franciscan friar Roger Bacon (1214-1294) is one of the first thinkers of the late middle ages to have insisted on observing nature.
From this little digression, just remember that the concept of value is a bit more complicated than it appears. Let's now turn to what traditional financial theory has to say on it.
Suppose we are in the following situation:
- we have two securities S and T
- they are both of the type which will produce one payment in one year, and that's it
- we know everything about S (price, expected value, risk)
- and, concerning T, we know only the expected value, in one year, and the variability of this value.
- both only have systematic risk (resulting from the variability of the economy) ; that is they have no extra random value that would be added like when throwing a die
We want to compute the price today of T.
S has a future value X, and T has a future value Y. Here are the known figures:
E(X) = 6€, σ(X) = 1,333€, PS = 5€.
E(Y) = 180€, σ(Y) = 40€,
Question: what is the price of T?
PT = ?
Definition: we define the risk pattern of a security S, with future value X, as σ(X)/E(X).
Here is an example of two distributions of future values of securities with the same risk pattern
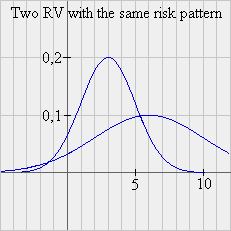
Fact: If two securities have the same risk pattern, they must have the same expected profitability.
Indeed, two securities with the same risk pattern are essentially identical ; they only differ by a rescaling factor.
If they had different profitabilities, this would violate the general "no-arbitrage" principle of finance.
Therefore, if we know the expected value of T in one year, and we know that T has the same risk pattern as S, and we know the profitability of S, then we can compute the price of T. The two prices must verify the following identity:
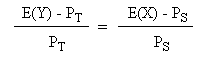
the right part is equal to rS, so this equation is equivalent to
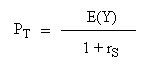
The operation of dividing by (1 + rS) is called "discounting" with rS.
This is a fundamental fact in finance: to compute the price of security T, we must know its future expected value, and we must know the profitability of another security "behaving like T", that is, which has the same risk pattern. Then the price of T is obtained by discounting its expected future value with the profitability of S.
In our numerical example, S and T have the same risk pattern since 1,333 / 6 = 40 / 180. We can say that T "behaves like" 30 securities S. It is the same as "behaving like S". And we know the profitability of S, therefore we can calculate the price, today, of T:
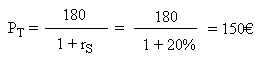
Proof of the fundamental fact (this proof may be skipped):
It is easy to check that any other price for T is impossible ; it would lead to a contradiction. Let's carry out the verification with another price: suppose PT = 160€. Under this hypothesis the security T has the expected profitability
E(RT) = [ E(Y) - 160 ] / 160 = 12,5%
A priori, why not? If the risk of T is also less than the risk of S... And indeed std dev (RT) = std dev { [ E(Y) - 160 ] / 160 } = std dev(Y) / 160 = 40/160 = 25%. So, it looks like such a price for T is OK: "if we pay 160€ for T, we have less average profitability than with S, and we also have less risk..." But it is not OK.
Here is the final stab at the speculation "what about paying PT = 160€ for T?" If indeed we don't like a risk as high as 26,7% (the risk of S), and are ready to give up some profitability to have a lower risk, we can still do better than T. Let's take our 160€ ; let's spend 150€ buying 30 S's ; and we just spare the extra 10€ (we keep them in our pocket). This is like "investing 160€ in a security V".
What is the expected profitability of V? Answer: 30/160 = 18,75%.
What is the risk of V? That is, what is the std dev of the profitability of V? Answer: std dev [ (30*X - 160)/160 ] = (30/160) * std dev(X) = (30/160)*1,333 = 25%
So, if we don't want to go higher than 25% in terms of risk, we don't need to go as low as 12,5% in terms of profitability. We can have a risk of 25%, with a profitability of 18,75%.
Geometric explanation: assuming that we are ready to pay 160€ for T, then we constructed a security V, which combines S and "do nothing", and V is superior to T.
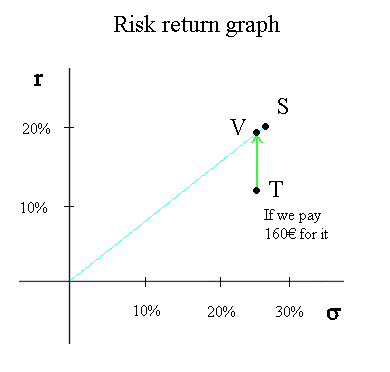
(In fact, we could do even a bit better than V, by lending the extra 10€ to a risk free borrower. But it is not necessary for the proof.)
Conclusion: paying a price of 160€ today for T violates the fundamental principle of Finance. Because there is a better security (V), in terms of profitability, with the same risk. So, the price we should pay for T must be PT = E(value of T in one year) / (1 + rS)
rS is called the opportunity cost of capital of investing into T.
To compute the present value of a security T, we must discount its expected future value with its opportunity cost of capital.
The opportunity cost of capital of investing into a security T is the profitability of another security "behaving like T" in terms of risk.
We call this profitability of the other security "the opportunity cost of capital" of investing into T, because, by investing into T, it is the profitability we give up elsewhere, everything else being equal (namely, with the same risk).
The concept of "opportunity cost of capital" will be generalised to any type of investment (with several cash flows in the future years).
Definition: The opportunity cost of capital of a projected investment is the profitability of a security, traded on the market, which has the same risk pattern as the projected investment.
(We will need to define the risk pattern of a multi cash flow investment.)
And the rule "discount future value with the opportunity cost of capital" will also be generalised to any type of investment: the present value of a stream of future cash flows will be obtained by discounting, in the appropriate manner, each future cash flow. It is the subject of the second half of this lecture.
Question: does the theory expounded so far (randomness of future values, stability of distributions of probability, expected values, profitability, risk return graph, etc.), which is called "the standard financial theory", explain well the behavior of securities in the NYSE (New York Stock Exchange) ?
Answer: not very well. In particular, the bubble and collapse phenomena are not very well modelled by this theory.
A lot of efforts have been spent by thousands and thousands of investors, financial analysts, scholars to try and verify, with real data on securities, if the standard financial theory, which we are in the course of studying, works well. For instance, there are a lot of analyses published by Ibbotson and associates to check how well the theory conforms with and predicts real data. We will spend some time learning them.
Let's think of standard financial theory as a framework of rational tools to approach financial markets as well as investments made by firms. It will help us tremendously to understand the stock market and investments made by firms. It is better than "intuition and pragmatism". But it is not the end answer to how to make good financial and physical investments.
Break time

