Finance with a review of accounting
Opportunity cost of capital and internal rate of return
Discounting a security over one year
In the first half of this lecture, we saw that to compute the price today
of a security T we must discount its expected
value in one year with its
opportunity cost of capital, that is, with the profitability of a known security S
"behaving like T".
(Here we look at securities which will produce only one payment a year after their purchase, and nothing thereafter, and which have only systematic risk coming from the variability of the economy - no extra randomness as from throwing a die to add some value with mean zero.)
The price today of T, noted PT, is also called its present value. Its expected value in one year is often called its future value.
This price PT is such that T and S have the same profitability: rT = rS.
We were, therefore, in a situation where we knew the future value, and the proper discount rate, and we computed the price.
Now let's consider a situation where we know the future value of T as well as its present value (its price today). To stick with standard notation, now PT will be denoted PV(T) and E(Y) will be denoted FV(T). We shall study the function
.gif)
when r varies. This function is called the net present value of T, depending upon r.
With FV(T) = 180, and PV(T) = 150, here is the graph of NPV(T, r) when r varies:
2.gif)
When r = 0, NPV = 30 because, then, it simply is the profit over one year. And when r = 20%, NPV = 0, because r = 20% is the opportunity cost of capital of T, and, therefore, it is the discount rate we used to compute PV(T) is the first place.
All this sounds like playing with words and numbers to state obvious things (including the next fact), but it is important because it will lend itself to a generalisation where it is no longer trite.
Fact: the value of r, such that NPV(T, r) = 0, is the profitability of T.
We may also note this second fact, which will have more meaning as the course unfolds: in the stock market the net present value of any security, which we may buy, is zero. (This is one of the paradoxes of finance: it states that, in theory, there is no way to create value for us by playing in the stock market.)
Now, we are in a position to study investments which will produce a stream of cash flows over several years.
Discounting the future cash flows of an investment
Consider an investment I with the following cash flows: C0 (initial investment today), C1, C2, ... , Cm (future cash flows). The future cash flows are random variables, but, from now on, we refer to their expected values.
Numerical example:
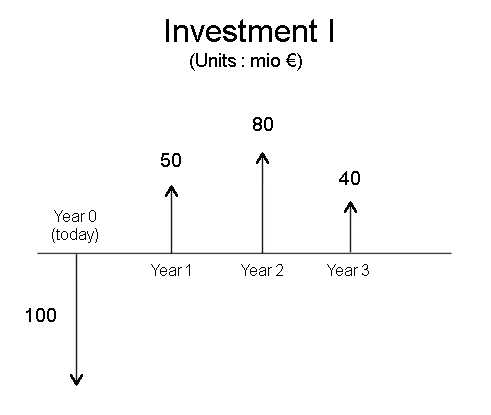
Note that, now, we usually already know what is the amount of money to be spent at the outset. If the future cash flows have a present value higher than C0, then we shall be in a favorable situation.
It is possible to construct a complete, clean probabilistic model of behavior of the future cash flows, and to define the risk pattern of the collection of future cash flows (just like we did for a security over one year). The model is more intricate than for a security.
It is then possible to find an entirely known security S "behaving like the future cash flows of I". Then, the profitability of S is called the opportunity cost of capital of I.
Why this barbaric sounding name? Answer: the idea is that "if we invest into I, we give up the possibility of investing into S, which is equivalent in terms of behavior and financial consequences", therefore "investing into I has an opportunity cost", namely the opportunity to invest into S. So, the profitability of S (the benefit of which we give up) is the opportunity cost of I.
Finally, we can compute the present value of these future cash flows by discounting them with the opportunity cost of capital of I.
We won't go into the mathematics of the model, but will stay at an intuitive level. The present value of C1 will be obtained by discounting it with (1+r). The present value of C2 will be obtained by discounting it with (1+r)2. The present value of C3 will be obtained by discounting it with (1+r)3, etc.
In our numerical example, suppose that the collection of future cash flows of I behaves like the security S which we have already used (E(X) = 6€, σ(X) = 1,333€, PS = 5€, and, therefore, rS = 20%, and risk of S = 26,7%), then the PV (present value) of the future cash flows of I is
1.gif)
computations yield: PV(C1, C2, C3) = 120,37 million euros.
This is a favorable situation: with an investment of 100 mio euros (C0) we can produce a stream of future cash flows which have a present value for us of 120,37 mio euros. In other words, the investment I has a net present value of 20,37 mio euros.
The general formula for the PV (present value) of a series of future cash flows is this (where r is the opportunity cost of the collection of cash flows) :
.gif)
This formula has an interesting interpretation: it transforms each future cash flow Ci into a value today, in order to make them comparable. The "raw" cash flows are not comparable, because they don't correspond to the same years ; but, when each of them is properly discounted, they become comparable: they are, then, expressed in today's money ; they are expressed with their present value.
Differences between one security and an investment
At this point, it is important to stress the similarities and the differences between investing into one security (and selling it one year later) and making an investment into a project which will produce a stream of future cash flows.
Similarities: in both cases, we spend money today, and expect some money in the future. The money or sums of money we shall receive in the future are unsure quantities, so we work with a probabilistic model. We need to know or estimate distributions of probability, means, variances, etc. We did it in the case of a single payoff in one year ; we did not do it in the case of a stream of cash flows, because we need, first, to study several random variables produced in the same experiment E, joint distributions of probability, dependence and independence, etc. And then we need to define clearly what is the risk pattern of a collection of future random cash flows, the present value of a cash flow in two years, etc. So we decided to stay at an intuitive level. If we have the time, later in the course, we will study a little bit two random variables produced in the same experiment.
Differences: concerning a share bought in the stock market, it is an unrealistic situation when we pay a different price for it than its market price. So securities in the stock market have a price which is their present value, and, therefore, their NPV is always zero. Concerning physical investments, things are different. Usually we know how much money we must spend today to produce a stream of future cash flows, and, usually, the initial investment C0 is different from the PV (present value) of the future expected cash flows. Sometimes the NPV is positive - the investment is worth considering ; sometimes the NPV is negative - the investment project must be discarded.
How to find the opportunity cost of capital of an investment?
The theory says "find a security which has the same risk pattern as your investment, then the profitability of that security is your opportunity cost of capital". Fine ! Now, let's plunge and try to swim...
In the most general situation, we shall use the ROCE of firms in the same industry. More precisely, we must figure out the beta of the project (see later), and this will lead to the proper discount rate for the investment cash flows.
If we are the financial officer of a firm and the management considers a new investment project I. For instance, it is the renovation of the warehousing system of the firm ; it will cost $50 mio ; and it will save $12mio after tax every year over the next six years (source: Ross, Westerfield, Jordan, Fundamentals of Corporate Finance, McGraw-Hill/Irwin, 6th edition, 2002, page 494). We are asked the compute its NPV. How do we do it? Answer: if we can consider this project as a "main stream project" in the firm, we will use the so-called Weighted Average Cost of Capital (WACC) of the firm, which is the average cost of capital for the firm when it raises or borrows money on the financial market. (Briefly stated, people putting money into the firm (that ends up recorded on the liability side of the balance sheet) give up other opportunities with the same risk as the firm, therefore, they expect from the firm a cash generation with the same expected profitability. It is called the cost of capital for the firm, and "main stream" investments made by the firm should have at least this profitability, otherwise the investors will turn away from that firm.) More on this later.
Profitability of a stream of cash flows: the IRR
The notion of profitability of a single cash flow E(X) in one year, compared to the price P we pay today (simply enough: r = (E(X) - P)/P ), can be extended to an investment I, with initial cash flow out C0, and which produces a stream of future cash flows C1, C2, C3, ..., Cm.
We cannot just use [C1 + C2 + C3 + ... + Cm - C0] / C0. For instance, with the above numerical example, the "profitabilitiy" of I is not (170 - 100)/100 = 70%.
In fact, we need to define what we mean by "the profitability" of I. This is where the heavy looking manipulations we did with one security come handy. We shall generalise the following fact: the profitability of a security is the value r such that NPV of the security equals zero.
Definition: the "profitability" of an investment I ( C0, C1, C2, C3, ... , Cm) is the value of r such that NPV(I, r) = 0, where:
2.gif)
This "profitability" of I is given a name: it is called the internal rate of return of the investment I.
Numerical example:
Consider, once again, the above investment I (-100, 50, 80, 40). Here is a plot of NPV(I, r):
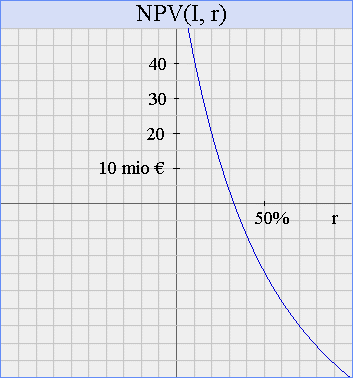
We see that the value of r, for which NPV(I, r) = 0, is slightly above 30%.
There is no simple formula to compute the IRR. One method is trial and error ; another is an interpolation between two values of r and their respective NPV(I, r) ; a third one is the "goal seek" tool of Excel (see the Excel sheet joined to this lecture).
Here, the exact result is IRR = 32,87...%. Notice, however, that in Finance, giving profitability measurements with more than two significant digits is usually meaningless, owing to the fact that we are in a "soft science", not a hard one like Physics. So it is better to just say that the IRR is around 33%.
We can also read from the graph, that, with an opportunity cost of capital is 20%, the NPV of I is just about 20 mio €.
Opportunity cost of capital and IRR
Do not mix up the two concepts. They are close, of course, but they are not the same.
The opportunity cost of capital of an investment is the profitability of a "similar" security. When we discount the investment future cash flows with this r, and subtract the initial payment, we obtain the NPV of the investment.
The opportunity cost of capital of an investment is exogenous: it is a measure obtained from the environment of the investment.
On the contrary, the IRR of an investment is endogenous: it is not obtained from the market or anywhere. It is strictly a function of the various cash flows of the investment itself.
It is the value of r such that NPV(I, r) = 0.
With these two values, we can state the following fact: an investment has a positive NPV if and only if its IRR is higher than its opportunity cost of capital*.
If the IRR of an investment is higher than its opportunity cost of capital, the investment has a positive NPV. It "creates value". It is worth considering.
On the other hand, if the IRR of an investment is lower than its opportunity cost of capital, the investment represents value destruction, and should be discarded.
This is why, often, when evaluating a new projected investment, we first compute its IRR, and if the IRR is "high" we say "the investment is good" (because we implicitly mean: "its IRR is higher than its cost of capital").
Once we get used to all these considerations, they will become straightforward and obvious. They only state formallly things like this: when considering an investment I with IRR 5%, if you also have the possibility to put your money in a security S yielding 8% with the same risk, you won't put your money into I.
* This is true provided NPV is a decreasing function of r. It is possible to construct classroom examples where NPV is a more complicated function of r than simply decreasing. But nowhere do they correspond to real situations.
1) Let's consider the investment: C0=350, C1= 100, C2=200, C3=100. We figure out, from one source or another, that its opportunity cost of capital is 9%. Is it an investment worth considering ?
2) What is its IRR ?

