Cours de mathématiques de 6e15. La division euclidienne |
|
|
|
|
Video |
La "division euclidienne" est le nom officiel de la bonne vieille division des nombres entiers avec un quotient et un reste.
Combien fait 7 divisé par 3 ?
Ça fait 2 et il reste 1. Eh voilà : nous avons fait une division euclidienne !
À vous de jouer :
Voici un nombre noté non pas avec les chiffres arabes mais "à l'ancienne" avec des petits cailloux.

Appelons ce nombre, N.
Sauriez-vous faire la division euclidienne de N par quatre ?
Faisons-la ensemble : la question est "combien de fois quatre petits cailloux tiennent dans le nombre N, et combien en reste-t-il à la fin après qu'on a enlevé tous les paquets de quatre ?"
Commençons par ranger les cailloux par groupes de quatre. Si on fait par exemple des colonnes avec les paquets de quatre, ça donne la configuration suivante :

Maintenant on voit qu'on peut enlever cinq paquets de quatre petits cailloux, et il en restera encore trois (dont on ne peut plus enlever un paquet de quatre évidemment).
Donc le résultat est
N = cinq fois quatre plus trois
Bien sûr, on peut noter tout cela avec les chiffres arabes. N, vous l'aviez reconnu, est le nombre aussi noté 23.
Et la division ci-dessus s'écrit
23 = 5 x 4 + 3
Mais il est important de comprendre que les nombres viennent avant leurs notations et même avant leurs noms. De même, vous existiez avant qu'on ait pris une photo de vous, ou qu'on ait enregistré pour vous un prénom et un nom à la mairie.
La division de N par quatre n'a rien à voir avec les diverses notations possibles des nombres qui interviennent dans le calcul. C'est pour cela que nous avons tout d'abord choisi de vous la proposer avec des petits cailloux.
Une division euclidienne ce n'est pas plus compliqué que ça !
Les chiffres arabes (qui sont en réalité d'origine indienne, apparus durant le premier millénaire avant Jésus-Christ) sont géniaux pour la raison suivante :
On vient de voir qu'on peut parfaitement faire des calculs avec des petits cailloux. On peut même faire des calculs avec des petits cailloux "en système à base dix". Voici comment on procède :
On a une planchette inclinée avec plusieurs rainures dans lesquelles on peut mettre des billes
Le nombre vingt-quatre représenté avec des billes comptant pour des unités et des billes comptant pour des dizaines.
Il s'agit donc d'une représentation "en système à base dix".
Sauriez-vous faire des calculs "en système à base 7" ?
Au départ on travaille seulement dans la rainure des unités, c'est-à-dire, par convention, celle la plus à droite. Si on veut additionner trois et un, on commence par mettre trois billes dans la rainure, puis on en rajoute une, et on compte : on en a quatre. Parfait ! C'est le résultat de l'addition.
L'astuce c'est que dans la rainure des unités dès qu'on a dix billes ou plus, on en enlève dix et on met une bille dans la colonne des dizaines. Et – comme si on jouait à la marchande – "on dit que" les billes dans la colonne des dizaines "valent" dix billes normales (c.-à-d. de la colonne des unités). Pour l'instant ce n'est pas bien sorcier.
Ainsi dans le dessin ci-dessus, on a une configuration de billes représentant le nombre vingt-quatre.
Le génie des chiffres arabo-indous est ensuite d'avoir remplacé les paquets de billes de zéro à neuf, par dix signes arbitraires.
les chiffres arabes n'ont pas la même forme partout :
plaque minéralogique libanaise (source : wikipedia)
Ces signes ne sont pas les mêmes partout dans le monde. Ceux utilisés de nos jours dans le monde occidental sont présentés ci-dessous. L'image à droite montre les chiffres arabes utilisés au Liban.
| une bille est désormais notée | 1 |
| deux billes sont notées | 2 |
| trois billes sont notées | 3 |
| quatre billes sont notées | 4 |
| cinq billes sont notées | 5 |
| ... | ... |
| neuf billes sont notées | 9 |
| et même, zéro bille est noté | 0 |
Alors le nombre ci-dessus n'est plus représenté avec des billes, mais seulement avec nos nouveaux symboles. Le nombre vingt-quatre est maintenant noté 24.
Ça a l'air évident et sans sophistication particulière, mais c'est seulement parce qu'on est tellement habitué à cette manière de procéder qu'on ne voit plus son caractère génial.
Ça ne résout pas tous les problèmes de calculs. Mais ça les simplifie à l'aide d' "algorithmes". Un algorithme est une façon mécanique et répétitive de faire quelque chose.

trois mille deux cent vingt sept fois deux
Pour faire des additions ou des multiplications il faut encore connaître sa table d'addition ou sa table de multiplication. Il faut bien le noter : les chiffres arabes ne créent pas de "table de multiplication automatique". Ils ne dispensent pas de connaître sa table de multiplication. Mais ensuite ils rendent relativement simple de faire une multiplication (cf. la leçon sur la multiplication) alors que ça ne l'était pas, par exemple, avec les chiffres romains.
Et avec les petits cailloux sans la tablette rainurée c'est rapidement incommode. Essayez de montrer à vos enfants comment multiplier trois mille deux cent vingt sept par trois à l'aide de dix mille petits cailloux. Ils seront déjà lassés quand vous aurez à peine compté le premier paquet.
Avec la tablette rainurée, c'est beaucoup plus facile, – d'ailleurs nous vous encourageons vivement à le faire pour comprendre vraiment comment marchent deux additions – mais ça reste quand même fastidieux par rapport à l'emploi des symboles 0, 1, 2, 3 4, 5, 6, 7, 8 et 9.
Faisons maintenant la division de N par trois.
Enlevons des paquets de trois cailloux les uns après les autres comme dans les jeux où il faut reconnaître des mots dans une grille remplie de lettres :
Visionnez le film pour voir les paquets de trois qu'on enlève.
On a enlevé sept paquets de trois, et il reste encore deux cailloux.
Donc on peut écrire :
N = sept fois trois plus deux
ou encore
23 = 7 x 3 + 2
Si on se rappelait que 3 x 7 = 21, on pouvait faire tout de suite la division euclidienne dans sa tête.
Il est très important de connaître sa table de multiplication par coeur !
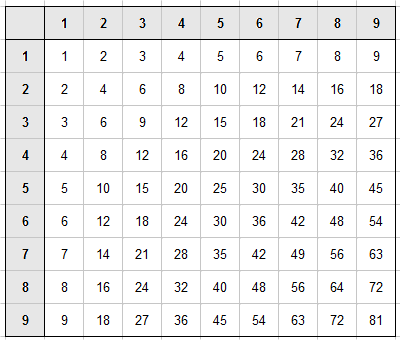
Table de mutiplication
Voici une page pour vous aider à réviser si nécessaire.
Quand on ne connaît pas sa table de multiplication, le monde est un endroit plus flou, plus vague, plus mystérieux. Tandis que quand on la connaît bien, par coeur, il est beaucoup plus facile à comprendre, et il est plus facile de s'y repérer.
Avec les fractions, par exemple, on est parfois amené à chercher des quantités comme 2/5 de 17,5 mètres. Si on ne connaît pas sa table de multiplication, on n'a a priori pas beaucoup d'idée de la longueur que ça peut représenter. En revanche si on la connaît bien, on voit tout de suite que cette longueur est 7 mètres.
Faisons une division euclidienne avec des nombres plus grands.
Quelle est la division euclidienne de 2012 par 67 ?
On peut poser la division comme on l'a appris ici.
Mais - sous réserve que vous connaissiez bien votre table de multiplication - il n'est pas interdit d'utiliser sa calculette.
Quand je divise 2012 par 67, ma calculette me donne comme résultat : 30,0298507... C'est-à-dire que 67 tient trente fois dans 2012 et il y reste encore un peu (mais moins que 67).
Effectivement, 67 x 30 = 2010.
Donc la division euclidienne de 2012 par 67 est
2012 = 30 x 67 + 2
D'une manière générale, on a deux nombres, appelons-les a et b (où b est plus petit ou égal à a). On cherche combien de fois on peut "mettre b" dans a. Et quel est le reste (forcément strictement plus petit que b) ?
Exemple : la division euclidienne de 127 par 35. Combien de fois 35 tient dans 127 ? Essayons 2 fois : 2 x 35 = 70, reste 57. On peut encore "mettre 35" une fois dans le reste de 57. Il restera alors 57 - 35 = 22. Donc 127 = 3 x 35 + 22.
On a déjà révisé, dans la leçon "poser et effectuer une division", comment faire une grosse division. Refaisons-en une (voir video pour la mécanique de calcul) : 13419 divisé par 437 égale 30 et il reste 309.
Division euclidienne et notation avec les chiffres arabes :
Le système de notation des nombres avec les chiffres arabes est très lié à la division euclidienne par 10, 100, 1000, etc. Prenons le nombre DCCLXXIII, écrit en chiffres romains pour ne pas dès le départ l'écrire en chiffres arabes, puisque c'est précisément l'objet du paragraphe de montrer comment on fait. Combien de fois mille tient dans DCCLXXIII ? Zéro fois. Combien de fois cent tient dans DCCLXXIII ? Sept fois. Et il reste LXXIII. Combien de fois dix tient dans LXXIII ? Sept fois aussi, et il reste III. Alors on écrit le nombre DCCLXXIII sous la forme 773 : ça veut dire que DCCLXXIII = 7 x 100 + 7 x 10 + 3.
Les nombres en notation arabe sont déjà en quelque sorte le résultat d'une série de divisions euclidiennes, par 10, 100, 1000 etc. Mais on commence par le nombre 10...0 le plus grand possible. On voit combien de fois il tient dans le nombre qu'on veut représenter. C'est forcément un quotient entre 1 et 9, car sinon on aurait pu aller au nombre 10.....0 avec un zéro de plus. Puis il y a un reste. On le divise par le nombre 10...0 avec un zéro de moins. Il y a un reste. Et ainsi de suite, jusqu'à division par 10 du dernier reste précédent qui était entre 0 et 99. Et le dernier reste est entre 0 et 9.
Nos dernières traductions
Le cadeau idéal à quelqu'un qui veut comprendre la physique
 |
 |
|
| Ni manuel scolaire, ni ouvrage de vulgarisation, une présentation simple et claire des concepts et outils de la physique classique par Leonard Susskind (niveau : baccalauréat scientifique). | La mécanique quantique présentée avec le même didactisme remarquable qui a rendu les ouvrages de Leonard Susskind célèbres auprès d'un vaste public (niveau : baccalauréat scientifique). | |
| L'émission CQFD parlant du livre à la Radio Suisse le 1er septembre 2015. |

Plan général du cours
Contacter le professeur
Révise aussi ton anglais avec des tests très simples.
